Если вы думаете, что логарифмы, линейное программирование и криптография никак не касаются вашей жизни, то глубоко заблуждаетесь.
Лайфхакер задался вопросом, какое значение математика имеет в нашей повседневной жизни. Разве она вообще кому-то ещё нужна? Ответ на этот вопрос нашёлся в книге Нелли Литвак и Андрея Райгородского «Кому нужна математика? Понятная книга о том, как устроен цифровой мир».
О чём эта книга?
О математике. 🙂 Точнее, о тех её разделах, которые больше всего востребованы в логистике, транспортных расписаниях, шифровании и кодировании данных. Авторы на доступных примерах показывают, как математика помогает экономить время и деньги, сохранять ваши данные под надёжной защитой и выбирать очередь в магазине.
Что такое линейное программирование
В данном случае речь не идёт о программировании как таковом. Это скорее процесс оптимизации. Почему линейное? Потому что речь идёт только о линейных уравнениях: когда переменные складывают, вычитают или умножают на число. Никаких возведений в степень или перемножений. Такое программирование помогает минимизировать стоимость товаров или услуг (если мы говорим о торговле) или увеличить доход.
Линейное программирование используется в нефтяной индустрии, а также в сфере логистики, планирования, составления расписаний.
Если коротко, то на примере это выглядит так.
Вообразим, что вы занимаетесь продажей жестяных листов. Один клиент заказал у вас 70 листов, а второй — 30 листов. При этом ваши запасы хранятся на разных складах, на каждом из которых осталось меньше 100 листов. Ваша задача — минимизировать расходы на доставку жести клиентам.
Вот тут и вступает в игру линейное уравнение. Мы не станем подробно рассказывать, как решается эта задача в книге, но после нескольких этапов вычислений находится наиболее оптимальный вариант, который позволяет сэкономить 12% стоимости доставки в сравнении с расходами, которые пришлось бы понести, если не использовать математический подход.
А теперь представьте, что речь идёт не о доставке нескольких листов жести, а о большегрузах и расписании движения железнодорожного транспорта целой страны. И тут 12% — это уже число с несколькими нулями на конце.
Почему оптимальные решения не всегда самые комфортные?
Математика — наука точная и красивая. Однако не всегда решение задач кажется нам достаточно подходящим. Так случилось с расписанием железнодорожного транспорта Нидерландов. В этой небольшой стране поезда и электрички очень популярны. При этом транспортное расписание настолько устарело, что вот-вот должен был произойти настоящий коллапс.
Поэтому в 2002 году было принято решение составить новое расписание. Экспертам нужно было идеально продумать количество вагонов, время остановок, прибытия и отправления, не говоря о расписании машинистов и кондукторов для 5 500 поездов в день.
В итоге было составлено идеальное с математической точки зрения расписание. И вроде бы все должны быть довольны. Но только не пассажиры: остановки слишком короткие, вагоны чересчур загружены, никакого комфорта. Так случилось потому, что математики решают только математические задачи. И кто виной тому, что хромает менеджмент?
Можно ли закодировать всё что угодно?
Обычному пользователю компьютера сложно вообразить, что все картинки, видео, тексты, песни — это не картинки, видео, тексты и песни, а нули и единицы, единицы и нули.
Закодировать текст легче всего: для каждой буквы, цифры или знака препинания придумать свою последовательность единиц и нулей. А вот как быть с цветом? К счастью, физики узнали, что каждый цвет — это сочетание красного, синего и зелёного. А значит, и цвета можно превратить в цифры.
У каждого цвета есть 255 оттенков. Например, оранжевый — это 255 красного и 128 зелёного, голубой — 191 зелёного и 255 синего. А раз цвет можно представить цифрами, значит, его можно поместить в любой компьютер, телевизор или телефон.
С видео ещё сложнее — слишком много информации. Однако математики нашли выход и из этой ситуации и научились сжимать данные. Первый кадр фильма кодируется полностью, а затем кодируются только изменения.
Проблемы остались только с музыкой. Учёные до сих пор не научились кодировать музыку так, чтобы она звучала настолько чётко, как в жизни. Потому что музыку нельзя разложить на «оттенки», которые можно было бы записать в цифровом представлении.
Почему интернет никогда не ломается?
Нет, сейчас не о работе ваших провайдеров, которая иногда могла бы быть лучше. Речь о том, почему, к примеру, Google всегда отвечает на наши запросы, почему мы всегда можем получить доступ к нужным сайтам, и о том, почему помехи (а их на самом деле много) не отрезают нам доступ к Всемирной паутине.
Короткий вариант ответа на этот вопрос такой: в середине прошлого века два математика Пол Эрдеш и Альфред Реньи открыли миру случайные графы. Графы — это изображение узлов, соединённых линиями. Так вот, представим, что узлы — это компьютеры, а линии — каналы связи. Если взять граф для 100 компьютеров, выглядеть это будет вот так:
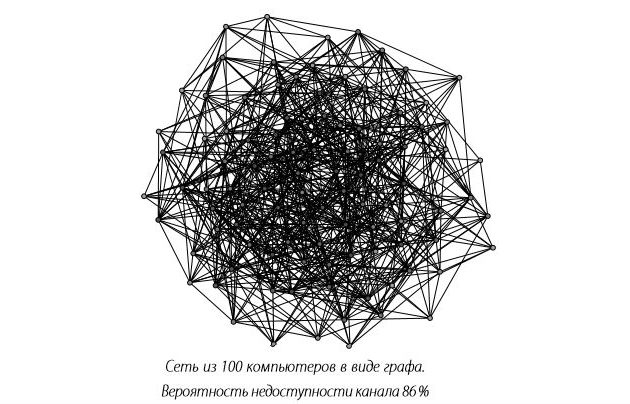
И вот Реньи и Эрдаш путём сложных для гуманитариев и простых для технарей вычислений пришли к ошеломительному выводу. Чем больше в сети компьютеров, чем больше между ними связей, тем меньше вероятность критической помехи, то есть такой, которая оторвёт нас от мира безграничного общения и бесконечной информации.
Если не верите, вот вам таблица.
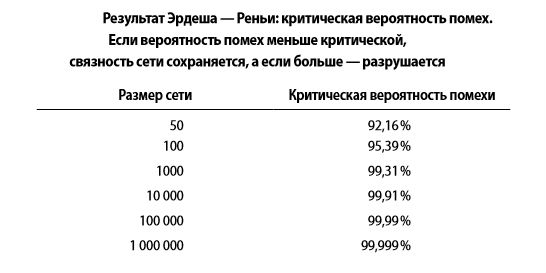
То есть, если какой-то канал нарушен, практически всегда остаётся возможность пойти по другому каналу и связаться с нужным сервером.
Что такое очередь в интернете и как её избежать?
Вы знали, что каждый раз, задавая вопрос Google или отправляясь на какой-либо сайт, вы попадаете в очередь? Конечно, она движется намного быстрее, чем на кассе в супермаркете, и вы практически не замечаете простоя, но тем не менее, если кто-то совершил слишком глобальный запрос, потребуется больше времени на его обработку.
Поэтому нужно выбрать сервер, в котором очередь самая маленькая, или тот, в очереди к которому нет тяжеловесного запроса.
И тут вступает в силу правило выбора из двух. Информатики Дерек Игер, Эдвард Лазовска и Джон Захорджан в 1986 году предложили и доказали теорию о том, что если ограничить выбор серверов, на которые будет отправлен ваш запрос, до двух, то вероятность проскочить очередь увеличится в разы.
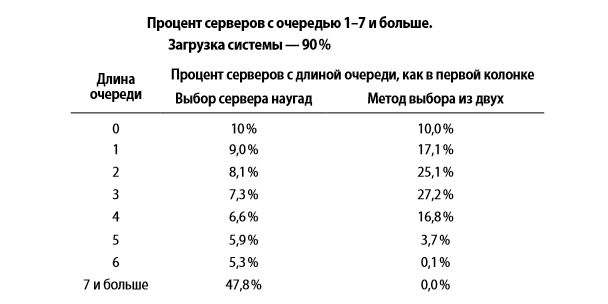
Давайте рассмотрим это на примере супермаркета. Перед вами множество касс с разной длиной очереди. У вас есть варианты: случайно выбрать первую попавшуюся или остановиться на двух и выбрать ту, в которой очередь меньше. Так вы с большей вероятностью завершите покупки быстрее.
Теория четырёх рукопожатий
Многие слышали о том, что все люди в мире знакомы между собой через шесть рукопожатий. Эту теорию ещё в 1960-х доказал социолог Стэнли Милграм, попросив людей из разных штатов отправить письмо одному человеку. Письмо нужно было сначала отправить своему знакомому, тот, в свою очередь, отправлял своему — и так, пока письмо не дошло до адресата. В итоге цепь составила всего шесть человек.
Так было до тех пор, пока сотрудники Facebook не обратились к учёным, чтобы ещё раз подтвердить или опровергнуть эту теорию. Обработав все возможные пары знакомств между всеми пользователями Сети, оказалось, что эта цепь ещё короче. И составляет всего 4,7! Вы можете это вообразить? Между любым человеком на Земле и вами всего 4,7 рукопожатия!
Стоит ли читать эту книгу?
Да, если вы также хотите узнать, как работает шифрование данных, кто взломал шифр «Энигмы», как проходят рекламные аукционы в Google и «Яндексе», а также глубже окунуться в мир математических задач и уравнений.
Лайфхакер рассказал вам далеко не все интересные факты из занимательной математики, поэтому, если вы хотите дополнить свои знания в этой области, книга «Кому нужна математика» наверняка окажется для вас полезной.
Несмотря на простоту изложения, если вы гуманитарий, во время прочтения вам может понадобиться математический справочник.
Источник
