Информационная энтропия хаоса

16.04.2019

Введение

На Habr достаточно много публикаций, в которых рассматривается понятие энтропии, вот только некоторые из них [1÷5]. Публикации были позитивно восприняты читателями и вызвали большой интерес. Достаточно привести определение энтропии, которое дал автор публикации [1]: «энтропия — это то, как много информации вам не известно о системе». Публикаций о явлении хаосе на Habr тоже достаточно [6÷9]. Однако связь энтропии и хаоса в обеих группах публикаций не рассматривалась.

Это объясняется тем, что различные области знаний выделяют разные виды меры хаоса:
• информационная;
• термодинамическая;
• дифференциальная;
• культурная.

Также описываются меры хаоса с учётом их специфики даже в одной из указанных областей довольно сложно.

Пробуя предельно упростить задачу, я решил рассмотреть связь информационной энтропии и хаоса на примере сходства областей прохождения от порядка к хаосу на диаграммах в виде точечных отображений и на графиках энтропийного коэффициента для этих областей.

Что из этого получилось Вы узнаете заглянув под кат.

Механизмы перехода от порядка к хаосу

Анализ механизмов перехода от порядка к хаосу в реальных системах и различных моделях выявил универсальность относительно немногих сценариев перехода к хаосу. Переход к хаосу может быть представлен в виде диаграммы бифуркаций (термин «бифуркация» употребляется для обозначения качественных перестроек системы c возникновением нового режима её поведения).

Вхождение системы в непредсказуемый режим описывается каскадом бифуркаций, следующих одна за другой. Каскад бифуркаций ведет последовательно к появлению выбора между двумя решениями, затем четырьмя и так далее, система начинает колебаться в хаотическом, турбулентном режиме последовательного удвоения количества возможных значений.

Будем рассматривать бифуркации удвоения периода и появление хаоса в точечных отображениях. Отображение – это функция, которая показывает зависимость последующих значений параметров системы от предыдущих значений:

$x_{n+1}=f(x_{n})=lambda x_{n}(1-x_{n})$ .

Рассмотрим также и вторую часто применяемую функцию:

$x_{n+1}=f(x_{n})=lambda cdot x_{n}cdot (1-x_{n}^{2})$ .

C помощью точечных отображений изучают объекты не с непрерывным, а с дискретным временем. При переходе к отображению размерность изучаемой системы может уменьшаться.

При изменении внешнего параметра lambda точечные отображения демонстрируют довольно сложное поведение, которое становится хаотическим при достаточно больших lambda. Хаос это очень быстрое разбегание траекторий в фазовом пространстве.

Бифуркация–это качественная перестройка картины движения. Значения управляющего параметра, при которых происходят бифуркации, называются критическими или бифуркационными значениями.

Для построения диаграмм будем применять следующие два листинга:

№1. Для функции: $x_{n+1}=f(x_{n})=lambda x_{n}(1-x_{n})$ :

Листинг программы

# -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0):         x1=(a-1)/a#точка пересечения функции с прямой                 def ff(x):#логистическая функция                 return a*x*(1-x)            def fl(x):                 return x         x=x0;y=0;Y=[];X=[]         for i in arange(1,1000,1):                 X.append(x)                 Y.append(y)                 y=ff(x)                 X.append(x)                 Y.append(y)                 x=y         plt.title('Диаграмма логистической функции n $x_{n+1}=lambda cdot x_{n}cdot (1-x_{n})$ при $lambda$ =%s и x0=%s '%(a,x0))                plt.plot(X,Y,'r')         x1=arange(0,1,0.001)         y1=[ff(x) for x in x1]         y2=[fl(x) for x in x1]         plt.plot(x1,y1,'b')         plt.plot(x1,y2,'g')         plt.grid(True)         plt.show()

№ 2. Для функции $x_{n+1}=f(x_{n})=lambda cdot x_{n}cdot (1-x_{n}^{2})$ :

Листинг программы

# -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0):         x1=((a-1)/a)**0.5         def ff(x):#логистическая функция                 return a*x*(1-x**2)           def fl(x):                 return x         x=x0;y=0;Y=[];X=[]         for i in arange(1,1000,1):                 X.append(x)                 Y.append(y)                 y=ff(x)                 X.append(x)                 Y.append(y)                 x=y                  plt.title('Диаграмма логистической функции n $x_{n+1}=lambda cdot x_{n}cdot (1-x_{n}^{2})$ при $lambda$ =%s и x0=%s '%(a,x0))         plt.plot(X,Y,'r')         x1=arange(0,1,0.001)         y1=[ff(x) for x in x1]         y2=[fl(x) for x in x1]         plt.plot(x1,y1,'b')         plt.plot(x1,y2,'g')         plt.grid(True)         plt.show()

Для оценки влияния характера логистической функции на критические значения $inline$ рассмотрим диаграммы с функцией $x_{n+1}=f(x_{n})=lambda x_{n}(1-x_{n})$ , для этого будем применять листинг №1:

При 0< lambda <1 для $inline$ и x0=0,47 получим диаграмму:

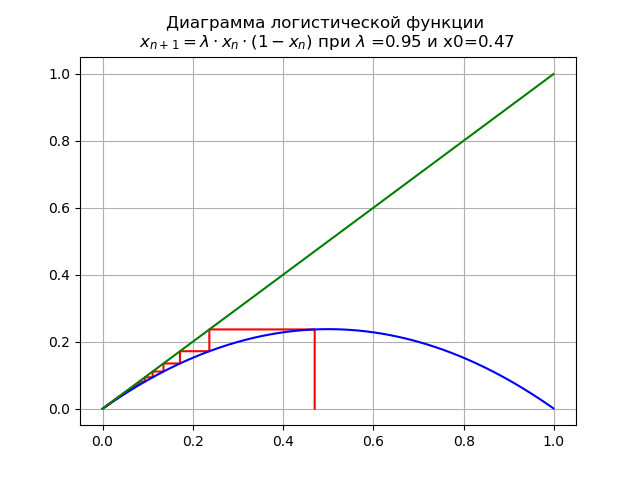
В этом случае отображение имеет единственную неподвижную точку $x^{*}=0$ ,
которая является устойчивой.

При $inline$ для $inline$ x0=0,7 получим диаграмму:

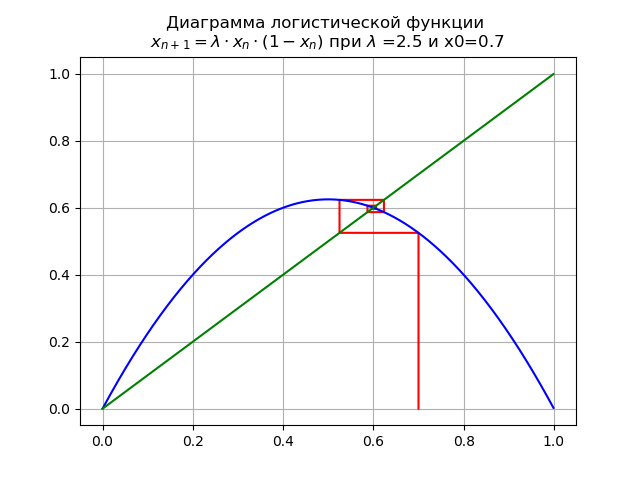
На отрезке [0, 1] появляется еще одна неподвижная устойчивая точка $x_{1}^{*}= 1-1/lambda$

При $inline$ для $inline$ и x0=0,01 получим диаграмму:

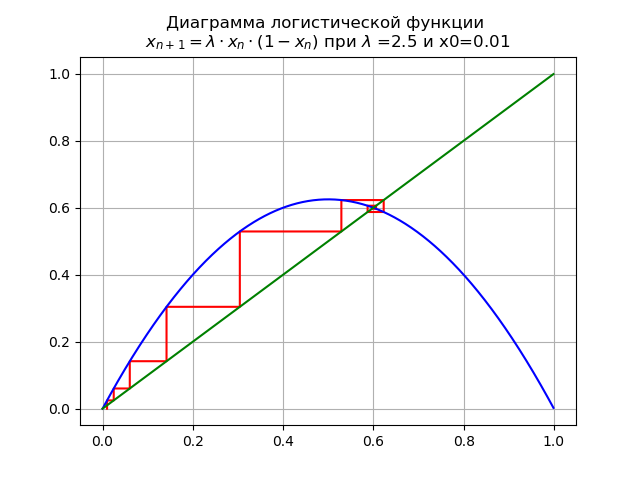
Неподвижная точка $x^{*}=0$ , теряет устойчивость.

При $inline$ для $inline$ и x0=0,7 получим диаграмму:

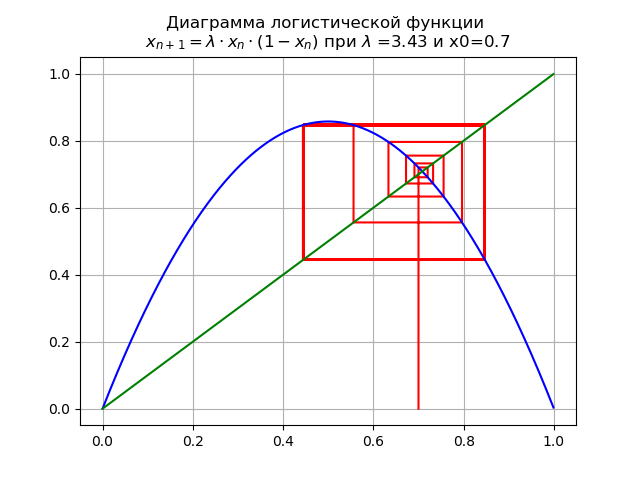
Отображение претерпевает бифуркацию: неподвижная точка $x_{1}^{*}$ становится неустойчивой, и вместо нее появляется двукратный цикл.

При $inline$ для $inline$
и x0=0,2 получим диаграмму:

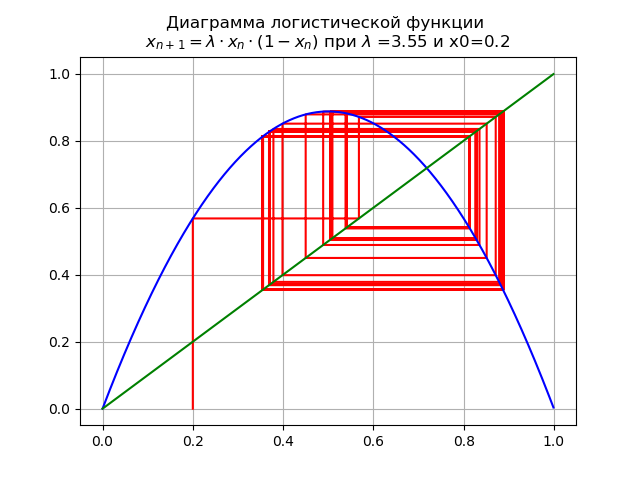
При переходе параметра $inline$ через значение $inline$ , 2-кратный цикл становится 4-кратным, и далее.

При конечном значении $inline$ в системе имеются неустойчивые циклы всех возможных порядков:

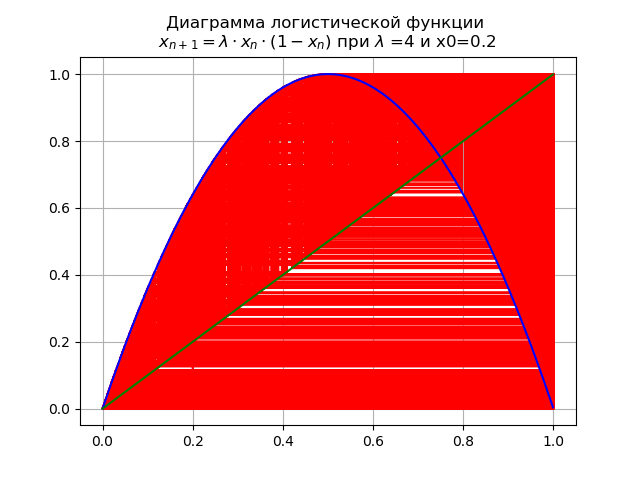
Для оценки влияния характера логистической функции на критические значения $inline$ рассмотрим диаграммы с функцией $x_{n+1}=f(x_{n})=lambda cdot x_{n}cdot (1-x_{n}^{2})$ , для этого будем применять листинг №2.

При $inline$ для $inline$ и x0=0,2:

Отображение имеет единственную неподвижную точку $x^{*}=0$ , которая является устойчивой.

При $inline$ для $inline$ и x0=0,55:

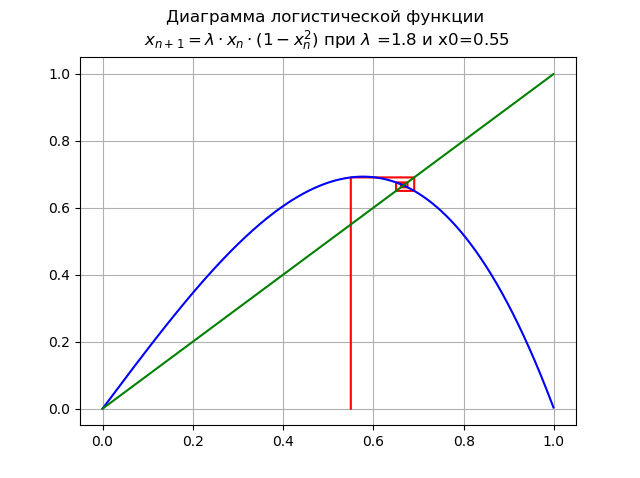
Точка $x^{*}= 0$ теряет устойчивость, появляется новая устойчивая точка $x_{1}^{*}$

При $inline$ для $inline$ и x0=0,2:

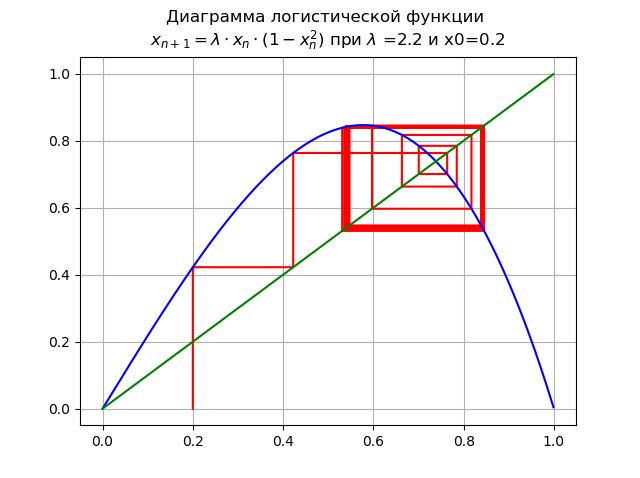
Происходит бифуркация удвоения периода, появляется 2-кратный цикл. Дальнейшее увеличение $inline$ ведет к каскаду бифуркаций удвоения периода.

При $inline$ для $inline$ и x0=0,2:

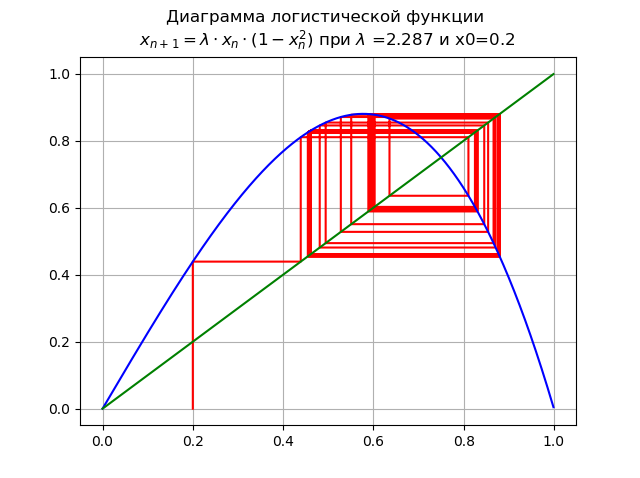
Увеличение $inline$ привело к каскаду бифуркаций удвоения периода.

При $inline$ в системе имеются неустойчивые циклы всех возможных периодов:

Как было показано на диаграммах, с ростом порядка логистической функции диапазон изменения $inline$ сужается.

При помощи диаграмм мы проследили путь от порядка к хаосу, задавая при этом значения $inline$ для разных логистических функций. Остаётся ответить на вопрос: как измерять хаос? Ответ для некоторых из перечисленных в начале статьи типов хаоса известен
– энтропия мера хаоса. Этот ответ в полной мере можно отнести и к информационному хаосу, однако какую энтропию здесь применить и как сравнить с уже рассмотренным численным значением $inline$ — на этот вопрос я попытаюсь ответить в следующей части статьи.

Информационная энтропия и энтропийный коэффициент

Мы будем рассматривать информационную двоичную энтропию для независимых случайных событий $inline$ c $inline$ возможными состояниями, распределёнными с вероятностями $p_{i}(i=1,..,n)$ . Информационная двоичная энтропия рассчитывается по формуле:

$H(x)=-sum_{i=1}^{n}p_{i}cdot log_{2}(p_{i})$

Эта величина также называется средней энтропией сообщения. Величина $H_{i}=-log_{2}(p_{i})$ называется частной энтропией, характеризующей только i-e состояние. В общем случае основание логарифма в определении энтропии может быть любым, большим 1; его выбор определяет единицу измерения энтропии.

Мы будем использовать десятичные логарифмы, при которых энтропия и информация измеряется в битах. Количество информации в битах будет вычисляться правильно, когда, например, переменные $inline$ и $inline$ будут подставляться в соответствующие выражения для энтропии безразлично в каких, но обязательно в одних и тех же единицах. Действительно:

$q=H(x)-H(Delta)=log_{10}left ( X_{2}-X_{1} right)-log_{10}(2Delta )=log_{10}(frac{X_{2}-X_{1}}{2Delta })$ ,

где X и $inline$ должны быть в одних и тех же единицах.

Оценка энтропийного значения случайной величины по экспериментальным данным находится по гистограмме из следующего соотношения:

$Delta_{e}= frac{1}{2}e^{H(x)}=frac{d}{2}prod_{i=1}^{m}(frac{n}{n_{i}})^{frac{n_{i}}{n}}=frac{dn}{2}10^{-frac{1}{n}}sum_{i=1}^{m}n_{i}log_{10}(n_{i})$

где: $inline$ –ширина каждого столбца гистограммы; $inline$ — количество столбцов; $inline$ -общее количество данных; $n_{i}$ — количество данных в $inline$ -том столбце.

Энтропийный коэффициент определиться из соотношения:

$k_{e}=frac{Delta_{e}}{sigma}$

где: $inline$ – среднеквадратичное отклонение.

Информационная энтропия как мера хаоса

Для анализа явлений информационного хаоса используя энтропийный коэффициент, вначале создадим диаграмму ветвления для функции $x_{n+1}=f(x_{n})=lambda x_{n}(1-x_{n})$ с нанесением переходных областей, полученных при построении гистограмм:

Диаграмма ветвления

import matplotlib.pyplot as plt import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(3.58,3.9,0.0001):       for n in arange(1,N,1):                y.append(round(r*y[n-1]*(1-y[n-1]),4))      y=y[N-250:N]     x=[r ]*250     plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1)  plt.figure(1) plt.title("Диаграмма ветвления  при 3,6<= $lambda$ <=3,9") plt.xlabel("r") plt.ylabel("$lambda$ ") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.show()

Получим:

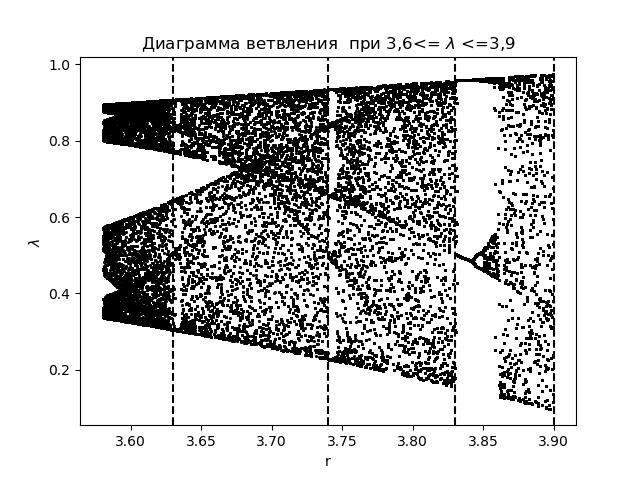
Построим график для энтропийного коэффициента при тех же областях $inline$ :

График для энтропийного коэффициента

import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(3.58,3.9,0.0001):     q=[round(p,2)]         M=zeros([1001,1])         for j in arange(0,1,1):         M[0,j]=0.5     for j in arange(0,1,1):         for i in arange(1,1001,1):             M[i,j]=q[j]*M[i-1,j]*(1-M[i-1,j])                a=[]        for i in arange(0,1001,1):         a.append(M[i,0])     n=len(a)     z=histogram(a, bins=m)     if type(m) is str:         m=len(z[0])         y=z[0]             d=z[1][1]-z[1][0]     h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)     ke=round(h/std(a),3)     data_k.append(ke) plt.title("Энтропийный коэффициент ke для 3,6<= $lambda$ <=3,9") plt.plot(arange(3.58,3.9,0.0001),data_k) plt.xlabel("$lambda$ ") plt.ylabel("ke") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.grid() plt.show()

Получим:

Сравнивая диаграмму и график, видим идентичное отображение областей на диаграмме и на графике для энтропийного коэффициента для функции $x_{n+1}=f(x_{n})=lambda x_{n}(1-x_{n})$ .

Для дальнейшего анализа явлений информационного хаоса с использованием энтропийного коэффициента, создадим диаграмму ветвления для логистической функции: $x_{n+1}=f(x_{n})=lambda cdot x_{n}cdot (1-x_{n}^{2})$ с нанесением переходных областей:

Диаграмма ветвления

import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(2.25,2.56,0.0001):       for n in arange(1,N,1):                y.append(round(r*y[n-1]*(1-(y[n-1])**2),4))      y=y[N-250:N]     x=[r ]*250     plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1)  plt.figure(1) plt.title("Диаграмма ветвления  при 2.25<=$lambda$ <=2.56") plt.xlabel("$lambda$ ") plt.ylabel("y") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.show()

Получим:

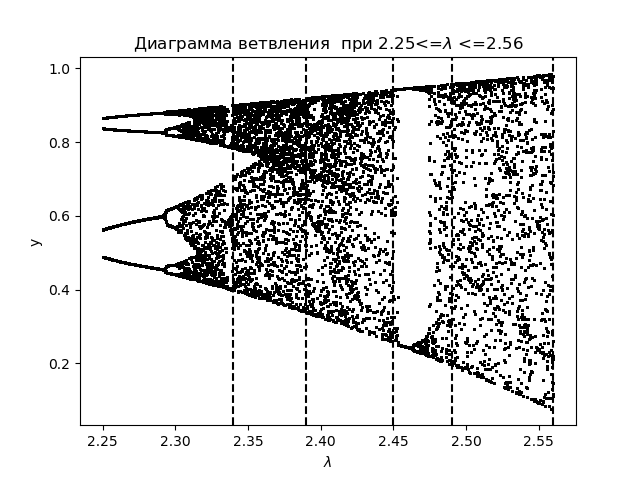
Построим график для энтропийного коэффициента при тех же областях $inline$ :

График энтропийного коэффициента

import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(2.25,2.56,0.0001):     q=[round(p,2)]         M=zeros([1001,1])         for j in arange(0,1,1):         M[0,j]=0.5     for j in arange(0,1,1):         for i in arange(1,1001,1):             M[i,j]=q[j]*M[i-1,j]*(1-(M[i-1,j])**2)                a=[]        for i in arange(0,1001,1):         a.append(M[i,0])     n=len(a)     z=histogram(a, bins=m)     if type(m) is str:         m=len(z[0])         y=z[0]             d=z[1][1]-z[1][0]     h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)     ke=round(h/std(a),3)     data_k.append(ke) plt.figure(2) plt.title("Энтропийный коэффициент ke для 2.25<= $lambda$ <=2.56") plt.plot(arange(2.25,2.56,0.0001),data_k) plt.xlabel("$lambda$ ") plt.ylabel("ke") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.grid() plt.show()

Получим: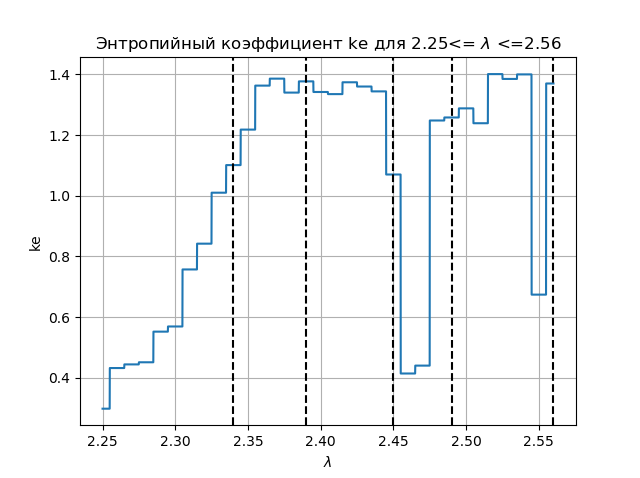

Сравнивая диаграмму и график, видим идентичное отображение областей на диаграмме и на графике для энтропийного коэффициента для функции $x_{n+1}=f(x_{n})=lambda cdot x_{n}cdot (1-x_{n}^{2})$ .