
Совсем недавно команда исследователей из компании DeepMind, которая специализируется на разработке различных ИИ-алгоритмов, опубликовала интересную научную статью. Она называется «Advancing mathematics by guiding human intuition with AI» и опубликована в авторитетном научном журнале Nature. В ней затрагивается вопрос интуиции человека и машинного обучения.
Многие специалисты уже обратили внимание на статью, причем часть из них считают работу DeepMind прорывом, а часть — обычным исследованием, значение которого преувеличивается журналистами. Но как бы там ни было, а сама работа весьма интересна, поскольку ее результаты дают возможность расширить инструментарий математиков. Речь идет о демонстрации сложных корреляций в одной из гипотез теории узлов из абстрактной математики. Кроме того, алгоритм от DeepMind нашел применение в изучении комбинаций белковых последовательностей. Необычным во всем этом является то, что для решения указанных задач ИИ от DeepMind показал признаки «сильного ИИ».
Что здесь необычного?

Дело в том, что в ходе работы алгоритм нашел доказательство одной из теорем. Для этого необходима комбинация различных навыков, а также построение логической цепочки из множества звеньев. Ранее считалось, что на такое способен лишь человек, но, похоже, ИИ начинает понемногу осваивать сферы, которые считались недоступными для машин. Не будем уже вспоминать игру го, в которой ИИ от DeepMind победил несколько лет назад. Сейчас никто из людей неспособен выиграть у машины, несмотря на то, что совсем недавно го считалась тоже недоступной для машин. Но постепенно се меняется.
Компании DeepMind удалось создать модель, которая научилась работать с доказательством теорем, так что, скорее всего, подобные модели станут использовать математики. Исследователи из DeepMind показали, что ИИ-алгоритмы могут использоваться учеными для поиска новых путей разработки теорем.
В текущем случае модель создала гипотезу из области топологии и теории представлений. Речь идет о теории узлов, которая дает возможность изучить узлы веревки, два конца которой соединены вместе. Кроме того, она же помогла вывести доказательство теоремы о структуре узлов. Причем ей это удалось сделать без дополнительных вводных данных, которые подтверждают правильность теоремы. Выявленные корреляции были достаточно необычными — математики не сразу смогли понять часть данных, оценив лишь после детального изучения работы машины.
В чем сложность?
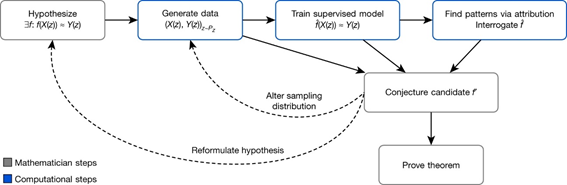
В ходе анализа результатов работы модели специалисты пропустили часть закономерностей, предоставленных ИИ. Сначала на них просто не обратили внимание. Лишь потом, в ходе детального анализа, оказалось, что эти данные крайне важны, просто закономерности, полученные ИИ, настолько сложные, что люди не смогли сразу понять, что это и как связано с доказательством.
Часть проблемы в том, что ИИ вывел новые закономерности и корреляции — математики ожидали привычных для себя доказательств. Но оказалось, что часть предложенных ИИ данных содержит новые открытия. По словам одного из авторов исследования, четвертая и пятая переменные от ИИ соответствовали концепции, но их сразу не приняли во внимание. «ИИ все время понимал, что происходит», — заявил Марк Лакенби из Оксфордского университета. Он добавил, что после того, как эти данные были учтены, команде удалось закончить гипотезу, доказав теорему. Некоторые выявленные корреляции были крайне неинтуитивными, так что человеку было сложно понять, что перед ним.
ИИ от DeepMind использовал предоставленные компоненты теории, алгебраический и геометрический, и смог найти корреляции, как прямые, так и побочные, косвенные. Представители проекта не ожидали настолько четкой связи между алгебраическими и геометрическими величинами, поэтому не сразу осознали и глубину проработки задачи машиной. Оказалось, что сигнатура, алгебраическая величина, была напрямую связана с геометрией узла. Используя методы атрибуции из машинного обучения, удалось открыть новую величину, названную естественным уклоном.

Сама задача решалась не для того, чтобы изучить сами узлы. Дело в том, что результаты работы найдут применение в квантовой теории поля и неевклидовой геометрии. Новая гипотеза о том, что алгебраический и геометрический инварианты теории узлов связаны, открывает новые перспективы в изучении математики узлов.
Что за нейросеть использовалась и какие данные у нее были?
Используя программный пакет SnapPy, исследователи сгенерировали «сигнатуру», алгебраический инвариант и 12 многообещающих гиперболических инвариантов для 1,7 миллиона узлов с количеством пересечений вплоть до 16.

Затем они создали полностью связанную нейронную сеть с прямой связью с тремя скрытыми слоями по 300 единиц в каждом. Они обучили модель глубокого обучения отображать значения гиперболических инвариантов в сигнатуре. Их первоначальная модель могла предсказать сигнатуру с точностью 78 процентов. Дальнейший анализ привел их к меньшему набору параметров в гиперболических инвариантах, которые предсказывали сигнатуру. Исследователи уточнили свою гипотезу, сгенерировали новые данные, переобучили свои модели и пришли к окончательной теореме.
Здоровый скептицизм

О значении работы мы уже рассказали выше. Некоторые ученые считают его весьма значительным, другие, как, например, математик Эрнест Дейвис из Университета Нью-Йорка, утверждают, что значение работы несколько преувеличено. Так, он отмечает, что теория узлов — это не та проблема, в которой глубокое обучение обычно значительно превосходит другие технологии, включая иные методы машинного обучения или статистические методы.
В задаче о узле было всего двенадцать входных характеристик, из которых только три оказались актуальными. А математическая связь между входными характеристиками и целевой переменной была простой.
Вторая претензия Дейвиса состоит в том, что в статье ученых встречается слово «интуиция» в применении к ИИ-алгоритму. На самом деле авторы проекта подразумевают просто способность ИИ проанализировать множество данных и выявить корреляции. Обычно под «интуицией» подразумевается возможность человека сделать важные выводы на основе предыдущего опыта без явных вычислений или пошаговых рассуждений. В случае ИИ это понятие не применимо, антропоморфизм в технологиях лишь мешает пониманию принципов работы таких систем.
В любом случае, эта работа имеет важное значение как для математики, так и для направления ИИ-технологий. Сейчас машинное обучение и нейросети помогают во многих отраслях науки и техники. Математика — не исключение.


