Сегодня я расскажу Вам очень показательную историю про одну математическую гипотезу из теории чисел. Она станет ярким примером того, как в математике прерываются, казалось бы, явные закономерности, и что любое предположение в этой науке нуждается в строгом доказательстве, даже если оно проверено для всех чисел, которые только могут поместиться в память суперкомпьютера.

Итак, в 1919 году венгерский математик Дьёрдь Пойя, изучая вопросы, связанные с факторизацией (разложением на простые множители) чисел, выдвинул далеко идущую гипотезу. Суть её такова.
Числа, большие единицы, можно разделить на два класса:
-
Имеющие нечетное количество множителей в разложении.
-
Имеющие четное количество множителей в разложении.
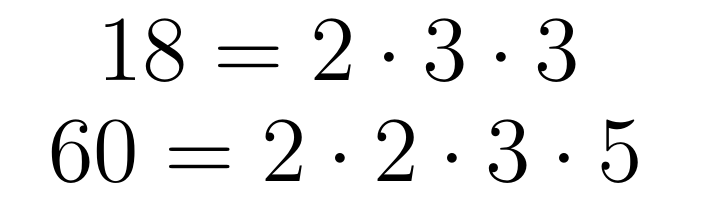
Гипотеза Пойи утверждала, что чисел первого класса не меньше, как далеко бы мы не уходили на бесконечность. Действительно, Пойя проверил данное утверждение и, казалось, тенденция была видна невооруженным глазом.
Впрочем, жизнь любой гипотезы в математике непредсказуема, ведь иногда достаточно всего одного контрпримера, чтобы разрушить её фундамент.
Функция Лиувилля
Гипотеза в том виде, что я показал выше, естественно, требует представления в виде формул и условий, но волноваться из-за этого не стоит.
В теории чисел на каждый особый случай есть своя уникальная функция, да еще и именная.

Функция Луивилля, в общем-то, делает именно то, что нужно для формализации гипотезы Пойи:
-
принимает значение «1», если у числа чётное количество простых множителей в разложении;
-
принимает значение «-1» в противном случае.
С использованием функции Лиувилля гипотеза переформулируется следующим образом:
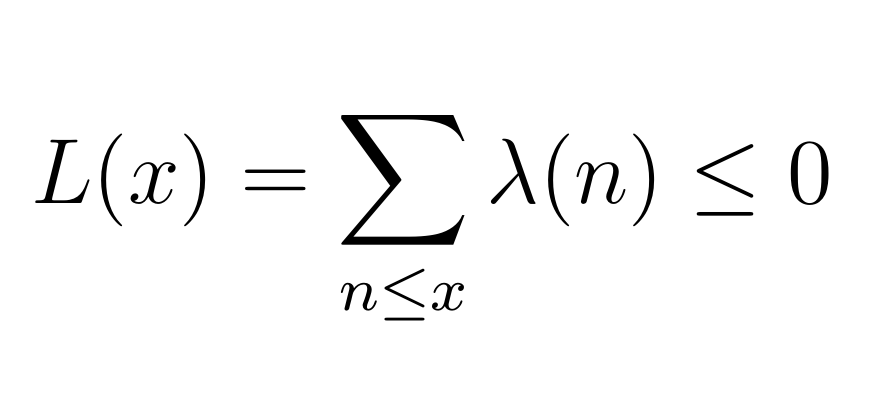
Простейший код для вычисления на Python:
def prime_factors_with_counts(n):
factors = {} # Словарь для хранения простых множителей и их количества
i = 2
while i * i <= n:
if n % i:
i += 1
else:
n //= i
factors[i] = factors.get(i, 0) + 1
if n > 1:
factors[n] = factors.get(n, 0) + 1
return factors
def liouville(n):
factors_with_counts = prime_factors_with_counts(n)
total_factors = sum(factors_with_counts.values())
return 1 if total_factors % 2 == 0 else -1
def cumulative_liouville(n):
cumulative_values = []
cumulative_value = 0
for num in range(1, n + 1):
liouville_result = liouville(num)
cumulative_value += liouville_result
cumulative_values.append(cumulative_value)
return cumulative_values
# Ввод числа N
N = int(input("Введите натуральное число N: "))
if N < 1:
print("Введите число больше или равное 1.")
else:
output_filename = "liouville_table.txt"
with open(output_filename, "w") as file:
file.write("Число | Разложение на простые множители | Функция Луивилля | Кумулятивная Луивилля\n")
file.write("-" * 68 + "\n")
cumulative_values = cumulative_liouville(N)
for num in range(1, N + 1):
factors = prime_factors_with_counts(num)
liouville_result = liouville(num)
cumulative_result = cumulative_values[num - 1]
factors_str = " * ".join([f"{factor}**{count}" if count > 1 else str(factor) for factor, count in factors.items()])
file.write(f"{num:^6} | {factors_str:^36} | {liouville_result:^15} | {cumulative_result:^21}\n")
print(f"Таблица сохранена в файле '{output_filename}'.")Приведенный выше код считает значение функции Лиувилля для каждого числа, вычисляет кумулятивную функцию, а затем выводит результаты в файл. Ниже пример графика для N=250 000 (автор гипотезы вручную проверил все значения до N=1500, а в 1940 году некий индиец «досчитал» до 20 000):
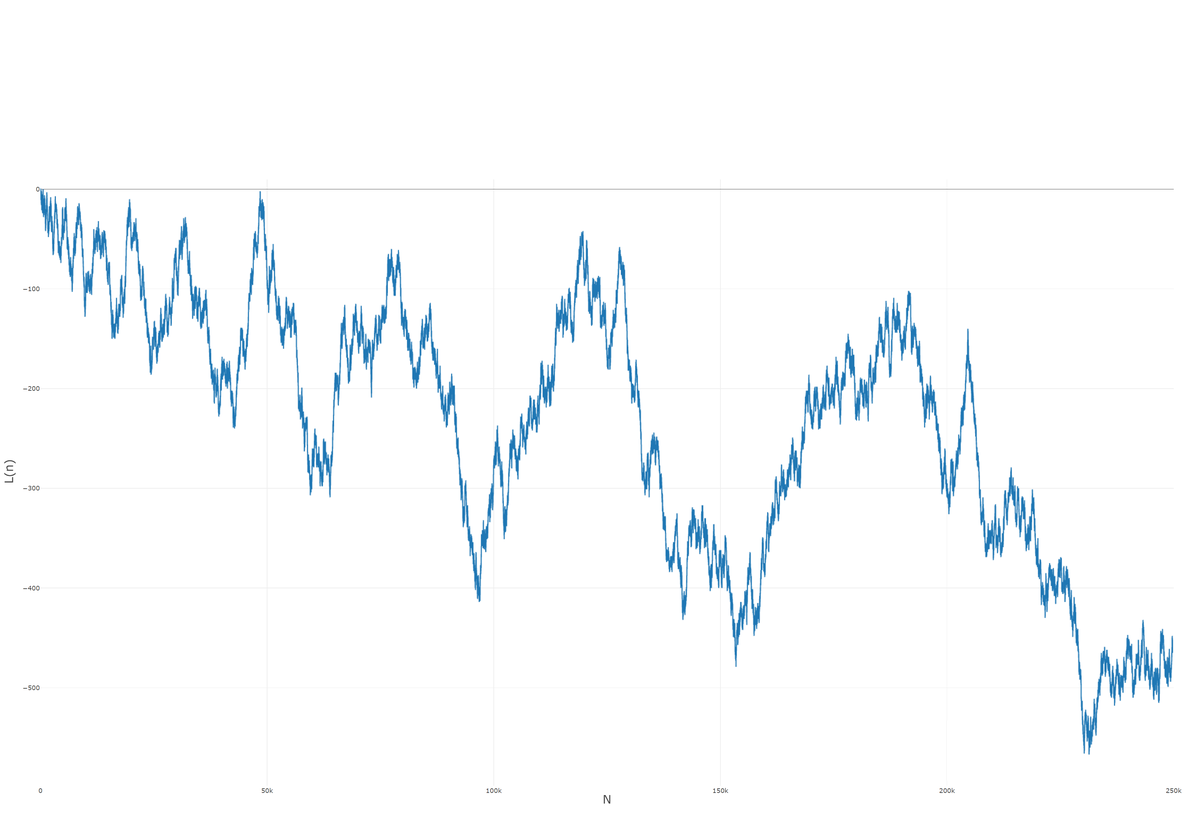
Как мы видим по графику, значения лежат в отрицательной области, да и тренд как бы намекает на ясный статус гипотезы…

В защиту Пойа: гипотезу он взял не просто из головы, а затем проверил на конкретных примерах. Математик изучал квадратичные формы, исследовал решения уравнения L(x) = 0, показал, что в большинстве случаев функция будет отрицательной и перехода через ось абсцисс не будет. Проблема была в том, что он рассмотрел не все возможные варианты.
Кроме того, некоторые источники отмечают, что математик никогда и не предполагал, что это утверждение истинно; скорее, он показал, что истинность утверждения подразумевает гипотезу Римана.
…прошло 40 лет
В 1958 году английский математик Колин Брайан Хазелгроув находит не конструктивный пример, опровергающий гипотезу Пойи. В своей статье он проворачивает довольно интересный приём, используя связь функции Лиувилля с дзета-функцией Римана:
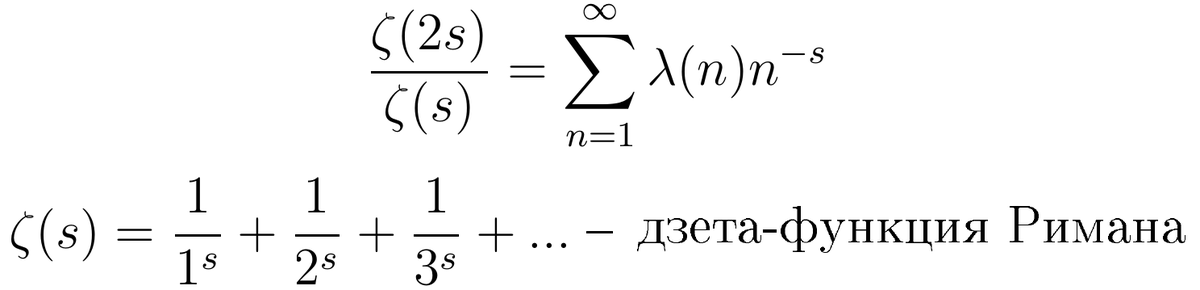
Автор использует введенные еще до него функции (их пытались использовать для доказательства гипотезы Римана), оценив которые, можно сделать вывод о поведении кумулятивной функции Лиувилля:
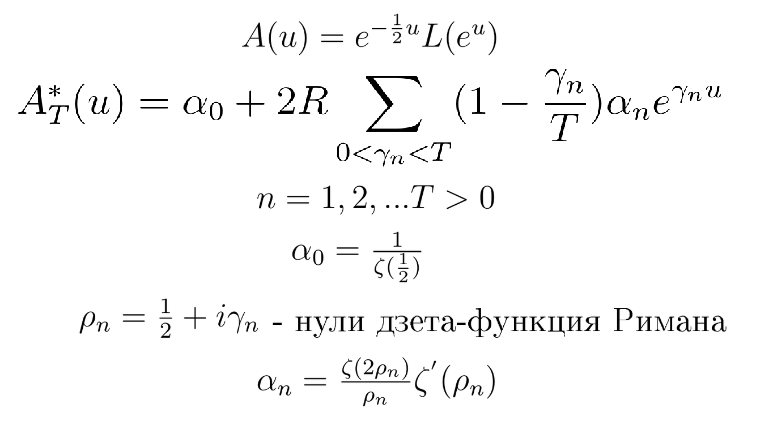
Те же предшественники Хазелгроува показали, что:
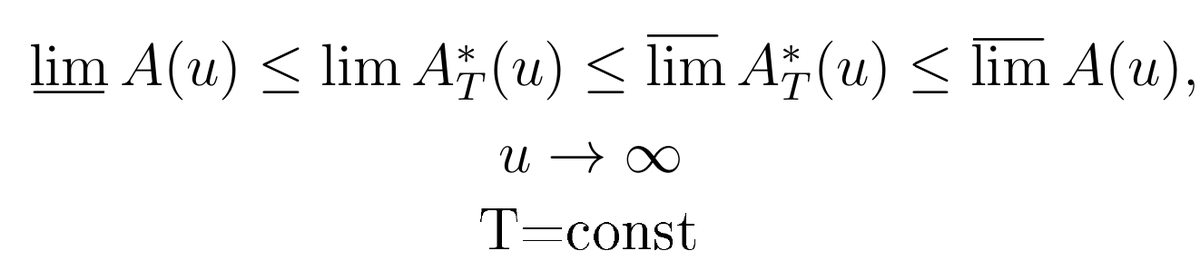
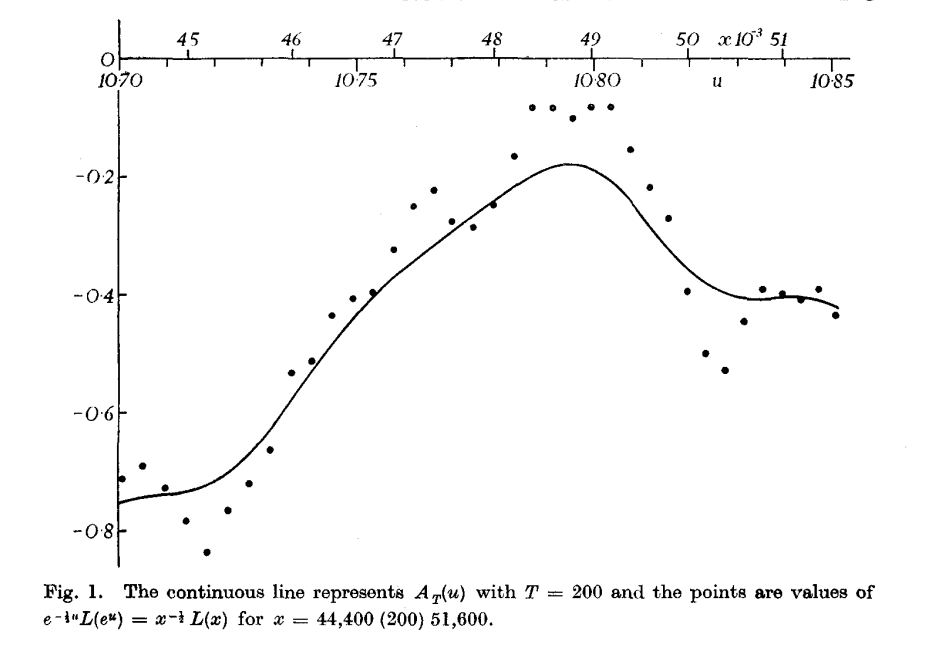
и, что самое главное, что функция А*(T,u) — периодическая! Т.е. у неё есть некоторый диапазон значений:
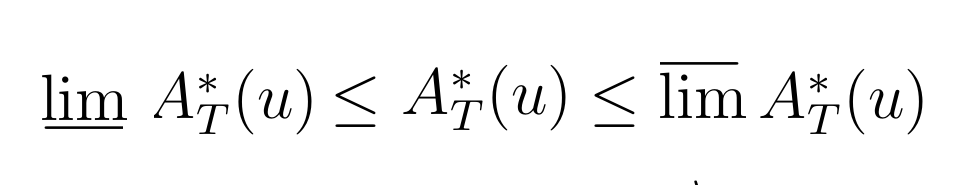
Схематичная иллюстрация выражения выше:

Поэтому, если получится найти Т и u, при которых А*(T,u) > 0, из этого будет следовать
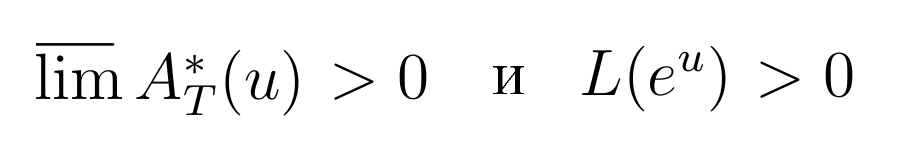
, что приведет к опровержению гипотезы Пойи!
Естественно, Хазелгроув нашёл такие числа. Однако вспомните, что я в начале статьи говорил про неконструктивное доказательство. Англичанин привел не конкретное число, на котором гипотеза «ломается», а некоторый диапазон, где по его расчетам кумулятивная функция Лиувилля поменяет свой знак.
В оригинальной статье приводится Хазелгроув пишет, что они заметили, что наибольший вклад в функцию А*(T,u) вносят первый, второй и седьмой нули дзета-функции Римана. Таким образом при T=1000 удалось «выцепить» набор возможно подходящих значений u:
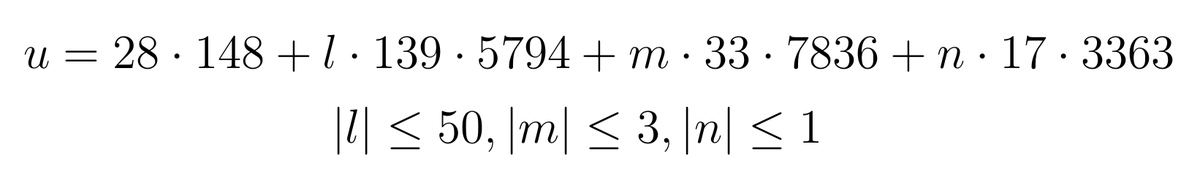
Круг сузился, а расчёты на имевшихся в распоряжении математиков компьютерах EDSAC I и Mark I стали выполнимы за разумное время.

В итоге получили, что переход исследуемой функции, а значит и кумулятивной функции Лиувилля через ось абсцисс должен произойти при 831 < u < 847, что соответствует:
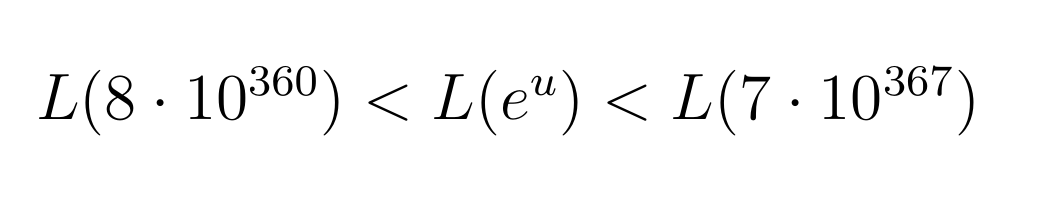
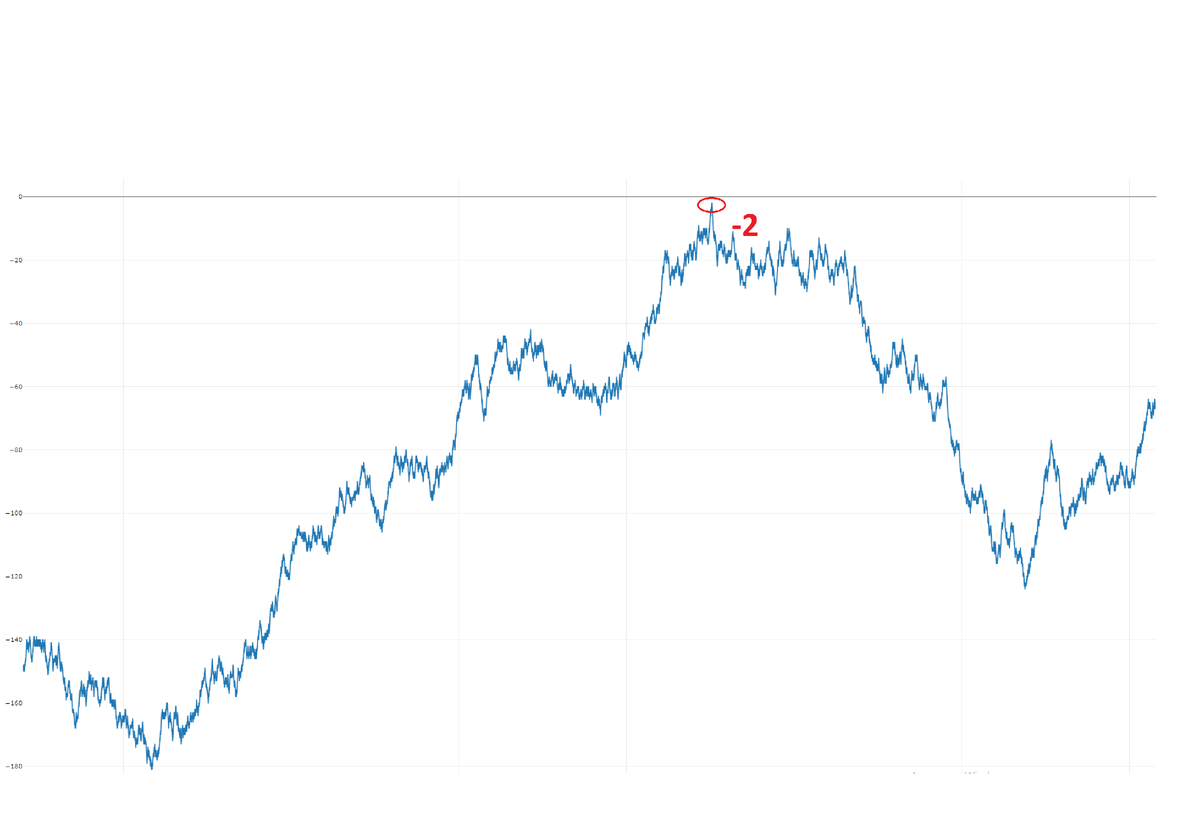
Первый конкретный пример числа, на котором ломается гипотеза Пойи появился в 1960 году. Им стало число 906 180 359, а через 20 лет был найден наименьший на сегодняшний день показатель — 906 150 257. Интересно, что в этом диапазоне функция достигает своего максимального значения в 849:
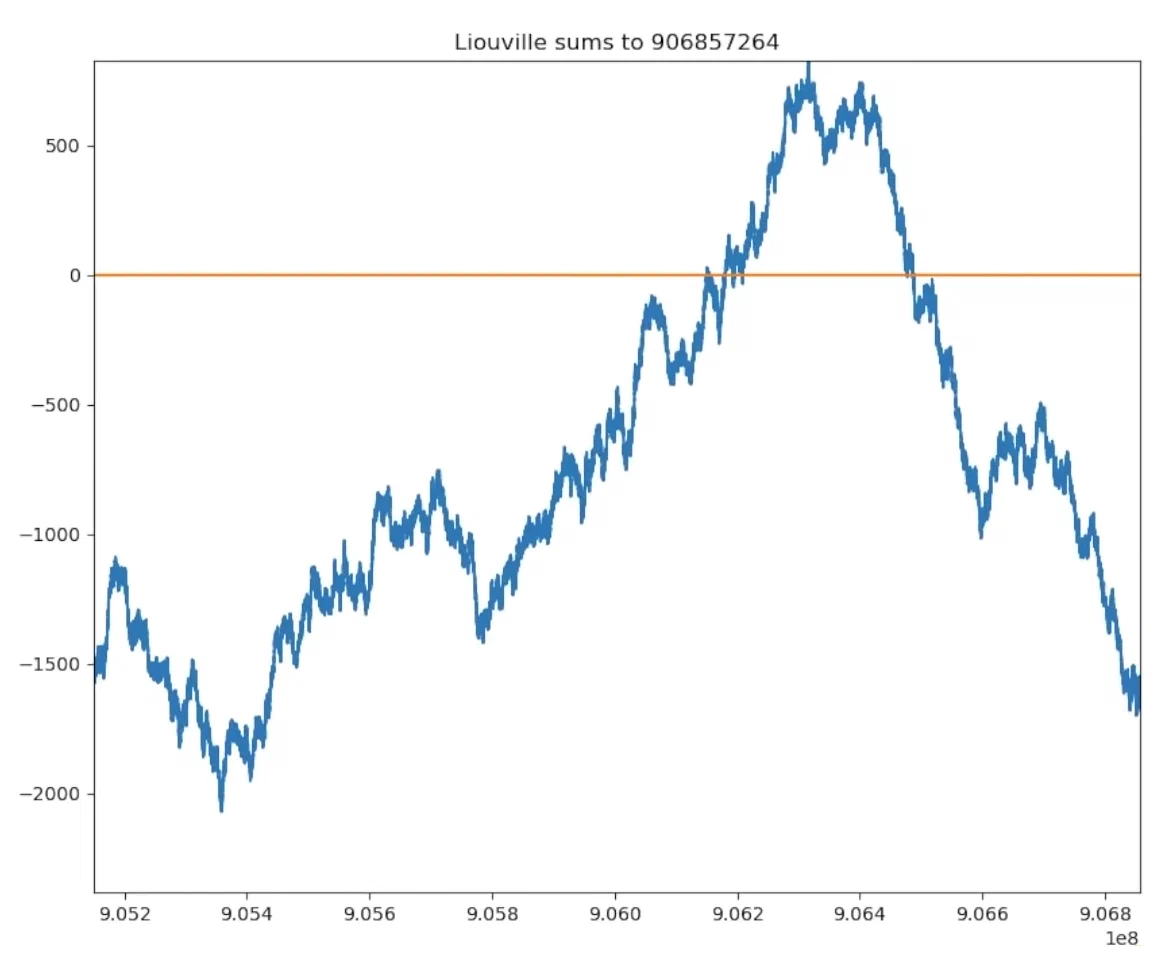
А вот так ведут себя минимумы кумулятивной функции.
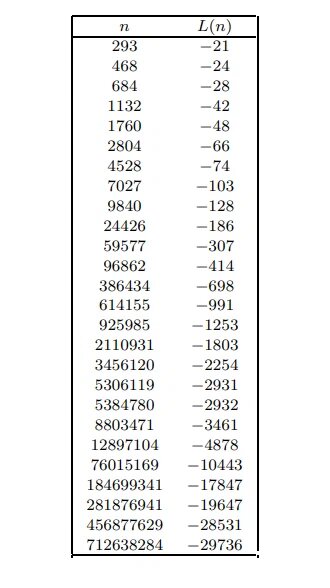
Как Вы понимаете, любители экстраполяции здесь бы не получили результата!

На данный момент гипотеза Пойи еще представляет научный интерес. Во-первых, не ясно, бесконечное ли количество раз кумулятивная функция меняет знак. Во-вторых, у опровергнутой гипотезы еще сохранились «мостики» с гипотезой Римана, истинность которой, к слову, проверена для первых 10 триллионов нетривиальных нулей. Но мы же теперь, не верим на слово.
-
В Телеграмм » Математика не для всех» доступен архив с оригиналами статей по гипотезе Пойи.


