Сегодня у нас достаточно простая статья, связанная с занимательной математикой. Я думаю, все прекрасно, знают, что такое факториал:
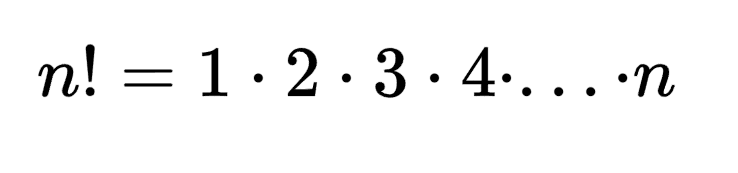
Более изощренные любители математики знают и про такое понятие, как субфакториал:

Субфакториал
Субфакториал (или subfactorial) — обозначается символом !n и представляет собой количество перестановок n элементов, в которых ни один элемент не остается на своем месте (по сути — это аналогия полного беспорядка). Для небольших значений n это можно проиллюстрировать следующим образом:
-
Для n = 1: !1 = 0. Единственный элемент не может «переставляться» сам с собой.
-
Для n = 2: !2 = 1. Всего две возможные перестановки (1, 2) и (2, 1), и только одна из них соответствует требованию «ни один не остается на своем месте».
-
Для n = 3: !3 = 2. Возможные перестановки: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). В двух из них ни один элемент не остается на своем месте: (2, 3, 1) и (3, 1, 2).

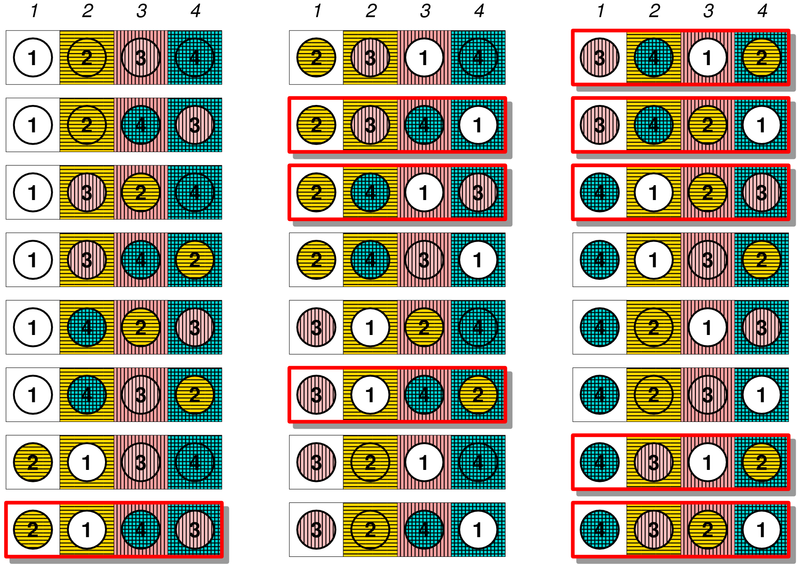
Более жизненная интерпретация субфакториала: профессор дал тест 4 студентам – 1, 2, 3 и 4 – и хочет, чтобы они оценили тесты друг друга. Конечно, ни один студент не должен оценивать свой собственный тест. Сколько существует способов, чтобы никто не получил обратно свой собственный тест для проверки?.
Первые десять значений субфакториалов натуральных чисел:
-
!1 = 0
-
!2 = 1
-
!3 = 2
-
!4 = 9
-
!5 = 44
-
!6 = 265
-
!7 = 1854
-
!8 = 14833
-
!9 = 133496
-
!10 = 1334961
Если внимательно присмотреться к формуле субфакториала, то можно увидеть, что она очень похожа на формулу разложения экспоненты в ряд Тейлора:

Если подставить «-1» вместо n, то можно получить любопытное отношение между факториалом и субфакториалом:

Эта величина — предел вероятности того, что выбранная во множестве перестановка является полным беспорядком. А еще можно увидеть, что !n является ближайшим целым числом к n!/e:

Субфакторион
Теперь перейдем к субфакторионам — числам, которые равны сумме субфакториалов своих цифр. Для начала определим верхнюю границу таких чисел. Итак:.
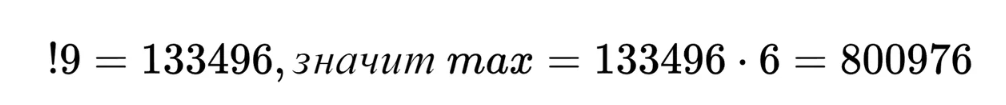
Теперь нам нужен простейший код на Python и онлайн-компилятор:.

Итоговый результат, который выдала программа :

И это единственное число, которое носит гордое название «субфакторион». Первые его следы можно найти в достаточно интересной книжке 1966 года «Математика на каникулах»:.

На странице 167 есть упоминание этого факта:.

Покопавшись еще в сети, удалось найти превью статьи из «Mathematical Magazine» с упоминанием факта, что субфакторион впервые был найден в 1966 году с применением ЭВМ:.

Однако, стоит заметить, что мой «топорный» код выполнялся бы на компьютерах середины 70-х очень долго. Так что стоит отдать почести простым студентам-энтузиастам за программирование решения такой интересной задачки.
-
Больше математики в Telegram — «Математика не для всех«.


