
День числа Пи — это ежегодный праздник, посвящённый математической константе π (отношению длины окружности идеального круга к его диаметру). День числа Пи отмечается 14 марта (3-й месяц), поскольку 3, 1 и 4 — первые три значащие цифры числа π. Он был основан в 1988 году Ларри Шоу, сотрудником научного музея «Эксплораториум» в Сан-Франциско (Калифорния). Празднования часто сопровождаются поеданием пирога или проведением соревнований по цитированию цифр числа Пи наизусть. В 2009 году Палата представителей Конгресса США поддержала предложение о праздновании Дня числа Пи. 40-я Генеральная конференция ЮНЕСКО объявила День числа Пи Международным днём математики в ноябре 2019 года. Альтернативные даты праздника — 22 июля (22/7, приближение к π) и 28 июня (6,28, приближение к 2π или тау).
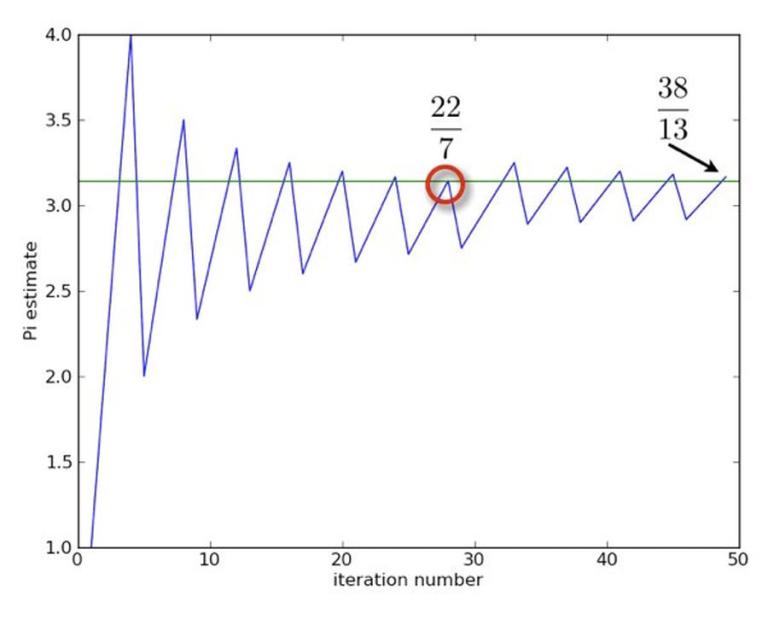
1) π нельзя вычислить точно, потому что его невозможно представить в виде дроби
Если вы можете представить число в виде дроби (отношения) двух целых чисел, то есть двух целых чисел с положительным или отрицательным значением, то это число, значение которого вы можете узнать точно. Это верно для чисел, дроби которых записываются без периода, например 2/5 (или 0,4), и верно для чисел, дроби которых записываются с периодом, например 2/3 (или 0,666666…).
Но π, как и все иррациональные числа, нельзя представить таким образом — и, следовательно, его не получится вычислить точно. Все, что мы можем сделать — это вычислить π приблизительно. И хотя мы делаем это очень хорошо с помощью наших современных математических методов и вычислительных инструментов, мы неплохо с этим справлялись уже пару тысячелетий назад.

2) Метод Архимеда используется для приближённого определения π уже более 2000 лет
Вычислить площадь круга сложно — особенно если вы ещё не знаете, что такое “π”. Но вычислить площадь правильного многоугольника легко, особенно если вы знаете формулу площади треугольника и понимаете, что любой правильный многоугольник можно разбить на набор из равнобедренных треугольников. У вас есть два пути:
- вы можете вписать правильный многоугольник внутрь круга и учитывать, что «истинная» площадь круга должна быть больше его,
- или вы можете построить правильный многоугольник снаружи круга и учитывать, что «истинная» площадь круга должна быть меньше этой площади.
Чем больше сторон у правильного многоугольника, тем ближе к значению π. В III веке до н.э. Архимед взял эквивалент 96-гранного многоугольника для приближённого определения π и обнаружил, что оно должно лежать между двумя дробями 220/70 (или 22/7, поэтому в Европе день π отмечается 22 июля) и 223/71. Десятичные эквиваленты этих двух приближений — 3,142857… и 3,140845…, что весьма впечатляет для двух с лишним тысяч лет назад!

3) Приближение для π, известное как «Милю», открытое китайским математиком Цзу Чунчжи, было лучшим дробным приближением π в течение примерно 900 лет
В V веке математик Цзу Чунчжи открыл замечательное дробное приближение π: 355/113. Для тех из вас, кому нравится десятичное приближение π, оно получается равным 3,14159292035… что соответствует первым семи цифрам π и отличается от истинного значения всего на 0,0000002667, или на 0,00000849%. Это самое долгоиграющее лучшее приближение в письменной истории.
На самом деле, если вы будете пытаться вычислить дробные приближения π, постоянно увеличивая знаменатель, то вы не найдёте лучшего варианта, чем 355/113, пока не наткнётесь на дробь 52163/16604, которая, впрочем, лишь немногим лучше. Если 355/113 отличается от истинного значения π на 0,00000849%, то 52163/16604 отличается от истинного значения π на 0,00000847%.
Эта замечательная дробь, 355/113, была лучшим приближением к π, существовавшим до конца 14-го — начала 15-го века. Именно тогда индийский математик Мадхава из Сангамаграмы придумал более совершённый метод приближения π: метод, основанный на суммировании бесконечных рядов.
4) π не просто иррациональное число – оно ещё и трансцендентное
Чтобы число было рациональным, оно должно записываться в виде дроби с целыми числами в числителе и знаменателе. По этому признаку π является иррациональным — как и, например, квадратный корень из целого положительного числа, типа √3. Однако существует большое различие между числом типа √3, которое известно как «действительное алгебраическое» число, и π, которое является не только иррациональным, но и трансцендентным.
Если вы можете записать полиномиальное уравнение с целочисленными экспонентами и коэффициентами и использовать только суммы, разности, умножение, деление и экспоненты, то все реальные решения этого уравнения будут реальными алгебраическими числами. Например, √3 является решением полиномиального уравнения x² — 3 = 0, а другим его решением является -√3. Но ни для одного трансцендентного числа, включая π, e и γ, таких уравнений не существует.
На самом деле, одна из самых известных в истории нерешённых математических головоломок заключается в том, чтобы построить квадрат с такой же площадью, как у круга, используя только циркуль и линейку. И невозможность её решить была строго доказана только в 1882 году, что демонстрирует, насколько сложно в математике бывает доказать то, что кажется очевидным.
5) Вы можете очень просто построить приближение к π, бросая дротики
Хотите получить приблизительное значение π, но не хотите заниматься сложной математикой? Нет проблем, просто возьмите круг, нарисуйте вокруг него квадрат, одна сторона которого точно равна диаметру круга, и начните бросать дротики. Вы сразу же обнаружите, что:
- некоторые дротики попадают внутрь круга (вариант 1),
- некоторые дротики попадают за пределы круга, но внутрь квадрата (вариант 2),
- и некоторые дротики попадают за пределы квадрата и круга (вариант 3).
Если ваши дротики будут попадать в истинно случайные места, вы обнаружите, что отношение «дротиков, попавших внутрь круга (вариант 1)» к «дротикам, попавшим внутрь квадрата (варианты 1 и 2 вместе)» равно π/4. Этот метод аппроксимации π является примером техники моделирования, очень часто используемой в физике частиц: метод Монте-Карло. Если вы напишете компьютерную программу для моделирования этой игры в дартс, то вас можно будет поздравить: вы только что написали свою первую симуляцию Монте-Карло!
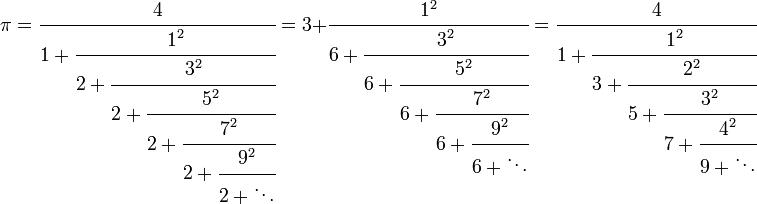
6) Вы можете довольно неплохо и относительно быстро построить приближение к числу π с помощью непрерывной дроби
Хотя вы не можете представить π в виде простой дроби, вы можете представить его в виде непрерывной дроби. У такой дроби в знаменатели стоят дроби, у которых в знаменателе стоят ещё дроби, и так далее. Чем больше дробей вы вычисляете, тем более точное приближение у вас получается.
Существует множество примеров формул, которые можно использовать для приближения к числу π через повторения, но преимущество трёх приведённых на картинке выше формул в том, что они просты, понятны и дают отличное приближение при относительно небольшом количестве членов. Например, использование только первых 10 членов последней показанной серии дробей правильно даёт первые 8 цифр π, с небольшой ошибкой в 9-й цифре. Большее количество членов даёт лучшее приближение.

7) После 762 цифр π встречается шесть девяток подряд
Это математическое совпадение стало знаменитым благодаря идее о том, что можно запомнить цифры числа π до этого момента, а потом пошутить насчёт рациональности π. Самое раннее известное упоминание этой идеи встречается в книге Дугласа Хофштадтера «Метамагические темы» 1985 года, где Хофштадтер пишет:
Я сам однажды выучил 380 цифр числа π, когда был сумасшедшим школьником. Моей недостижимой мечтой было дойти до того места в 762 знака в десятичной системе счисления, где будет «999999», чтобы я мог произнести его вслух, дойти до этих шести девяток, а затем в шутку заявить: «И так далее!».
Эту последовательность из шести девяток иногда называют «точкой Фейнмана», в честь физика Ричарда Фейнмана, который якобы высказал эту идею в одной из лекций. Однако неясно, когда и сделал ли Фейнман такое заявление; оно не упоминается ни в опубликованных биографиях, ни в автобиографиях, и неизвестно его биографу Джеймсу Глику.
Теперь мы вступаем на территорию, требующую довольно сложных вычислений. Многие люди задавались вопросом: «Какие закономерности можно найти в числе π?». Если выписать первые 1 000 цифр, то уже и в них можно обнаружить несколько интересных закономерностей:
- 33-я цифра числа π – это ноль. Именно так далеко нужно зайти, чтобы найти в записи числа π все 10 цифр, от 0 до 9.
- В первых 1000 цифрах π есть несколько случаев «трижды повторяющихся» чисел подряд, включая «000» (два раза), «111» (два раза), «555» (два раза) и «999» (два раза).
- При этом эти две тройки из девяток находятся рядом друг с другом; после 762-й цифры числа π вы увидите шесть девяток подряд.
Можно доказать, что где-то в π встречаются любые комбинации и последовательности цифр; но при этом вы не найдёте строку из 7 одинаковых цифр подряд, пока не выпишите почти 2 миллиона цифр π!
8) Вы можете вычислить π с точностью до 31 цифры, разделив два обычных на вид иррациональных числа
Одно из самых причудливых свойств π заключается в том, что оно появляется в очень неожиданных местах. Хотя формула eiπ = -1 является, пожалуй, самой известной — но, возможно, лучший и ещё более странный факт заключается в следующем: если взять натуральный логарифм 18-значного целого числа 262 537 412 640 768 744, а затем разделить его на квадратный корень числа 163, то получится число, идентичное π вплоть до 31-й цифры.
Почему это так, и как мы дошли до такого хорошего приближения для π?
Оказывается, в 1859 году математик Шарль Эрмит обнаружил, что комбинация трёх иррациональных (и двух трансцендентных) чисел e, π и √163 даёт так называемое «почти целое число»: e π√163 почти точно оказывается целым. Это будет число, почти равное 262 537 412 640 768 744 – а именно, 262 537 412 640 768 743,99999999999925…
9) У нескольких знаменитых в области физики, астрономии и космонавтики людей день рождения приходится на день π
Первый из них – сам Альберт Эйнштейн, родившийся 14 марта 1879 года. Известный своим вкладом в теорию относительности, квантовую механику, статистическую механику и эквивалентность энергии и массы, Эйнштейн также самый известный человек из родившихся в день π.
Следующий — Фрэнк Борман, родившийся 14 марта 1928 года, которому в этот день в 2023 году исполнилось 95 лет. Он командовал «Джемини-7» и был связным НАСА в Белом доме во время высадки на Луну «Аполлона-11», но наиболее известен как командир корабля «Аполлон-8», который стал первой экспедицией, доставившей астронавтов на Луну, облетевшей вокруг Луны и сфотографировавшей место «восхода» Земли над горизонтом Луны.
Третий, возможно, наименее известный сегодня человек — это Джованни Скиапарелли, родившийся 14 марта 1835 года. Благодаря его работам XIX века, мы получили самые подробные на то время карты скалистых планет нашей Солнечной системы (кроме нашей): Меркурия, Венеры и Марса.
Ещё один человек — Джин Сернан, родившийся 14 марта 1934 года, который (на данный момент) является последним человеком, ступившим на Луну. Он вошёл в лунный модуль «Аполлона-17» вслед за другим членом экипажа Харрисоном Шмиттом. Сернан умер 16 января 2017 года в возрасте 82 лет.

10) Существует знаменитое звёздное скопление, внешне похожее на букву “π”
На фото выше представлено открытое звёздное скопление Мессье-38, которое можно найти, сначала обнаружив яркую звезду Капеллу, третью по яркости звезду в северном полушарии (после Арктура и Ригеля), а затем переместившись примерно на треть пути по направлению к Бетельгейзе. Прямо в этом месте, не доходя до звезды Альнат, вы найдёте звёздное скопление Мессье-38. На композитном фото из красного, зеленого и синего цветов отчётливо видна знакомая нам форма.
В отличие от самых новых и молодых звёздных скоплений, ни одна из оставшихся в Мессье-38 звёзд никогда не станет сверхновой: масса всех выживших звёзд слишком мала для этого. Самые массивные звезды в скоплении уже умерли, и теперь, спустя примерно 220 миллионов лет после их образования, остались только звезды классов A, F, G (похожие на Солнце) и более холодные. И что примечательно, самые яркие и голубые из выживших звёзд образуют на небе приблизительную π-форму. Существует ещё четыре относительно близких к нам звёздных скопления, но ни одно из них не связано Мессье-38, которое расположено на расстоянии 4200 световых лет от нас и содержит сотни, а возможно, даже тысячи звёзд. Так что благодаря этому скоплению вы можете увидеть π в небе.


