
Формулы и “багаж”
Что это такое? Вряд ли эта формула что-то говорит вам. А если я напишу ее так:
То вы сразу узнаете в ней закон Ньютона. Конечно, обе формулы эквивалентны, мы просто привыкли, что сила обозначается F, масса m, более того, мы подразумеваем, что дело происходит в трехмерном пространстве, что у тел есть координаты, итд. То есть у теории есть две составляющие: формулы и бла-бла вокруг них. Макс называет вторую компоненту словесным багажом.
Рассмотрим дерево существующих теорий:
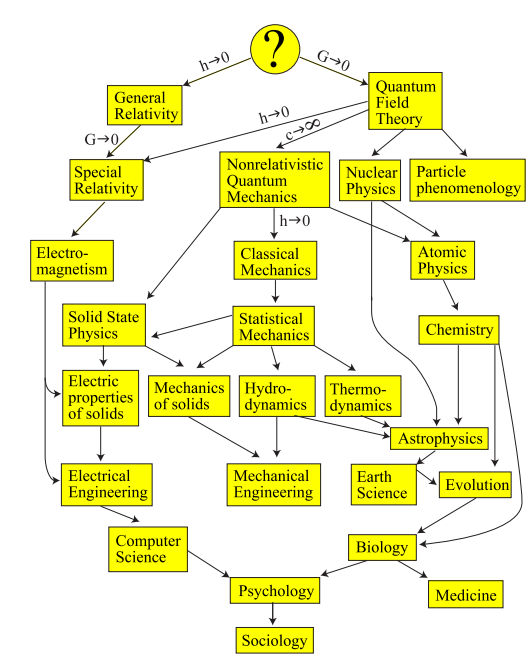
В самом низу находится социология, где почти нет формул, но много слов. Постепенно двигаясь наверх, мы встречаемся со все более усложняющейся математикой. А вот со словами все хуже и хуже: попробуйте у ученого, который занимается фундаментальной физикой, выведать, что такое время. Это вам очевидно, что время это последовательность событий и оно течет вперед. Чем больше вы знаете и чем глубже погружаетесь, тем менее это становится очевидным. Описание того, что такое время, все больше схлопывается к тому, что время – это буквочка t, которая участвует в таких-то уравнениях.
Итак, Макс замечает, что:
По мере движения к все более фундаментальному уровню математика становится все более сложной, а багаж начинает все больше вырождаться. В пределе, предполагает Макс, у ТОЕ (Theory of Everything – Общей Теории Всего) нет багажа. Итак, TOE состоит только из формул.
Это первый ингредиент. Запомним его.
Физика “Наоборот”
Как такое вообще возможно? Физика пытается найти уравнения для нашего мира, исходя из наблюдений и экспериментальных данных. Макс предлагает рассмотреть “Физику Наоборот” – “Physics from Scratch” – вы задаете уравнения, какой мир вы получаете?
Мы можем задать законы мира… ну, например, игры «жизнь». Можем ли мы обойтись без словесного описания? Как, например, сказать, что пространство клеточек двумерно? Через уравнения — указанием степенного закона, как быстро растет количество клеточек не дальше расстояния N. Еще пример, уравнения теории струн сходятся только, если размерность пространства равна 10, 11 или 26. Быть может, вначале сформулировать физику аксиоматически покажется сложным, но математики хорошо преуспели в создании аксиоматических теорий (и миров). Возьмите, например, аксиоматику Пеано. Это чистые формулы, там не объясняется, что такое “число”, что такое “прибавить” или “умножить”.
Описание vs Эквивалентность.
Что же мы имеем? У нас есть (будет) TOE, описывающее ВСЕ сущее.
Секунду… А что значит “описывающее”? Вот, например, механика описывает движение тел. Но мы знаем, что все это возможно благодаря куче упрощений: тела не материальные точки, есть сопротивление воздуха, трение итд. Есть формулы, которые описывают реальность, но мы знаем, что реальный мир отличается от идеального, описанного формулами.
Но в случае ТОЕ это не так: любой, абсолютно любой физический аспект реальности описывается формулами — или это не ТОЕ. В чем же разница между теорией и реальностью в данном случае, если они абсолютно эквивалентны?
Макс утверждает, что в случае ТОЕ математика не описывает реальность, а математика и есть реальность. Если вы вдруг не согласны, обратное бы означало, что есть уравнения с их решениями, есть точно такой же мир, который полностью подчиняется указанным формулам, но еще и реален. В данном случае слова “еще и реален” есть словесный багаж в чистом виде, от которого мы отказались выше, такая современная anima sola физики. Таким образом, мы вынуждены признать, что на фундаментальном уровне физика и математика – это одно и тоже.
Формулы и пламя
Макс был не первым с подобными идеями. Сам Хокинг поставил вопрос: “А что же вдыхает пламень именно в эти уравнения, создавая вселенную?” “what is it that breathes fire into the equations and makes a universe for them to describe?”

Если бы мы сказали, что наша вселенная особенная, потому что она существует, мы бы снова были бы отброшены на шаг назад, к концепции “anima sola”. Нет, ничего не вдувает пламень в наши формулы. Было бы странно, если бы все аксиоматические системы математики разбивались бы на два неравных класса: системы, для которых существуют вселенные и системы, которым не повезло. Это противоречит всей гипотезе математической вселенной.
Объяснить все это можно только так: если нет никакой anima sola, то все аксиоматические системы равны и каждой аксиоматической системе соответствует вселенная. Да, скорее всего большинство систем тривиальны, и, возможно, большинство аксиоматик не дают возможности развиться (то есть появиться в решениях) сложным, нетривиальным системам и, тем более, жизни.
“Физика наоборот” еще ждет своих будущих исследователей. Я бы дорого дал, чтобы узнать, является ли наша вселенная самой простой из тех, где возможна разумная жизнь или нет.
Ответы на некоторые вопросы
Интересно, что после первого шага (у ТОЕ нет багажа) второй шаг (математика и физика это одно и тоже) и третий шаг (каждая аксиоматика создает вселенную) были вынужденными. Вот как далеко нас завело.
А почему вселенная вообще существует?
Ответ: потому что может существовать.
Когда же возникли эти структуры и почему возникли?
Математические структуры не существуют во времени и пространстве. Они просто существуют.
Являемся ли мы эмуляцией?
Нет. Для существования математических структур не требуется никакой машины, “просчитывающей” их. Число 19 является простым вне зависимости от того, есть или нет компьютер, который все время пытается его в цикле поделить, проверяя на простоту
А это вообще, как – наука или фантазии?
Как мы можем постулировать что-то, что принципиально не можем проверить? Макс ожидает этой критики. На самом деле, это не первый раз, когда мы делаем такое. Мы давно привыкли к концепции мульти вселенной.
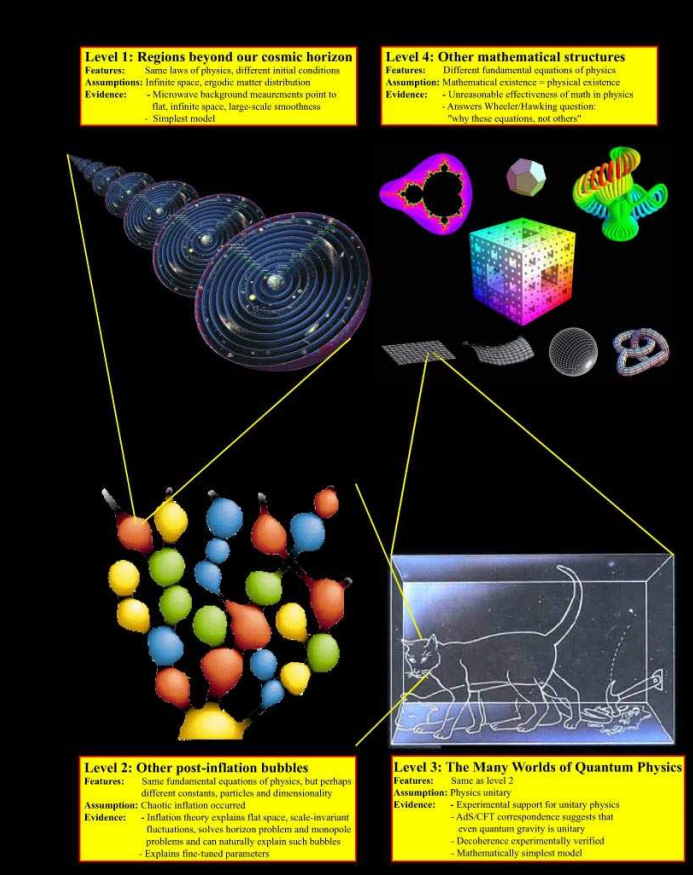
На уровне 1 мы говорим об областях Вселенной, которые так быстро удаляются от нас из-за расширения, что больше никогда не будут в каузальной связи с нами. Тем не менее, ни у одного космолога не повернется язык сказать, что там ничего нет, потому что мы туда не можем полететь
На уровне 2 мы говорим о других “пузырях” в теории eternal inflation где, возможно, при тех же законах физики другие начальные условия и другие физические константы
Уровень 3 образован альтернативными вселенными Мульти вселенной в интерпретации Эверетта. Об этом будет отдельная статья.
Мы вынуждены принять существование уровня 4, соответствующего другим математическим вселенным, которые нам только предстоит изучать (теоретически)
Источник
