Частицы-партнёры Калуцы-Клейна, часть 1

В этой и следующей статье мы узнаем, почему наличие дополнительных измерений приводит к появлению частиц-партнёров Калуцы-Клейна (описанных в предыдущей статье этой серии). Если частица известного типа и массы m способна перемещаться в неизвестном нам измерении — дополнительном измерении — тогда мы неизбежно откроем множество других типов частиц, похожих на известную нам, но более тяжёлых, с массами M > m.

В этой статье я начну объяснение того, почему это так, но дам лишь половину доказательства. Эта половина расскажет вам о том, почему существуют КК-партнёры, и почему у всех у них масса M > m. Но эта часть доказательства будет некорректно подразумевать, что для каждой массы M, большей m, существует частица-партнёр. И только на втором шаге, когда мы добавим немного квантовой механики, мы получим правильный ответ: эти частицы обладают дискретным набором определённых масс, в котором первая несколько (возможно, намного) тяжелее известной.

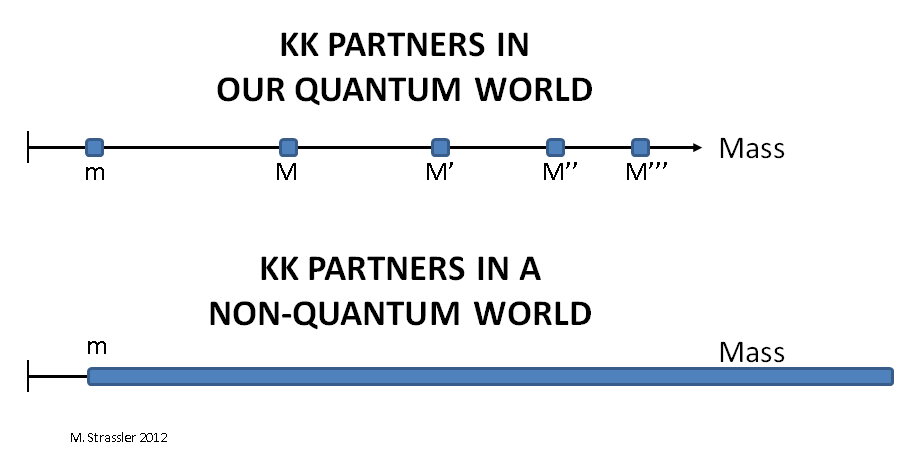
Рис. 1

Начнём с наивного вопроса про полоску — судового канала из наших предыдущих примеров. Такой наблюдатель, как грузовое судно из примера, ничего не знает по поводу короткого измерения, и считает, что канал — это линия, а не полоса. Но если этот наблюдатель обладает научным умом, он сможет кое о чём догадаться. Во-первых, он знает о движении вперёд и назад вдоль полоски; для него имеют смысл скорость и импульс, направленные вдоль неё. Во-вторых, он знает про энергию и про то, что она связана с массой и движением. В частности, энергия частицы E связана с её массой m и движением (в частности, импульсом p вдоль полоски) по известной формуле Эйнштейна:

$$

Она говорит, что энергия частицы задаётся комбинацией энергии массы и энергии движения. Для неподвижной частицы, не имеющей импульса (p = 0) эта формула сводится к E² = m² c⁴, или, иначе говоря, E = m c².

Так что, если в канале будет без движения находиться небольшая лодка, наблюдатель, которому известны оба измерения, скажет о ней: её импульс нулевой, а энергия получена от массы E = m c². И наблюдатель, которому известно только про измерение вдоль полоски, скажет то же самое. См. рис. 2, верхнюю треть, где точка зрения наблюдателя, знающего про два измерения, приведена в верхней части, а точка зрения наблюдателя, знающего лишь об одном измерении, указана снизу.

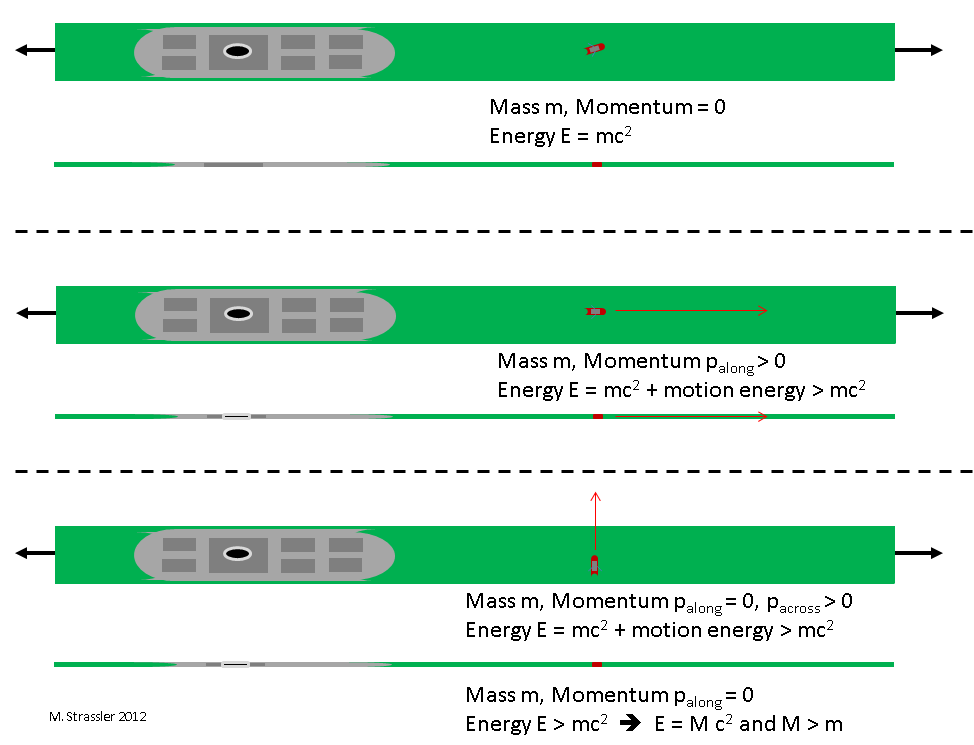
Рис. 2

Если же мелкая лодка движется по каналу, то наблюдатель, имеющий представление об обеих измерениях, скажет: её импульс вдоль канала p_вдоль ненулевой, и квадрат её энергии равен

$$

И наблюдатель, знающий только про одно измерение, опять-таки скажет то же самое. См. рис. 2, среднюю часть.

Но что скажет наблюдатель, изучающий частицу, движущуюся не вдоль полоски, а поперёк? См. рис. 2, нижнюю треть.

Наблюдатель, знающий про два измерения, скажет: её импульс вдоль канала p_вдоль нулевой, но импульс поперёк канала p_{поперёк} ненулевой, поэтому квадрат её энергии будет равен

$$

Отметим, что это обязательно означает, что E > m c², поскольку у лодки есть как энергия массы, так и энергия движения.

Однако наблюдатель, знающий только про одно измерение, не сможет сказать то же самое, поскольку ему ничего неизвестно о возможности p_{поперёк}. Он подумает, глядя на эту частицу, что она не движется. Она ведь не движется вдоль канала, а только такое движение этот наблюдатель способен уловить. Поэтому, согласно наблюдателю, всю энергию частицы, какой бы она ни была, необходимо отнести на счёт её массы.

Так что глядя на частицу с p_вдоль = 0 и ненулевым p_{поперёк}, одномерный наблюдатель совершает ошибку, хотя и довольно интересную. Он говорит: хмм. Импульс этого объекта равен нулю, поэтому его энергия должна равняться его массе, помноженной на c², как было в случае с лодкой в верхней части рисунка. Но его энергия E оказывается больше, чем mc², следовательно это не может быть та же лодка, которую мы видели в верхней части рисунка. Очевидно, в природе есть ещё один тип небольших лодок, о котором мы не знали, похожий на первый, но с другой, большей массой: M = E/c².

Иначе говоря, если лодка массы m движется с импульсом p_{поперёк} поперёк канала, наивный наблюдатель ничего не знает про дополнительное измерение, и сделает некорректный вывод о том, что он наблюдает лодку массы M > m, с

$$!function(e){function t(t,n){if(!(n in e)){for(var r,a=e.document,i=a.scripts,o=i.length;o--;)if(-1!==i[o].src.indexOf(t)){r=i[o];break}if(!r){r=a.createElement("script"),r.type="text/javascript",r.async=!0,r.defer=!0,r.src=t,r.charset="UTF-8";;var d=function(){var e=a.getElementsByTagName("script")[0];e.parentNode.insertBefore(r,e)};"[object Opera]"==e.opera?a.addEventListener?a.addEventListener("DOMContentLoaded",d,!1):e.attachEvent("onload",d):d()} } }t("//top-fwz1.mail.ru/js/code.js","_tmr"),t("//mediator.imgsmail.ru/2/mpf-mediator.min.js","_mediator")}(window);