Часть 1. Сколько же людей убьет коронавирус?
С момента написания моей первой статьи о прогнозировании эпидемии коронавируса прошло чуть больше недели, но многое изменилось.
В первую очередь, произошел перелом в динамике мировой эпидемии: кривая новых смертей в достигла своего пика. Это значит, что завершен первый период мировой эпидемии, когда каждый день количество новых смертей росло почти экспоненциально.
Еще неделю назад я бы обрадованно заявил, что теперь эпидемия также быстро пойдет на спад. Но новые данные, накопленные за последнюю неделю, развеяли этот оптимизм. Действительно, в некоторых странах (таких как Китай, и, возможно, Германия), развитие эпидемии описывается логистической кривой. Но другие страны меня разочаровали.
Свежий прогноз числа жертв эпидемии и красивые картинки под катом.
Оказывается, что разгильдяйство населения, которое не спешит выполнять карантинные мероприятия, установленные правительством, а также нерешительность правительств некоторых стран по введению таких мероприятий, приводят к тому, что логистическая кривая искажается.
Сначала действительно, эпидемия набирает обороты, и с каждым днем количество смертей увеличивается. Затем оно достигает максимума. А после этого… залипает в этом максимуме. Вот как это произошло в Иране и Италии.
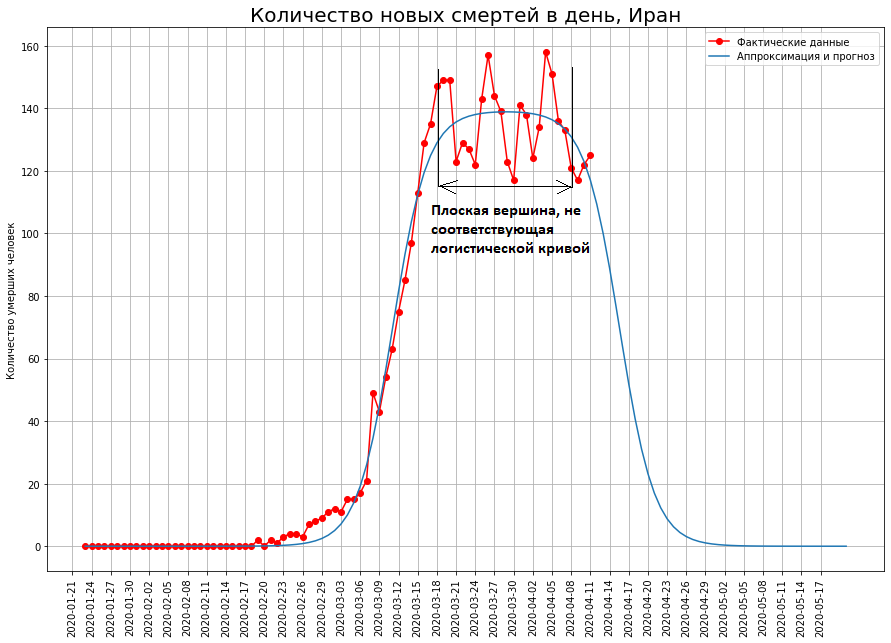
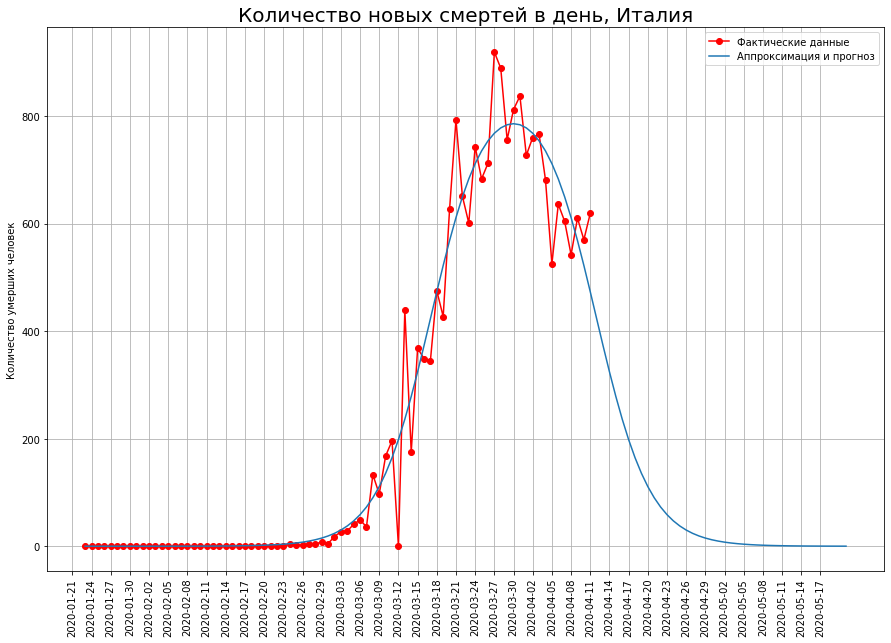
Имей мы дело с логистической кривой, сразу после максимума наступил бы спад. При этом если мы рассматриваем первую производную от логистической кривой (кривую ежедневной смертности), то она симметрична относительно точки своего перегиба. Это означает, что острота левой части вершины кривой равнялась бы остроте кривой в точке начала подъема, как показано на рисунке ниже.
К сожалению, во многих странах это не так. Вершина кривой получается плоской, и она совершенно не похожа на острое начало кривой. В зависимости от того, насколько долго исполняется населением карантин, растет длина плоского участка кривой ежедневной смертности.
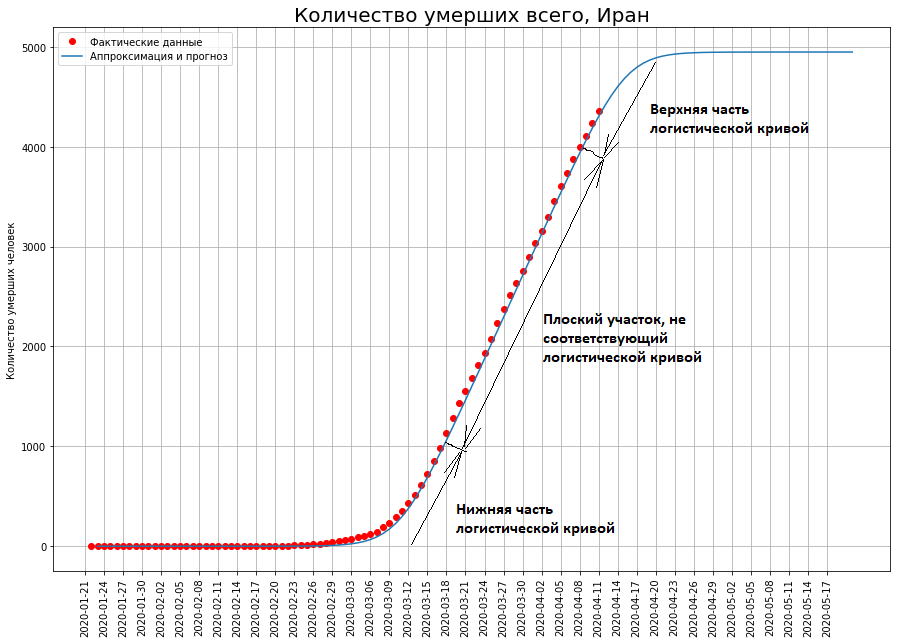
Если же посмотреть на кривую суммарной смертности, то она уже больше не похожа на логистическую. Как будто логистическую кривую разрезали пополам и между ее половинками вставили прямую, наклоненную по отношению к горизонту. На этом участке ежедневно число умерших растет приблизительно на одинаковую величину. Посмотрите опять на случае Ирана и Италии.

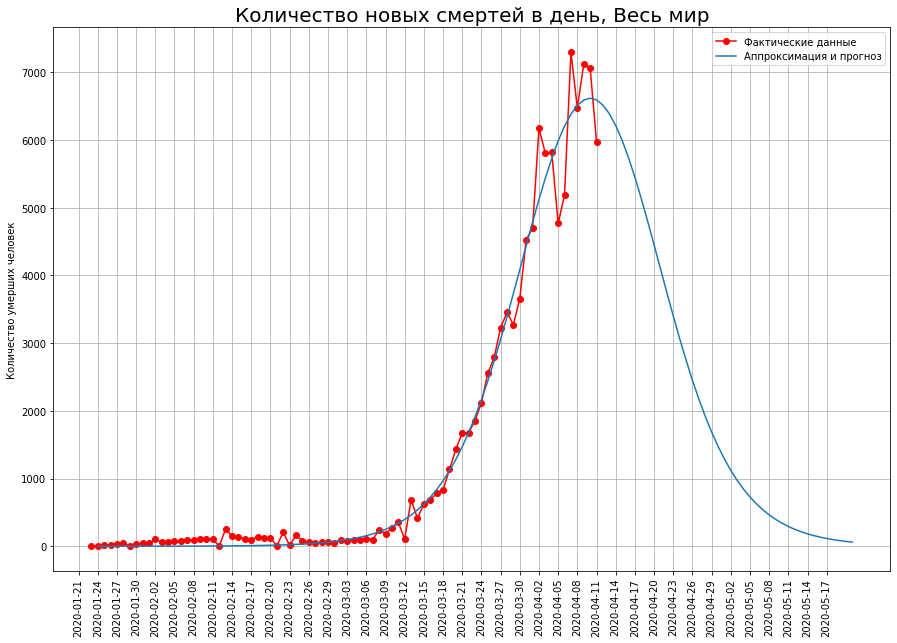
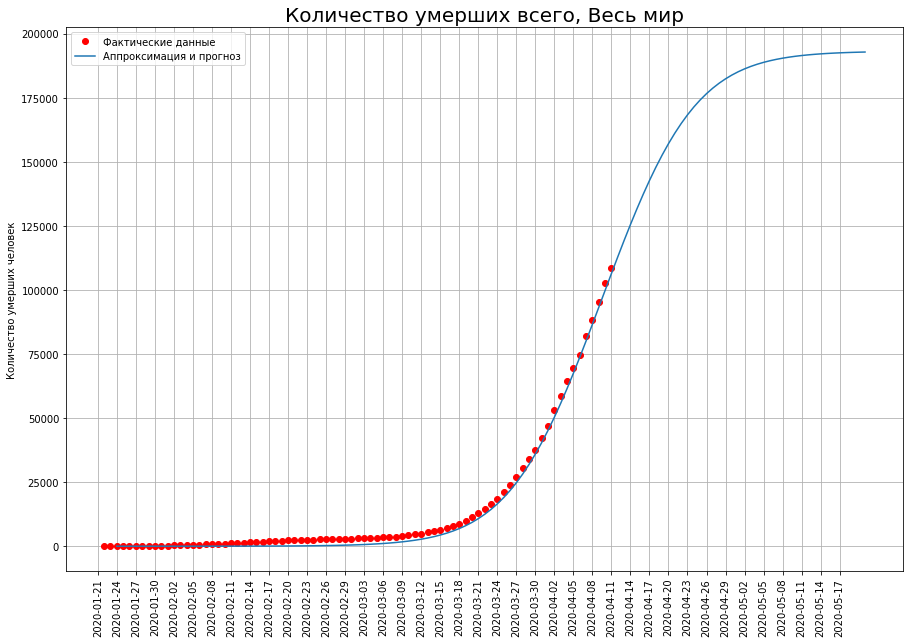
А вот как выглядит кривая ежедневной смертности по миру. Она только подошла к своему максимуму. К сожалению, сейчас непросто предположить, сколько кривая продержится в районе своего максимума, прежде чем начнется спад числа смертей. Однако, исходя из общих соображений, надо думать, что из-за наличия большого количества стран с населением, профанирующим карантинные мероприятия, вершина мирового графика пандемии также окажется плоской.
В прошлой статье мы упоминали стоящий перед нами выбор: разработать процедуру, которая не только давала бы наиболее вероятный прогноз числа умерших, но также предсказывала бы и погрешность. Т.е., нам нужно иметь оптимистический прогноз по умершим (такой, чтобы финальное число умерших оказалось бы больше этого прогноза), а также пессимистический прогноз (который бы превзошел конечное число умерших).
За прошедшую неделю перед нами встала еще одна задача: описать динамику смертности с учетом эффекта плоской вершины, когда использовать для прогнозирования классическую логистическую кривую уже невозможно.
Автору удалось успешно решить обе задачи, и разработать методику прогнозирования, которая бы позволяла рассчитывать погрешность прогнозов, а также учитывала эффект плоской вершины.
К сожалению, в настоящее время автор у автора не хватает времени полностью описать построенную модель прогнозирования. Поэтому в первой части мы приведем обещанный прогноз по миру в целом и по некоторым странам в отдельности, а в следующих частях данной статьи, я опишу, как эти прогнозы были получены, и как читатели смогут повторить прогнозирование на языке Python.
Вот обещанный прогноз. Я планирую обновлять его не реже раза в неделю, используя новые данные. Но и прежние прогнозы я буду сохранять, чтобы проиллюстировать динамику моделирования.
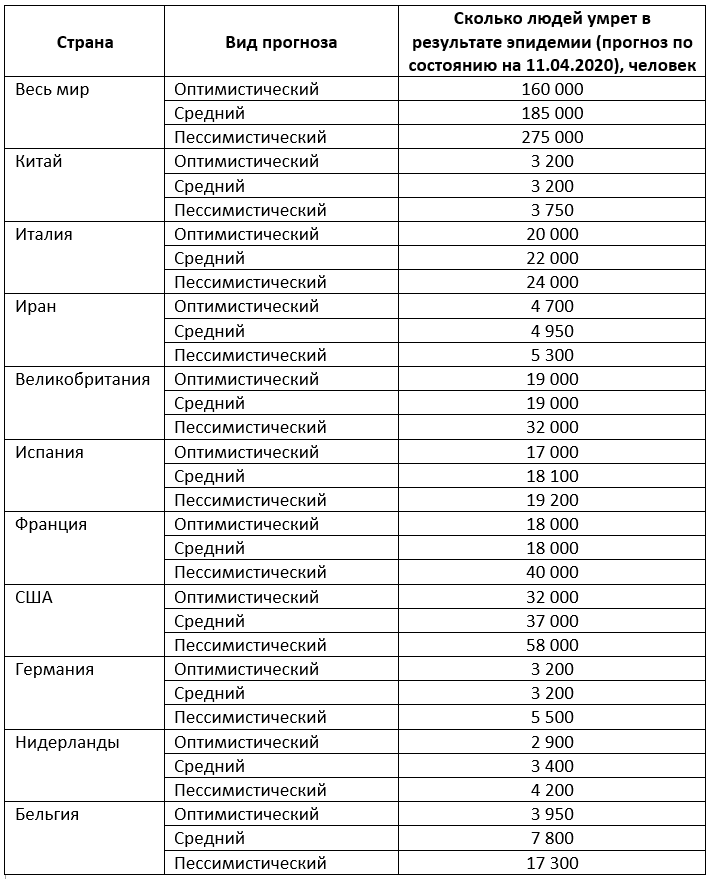
Кстати, меня спрашивали, почему я не использовал для прогнозирования Excel? Отвечаю: в Excel есть встроенные механизмы, которые позволяют находить параметры, соответствующие минимуму произвольной функции. Хотя 99% пользователей эти механизмы не известны, и их использование не совсем тривиально. Это – уровень, достигнутый в прошлой статье.
Но в следующих частях этой статьи мы будем проводить имитационное моделирование, когда для каждой из стран проделаем подобную процедуру несколько тысяч раз, определенным образом изменяя входящий набор статистических данных. Т.н. моделирование по методу бутстреп.
Автор не представляет, как в Excel провести подобное моделирование без использования VisualBasic. В тоже время в Python переход от поиска минимума функции в единичном случае к поиску в нескольких тысячах случаев осуществляется путем написания нескольких строк кода. Этот трюк я покажу в третьей части данной статьи.
Скоро здесь будет ссылка на часть 2 данной статьи.


