«Прекрасно то, чего нет» (Жан-Жак Руссо)
«Наука приносит пользу только тогда, когда говорит вам о еще не поставленных экспериментах. Она никому не нужна, если позволяет судить лишь о том, что известно из опыта, что только что произошло» (Ричард Фейнман)
«Учёные делают великие открытия лишь потому, что выдвигают гипотезы и проводят эксперименты. Неудача следует за неудачей, но они не отступают, пока не добиваются тех результатов, которые им нужны» (Эдвин Герберт Лэнд)
От философов-антиреалистов, эзотериков и богословов часто можно услышать проповеди на тему ограниченности научных методов и о существовании за пределами физического мира иных планов бытия, которые нематериальны и не могут быть познаны экспериментальным путём. Но они не в курсе, что наука уже много лет занимается изучением контрфактуалов — «потусторонних» событий, происходящих не в нашей вселенной, но тем не менее подчиняющихся известным физическим законам. Учёные постоянно открывают новые способы «взломать» классическую физику и ставят умопомрачительные эксперименты, результаты которых заставляют нас пересмотреть традиционные определения реальности. Практика показывает, что природа познаваема и содержит в себе всё необходимое для роста знания, главное – задавать ей правильные вопросы. Как измерить светочувствительную бомбу, не подрывая её? Как провести вычисление, не включая компьютер? Как увидеть, не глядя, и узнать о событии, которое не произошло? Как подсмотреть за котом Шрёдингера и воскресить его? Как отменить коллапс волновой функции? Наконец, как осуществить настоящую телепортацию без локального обмена информацией? Если обычная квантовая телепортация, запутанность и туннелирование уже не кажутся вам чем-то удивительным, готовьтесь к настоящим чудесам. В этой статье я разберу пять экспериментов, о которых вы вряд ли слышали, но результаты которых действительно взрывают мозг.
Возможно, кому-то при упоминании бесконтактных измерений первыми на ум приходят такие непотребства, как телекинез, бесконтактный массаж и бесконтактный бой. Я не буду здесь напоминать, почему подобные сверхспособности невозможны – это понимает каждый, кто усвоил школьный курс физики. Речь пойдёт совсем о другом. Эффект наблюдателя, как вы помните из одноимённой статьи, состоит в том, что невозможно измерить квантовую систему, не изменив её состояния. Это правило действительно универсально, только в нём есть лазейка, позволяющая измерить систему косвенно или так, чтобы процесс можно было обратить вспять и повторить заново. Изучением бесконтактных измерений, при которых не происходит физического взаимодействия частиц, с 90-х гг. активно занимается израильская школа физиков-теоретиков, представленная Якиром Аароновым, Авшаломом Элицуром и Львом Вайдманом. На сегодняшний день это одно из самых актуальных направлений в теоретической физике, и скоро вы узнаете, почему.

Бесконтактное измерение часто путают со слабым измерением, хотя бесконтактное измерение может быть и «сильным», а слабое измерение – «контактным». При слабом измерении измерительный прибор косвенно взаимодействует с измеряемым объектом, поэтому коллапса волновой функции или расщепления миров не происходит. Например, в квантовом компьютере с помощью магнитного импульса можно «подсмотреть» состояние кубита. При этом его волновая функция «частично коллапсирует», т.е. вероятности смещаются в сторону более вероятного состояния. Если результат вам не понравится, вы инвертируете кубит в противоположное состояние и снова косвенно измеряете его, смещая соотношение вероятностей к исходному значению. Такую процедуру можно провести много раз, приближая вероятность получения нужного результата к 100%. Этот приём был назван в честь древнегреческого философа Зенона Элейского, автора знаменитых апорий – парадоксов, с помощью которых он доказывал невозможность движения. Квантовый эффект Зенона, впервые предсказанный Аланом Тьюрингом ещё в 1954 г., заключается в том, что квантовое состояние частицы не изменяется, если часто её измерять. Например, при постоянном измерении нестабильная частица никогда не распадётся.
Квантовый тестировщик бомб Элицура-Вайдмана, или парадокс квантового тральщика
В 1993 г. Авшалом Элицур и Лев Вайдман предложили мысленный эксперимент, позволяющий измерить бомбу без взаимодействия с ней. Представьте, что вам дали целую кучу бомб, среди которых есть настоящие, а есть фальшивые. Вам нужно определить, какие бомбы действующие, но на каждой бомбе установлен фотодетектор, при попадании единственного фотона подрывающий настоящую бомбу или пропускающий фотон сквозь себя, если бомба фальшивая. Казалось бы – миссия невыполнима. Но квантовая физика даёт вам шанс идентифицировать по крайней мере четверть бомб, не подрывая их. Этот способ называется бесконтактным измерением.
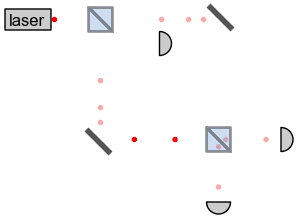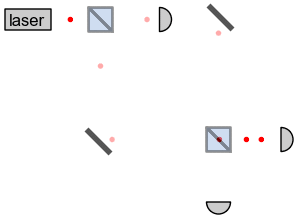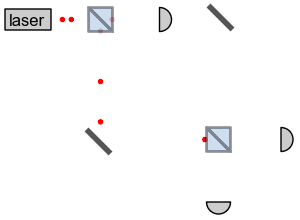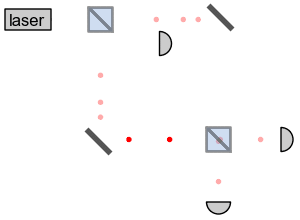
В эксперименте используется интерферометр Маха-Цендера, который я уже показывал при описании эксперимента «квантовый ластик с отложенным выбором» в статье «Эффект наблюдателя». Источник света выпускает по одному фотону на полупрозрачное зеркало, отражающее или пропускающее фотон с вероятностью 50/50. На каждом пути стоит обычное зеркало, направляющее фотон к ещё одному полупрозрачному зеркалу. Там пути пересекаются, фотон интерферирует сам с собой и принимает исходное направление, попадая в итоге на детектор D2. Попаданию фотона на детектор D1 препятствует деструктивная интерференция. Определить, по какому пути прошёл фотон, невозможно, поэтому считается, что он проходит одновременно через оба плеча, т.е. находится в суперпозиции.
Здесь у многих возникает вопрос: почему взаимодействие фотона с детекторами считается измерением, а его взаимодействие с зеркалами – нет? Ответ состоит в том, что при попадании фотона на детектор информация о столкновении записывается в состоянии измерительного прибора и передаётся дальше, а при столкновении с зеркалом этого не происходит. Вообще, когда фотон отражается от зеркала, у него изменяется импульс, а закон сохранения импульса требует, чтобы импульс зеркала изменился на равную и противоположную величину. Это значит, что одно из зеркал начнёт вибрировать с немного большей или меньшей энергией, и по измерению этих вибраций можно будет узнать, по какому пути прошёл фотон. Но зеркало – макроскопический объект, постоянно взаимодействующий с окружающей средой и испытывающий тепловые флуктуации. Его совокупная энергия принимает огромное число возможных значений вокруг среднего, «классического». Увеличение энергии зеркала на один квант из-за отражения от него фотона просто затеряется на фоне этого шума и никак не отразится на макросостоянии зеркала. Только в одном случае из триллиона триллионов фотон может запутаться с одним из зеркал, оказав на него заметное воздействие. Но на практике вероятность такого события намного ниже, чем вероятность разрушения интерференции из-за неточности измерительных приборов, поэтому ею можно смело пренебречь.
Итак, по общему правилу, когда макроскопический объект вроде зеркала подвергается незначительному воздействию, запутанности не возникает, и этот объект остаётся совершенно незатронутым. Но если на нижнее зеркало или на нижнее плечо интерферометра поместить бомбу, она точно будет служить измерительным прибором, определяющим, по какому пути прошёл фотон. По условиям эксперимента, действующая бомба должна поглощать фотон и не давать ему пройти дальше, иначе фотон вызовет интерференцию прежде, чем взрывная волна будет зафиксирована детектором, что исказит статистику результатов измерений. Если бомба настоящая, интерферометр не работает. Тогда фотон либо с вероятностью 50% проходит по нижнему плечу и взрывает бомбу, либо проходит по верхнему плечу, попадает на второе полупрозрачное зеркало и с вероятностью 50/50 направляется к детекторам D1 и D2. Если же бомба фальшивая, интерферометр работает, фотон проходит через оба плеча, интерферирует сам с собой и попадает только на детектор D2.
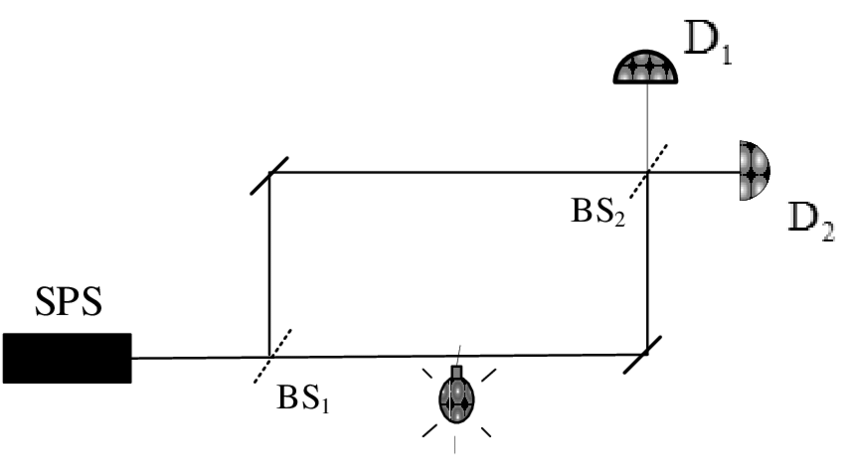
По итогам эксперимента в 50% случаев бомба взорвётся, в 25% случаев фотон попадёт на детектор D2 и в 25% случаев фотон попадёт на детектор D1. Если срабатывает детектор D2, это значит, что с 75%-вероятностью бомба неисправна и с 25%-вероятностью – исправна. Но если срабатывает детектор D1, это со 100%-вероятностью говорит нам о том, что бомба исправна: фотон прошёл по верхнему плечу интерферометра и не взорвал её. Таким образом, эксперимент позволяет идентифицировать 25% бомб, при этом 50% взорвутся, а ещё 25% останутся неопределёнными. Авторы эксперимента, Элицур и Вайдман, видят в нём подтверждение многомировой интерпретации квантовой механики, ведь мы по сути узнаём о событии (взрыв бомбы), которое не произошло в нашей вселенной, но произошло в параллельной. С ними согласны не все физики, однако альтернативные интерпретации не объясняют, откуда в сознании наблюдателя берётся информация об исправности бомбы.
В 1994 г. Пол Квят из университета в Инсбруке и Томас Герцог из Женевского университета подтвердили предсказания Элицура и Вайдмана на практике, используя вместо бомбы обычное зеркало. Затем они усложнили интерферометр добавлением ещё четырёх зеркал и добились распознавания «бомбы» в 50% случаев. Но и это был ещё не предел. Уже в 1996 г. была предложена усовершенствованная версия эксперимента, в которой процент идентифицированных бомб приближается к 100%. Идея состоит в том, чтобы отразить фотон от зеркала с пропускающей способностью 1/99, за которым находится бомба, а затем воссоединить два направления, чтобы фотон проинтерферировал сам с собой, если бомба фальшивая. Пройдя через такой зеркальный резонатор со множеством бомб, фотон идентифицирует их все с минимальной вероятностью взрыва благодаря квантовому эффекту Зенона. 10 лет спустя группе японских учёных удалось бесконтактным способом обнаружить до 88% объектов, которых не коснулся ни один фотон.

Как вы уже наверняка догадались, интерферометр Маха-Цендера можно использовать не только для тестирования бомб. Вот и физики вскоре задумались: а что, если заменить бомбу компьютером?
Контрфактические вычисления, или как получить ответ, не задавая вопрос
Идею контрфактических вычислений впервые предложили физики Грэм Митчисон и Ричард Йожа. В 1997 г. Кит Боуден из исследовательского отдела теоретической физики Биркбек-колледжа Лондонского университета опубликовал статью «Классическое вычисление может быть контрфактическим», или «Может ли кот Шрёдингера коллапсировать волновую функцию?». Он описал цифровой компьютер, который можно было бы подвергнуть контрфактическому опросу, чтобы вычислить, сможет ли луч света пройти через лабиринт зеркал. В этом эксперименте также используется интерферометр Маха-Цендера, но вместо бомбы устанавливается зеркальная решётка, которая определяется битовой матрицей размера n на n – классификатор битовых строк. Выходной сигнал (сбой или нет) сам по себе определяется одним битом. Таким образом, зеркальная матрица представляет собой цифровой компьютер с n-квадратным входом и 1 битом на выходе. С вероятностью ¼ фотон попадает на детектор и сообщает о том, что лабиринт непроходим, не проходя этот лабиринт фактически. Интерферометр в целом представляет собой квантовый компьютер, а его часть с лабиринтом зеркал – полуклассическая, но тестируется контрфактическим способом, т.е. без фактического запуска.
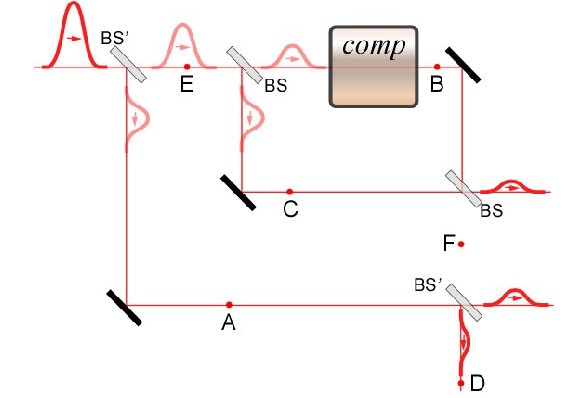
В 2015 году контрфактические квантовые вычисления были продемонстрированы китайскими учёными в эксперименте на «спинах отрицательно заряженной азотной вакансии в алмазе». Ранее предполагаемые пределы эффективности были превышены, в результате чего была достигнута противоречащая фактической вычислительная эффективность 85% при более высокой эффективности, предусмотренной в принципе. Это значит, что контрфактические квантовые вычисления реально работают как метод вывода результата вычисления без фактического запуска квантового компьютера. Квантовый компьютер устанавливается в суперпозицию состояний «не работает» и «работает» с помощью квантового эффекта Зенона и квантовой интерференции. После многих повторений очень быстрых измерений состояние «не работает» переходит к окончательному значению, записанному в свойствах квантового компьютера. Измерение этого значения позволяет узнать результат некоторых типов вычислений, таких как алгоритм Гровера.
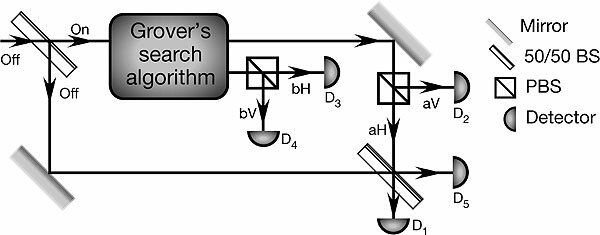
Естественно, экспериментальная реализация схемы Боудена порождает множество воспросов. Можно ли масштабировать контрфактические вычисления и применить их с пользой на практике? Каким будет результат бесконтактного измерения кота Шрёдингера или друга Вигнера, если поместить их на место бомбы? Если наблюдатель может бесконтактно измерять бомбу, тогда что мешает с помощью бомбы бесконтактно измерить наблюдателя (друга Вигнера)? Это всё равно что получить от человека ответ, не задавая ему вопрос. Или получить результат работы, которую он не делал. Или подключить интерферометр к терминалу фондового рынка и протестировать мировую финансовую систему. Может, вообще любую работу можно осуществлять контрфактически? Пусть за нас трудятся наши двойники из параллельных вселенных, а мы будем отдыхать. Красота!
К сожалению, такой сценарий вряд ли реализуем. В своей статье Кит Боуден детально рассмотрел, какие типы вычислений можно провести контрфактическим способом. «Одним критерием является то, что вычисления должны быть обратимыми, то есть после выполнения вычислений должна быть возможность вернуть систему в исходное состояние или хотя бы в такое, в котором она (в принципе?) неотличима от своего первоначального состояния. Очевидно, что это справедливо для зеркальной решётки, не претерпевающей изменений в ходе вычислительного процесса. Это также верно и для класса квантовых компьютеров, поскольку квантовые вычисления определяются унитарным преобразованием». Вообще в контрфактическом вычислении нет ничего необычного, если рассматривать устройство целиком, вместе с интерферометром, как квантовый компьютер: «Хотя вычисления являются классическими, общая установка, включая измерительное устройство, представляет собой квантовый компьютер, и наш результат по сути является частным случаем алгоритма Йожи, который показывает, что все квантовые вычисления могут быть проведены контрфактически».
А что насчёт классических вычислений? Согласно постулату квантовой механики об измерении, при измерении вектор состояния (волновая функция) коллапсирует в один из собственных векторов (функций) оператора измеряемой величины. Измерение — это не взаимодействие, а получение наблюдателем информации о системе. Если вы можете сказать, какой путь прошла частица, интерференция не происходит. Когда компьютер работает, он выделяет тепло, что служит индикатором независимо от того, вызвал ли электрон реальное вычисление. Но второй закон термодинамики можно и обойти следующим образом: «создать устройство такого типа, что классический компьютер всегда работает и что присутствие фотона запускает передачу определенного входного сигнала на вычислительный процесс, а не запуск самого процесса. В этой схеме вычисление должно быть логически обратимым, но не обязательно термодинамически обратимым. Требуется только чтобы термодинамические процессы были симметричны относительно 1 и 0, т.е. они должны потреблять одинаковое количество энергии независимо от того, в каком состоянии находится бит или в какую сторону он переключается».
Большинство процессов в нашем мире термодинамически необратимы, т.е. подчиняются второму закону термодинамики. Следовательно, подключив к интерферометру вместо бомбы любой более-менее сложный макроскопический объект, включая кота Шрёдингера, мы ничего не добъёмся – он запутается с окружающей средой быстрее, чем мы успеем его измерить. Протестировать таким образом человека тоже вряд ли получится, но теоретически можно проверить, насколько наше мышление детерминировано и влияют ли на него квантовые эффекты. А если вместо кота Шрёдингера использовать настоящую бомбу? Скажем, сработает бомба или нет, будет определяться тем, распадётся или нет помещённый внутрь неё радиоактивный атом? Ну, есть и более безопасный вариант: заменить бомбу квантовым генератором случайных чисел. Этого будет достаточно, чтобы создавать квантовый шум из событий, которые никогда не происходят.
Если же говорить о более полезных способах применения идеи, то теоретически возможны технологии контрфактической фотографии, голографии, криптографии и телепортации. Но в любом случае о нарушении законов сохранения энергии или информации речь не идёт, всё объясняется в рамках существующих физических теорий. С помощью квантового эффекта Зенона долю «успешных» испытаний (тех, в которых вычисления не происходят, хотя получен результат вычислений) можно сделать произвольно большой, но время, необходимое для получения результата, такое же, как и то, что понадобится для проведения вычислений. То есть никаких преимуществ в скорости контрфактические вычисления не дают. Но они могут быть интересны в обстоятельствах, когда есть причина не проводить вычисление (например, вероятность того, что оно навсегда изменит компьютер), но мы всё равно хотим знать результат.
Парадокс Харди, или как узнать о том, чего не было
Ещё один способ бесконтактного измерения был предложен в 1992-1993 г. Люсьеном Харди и получил название «парадокс Харди». В этом мысленном эксперименте используется два пересекающихся интерферометра Маха-Цендера, а вместо фотонов – противоположно заряженные частица и античастица, например, электрон и позитрон. Электрон движется по нижнему интерферометру, позитрон – по верхнему. Если интерферометры рабочие, каждый из них расщепляется на первом полупрозрачном зеркале (BS1), проходит одновременно по двум путям и интерферирует сам с собой на втором полупрозрачном зеркале (BS2), после чего попадает на детектор С. Но проблема в том, что в точке Р интерферометры пересекаются, электрон с позитроном сталкиваются и аннигилируют, что аналогично бомбе в эксперименте Элицура-Вайдмана. Это происходит с вероятностью 25%. Впрочем, как электрон, так и позитрон могут пройти по другому пути (О) и с вероятностью 50/50 попасть на детекторы C или D. Таким образом, при срабатывании детекторов D мы узнаём об аннигиляции, которая не произошла.
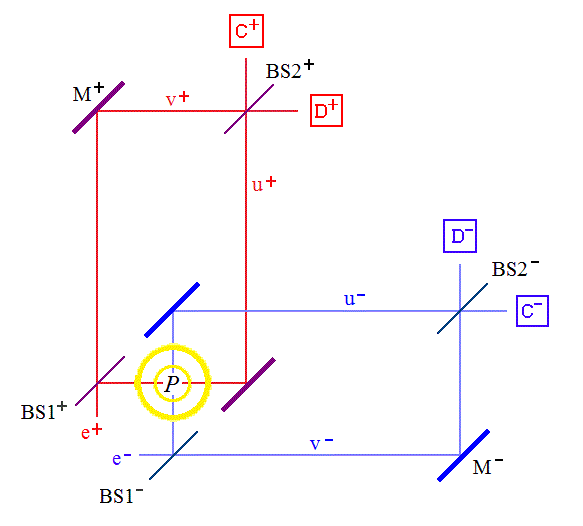
Эксперимент Харди даёт следующую статистику: с вероятностью 1/16 сработают детекторы C- и D+, с вероятностью 1/16 – детекторы C+ и D-, с вероятностью 9/16 – детекторы С+ и С-, с вероятностью 1/16 – детекторы D+ и D-, а с вероятностью 4/16 произойдёт аннигиляция. Также существуют версии эксперимента Харди с тремя и более частицами, в которых вероятность наблюдения контрфактического события доходит до 25%. На практике в 2009 г. был реализован похожий эксперимент с поляризованными фотонами, подтвердивший предсказания Харди. Эксперимент исключает теорию локальных скрытых параметров и требует признания квантовой контекстуальности или нелокальности.

Эксперимент Реннингера с отрицательным результатом, или как сколлапсировать волновую функцию наполовину
В 1953 г. немецкий физик Маурициус Реннингер придумал мысленный эксперимент, наглядно иллюстрирующий проблему квантового измерения. В формулировке 1960 г. он выглядит так. У нас есть пара полусферических детекторов со 100-процентной эффективностью, полностью окружающих расположенный по центру радиоактивный атом. При распаде атом излучает альфа-частицу, которая попадёт или на один, или на другой детектор, но никак не на оба сразу. Предположим, что полусферы имеют разный диаметр: меньшая находится близко к атому, а бОльшая удалена на приличное расстояние. Тогда ненаблюдение частицы ближним детектором является бесконтактным измерением, предшествующим её измерению дальним детектором: если ближний детектор не сработал, мы можем быть уверены, что сработает дальний. Но это будет частичное, или слабое измерение.
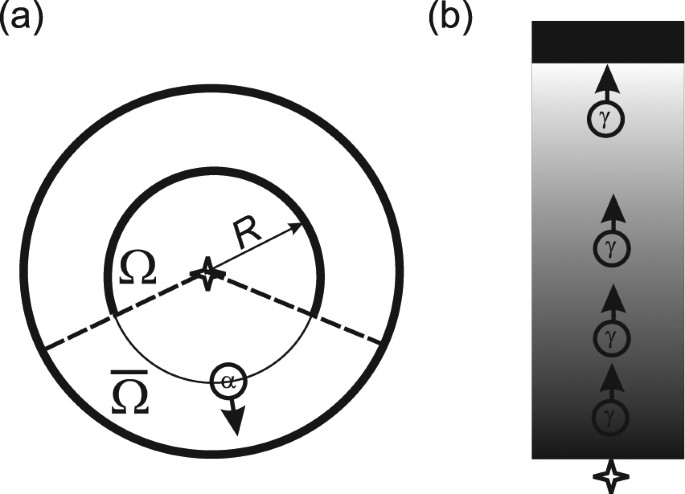
С точки зрения копенгагенской интерпретации, несрабатывание ближнего детектора означает частичный коллапс волновой функции атома. Первоначально сферическая волновая функция доходит до ближнего детектора и с вероятностью 50/50 оставляет на нём след. Если след остался, она коллапсирует полностью, если нет – волновая функция «схлопывается» наполовину и принимает форму полусферы, пока не достигнет дальнего детектора, который гарантированно сработает. Отсюда следует два вывода: а) коллапс волновой функции может быть неполным и б) коллапс волновой функции может происходить без прямого взаимодействия с измерительным прибором. В многомировой интерпретации всё проще: никакого коллапса не происходит, в половине миров срабатывает ближний детектор, в оставшейся половине – дальний. В любом случае этот опыт в очередной раз заставляет нас отказаться от идеи скрытых параметров (альфа-частица не имеет локальной траектории) и выбирать между нелокальностью или нереальностью измерения.
Сейчас эксперимент Реннингера упростили до банального расщепления фотона на полупрозрачном зеркале (BS) и его регистрации двумя детекторами, расположенными на разном расстоянии. Смысл остаётся тот же: если детектор D1 не срабатывает, мы можем быть уверены, что сработает детектор D2. Это полное бесконтактное измерение. Если же подключить к детектору D1 лампочку, а детектор D2 заменить поляризатором, получится слабое измерение. Аналогичный результат можно получить в эксперименте с тремя щелями. Допустим, фотон проходит через перегородку с тремя щелями. Если за каждой из щелей стоит детектор, один из них сработает, и мы узнаем, через какую щель прошёл фотон. Но можно поставить детектор только за одной щелью. Если он сработает, значит фотон прошёл через соответствующую щель. Но если он не сработал, значит, фотон прошёл через другие две щели одновременно. То есть мы провели слабое бесконтактное измерение, из-за которого часть волновой функции коллапсировала, а часть прошла дальше и оставила на экране интерференционную картину.
Контрпортация, или как вернуть к жизни кота Шрёдингера
В 2006 г. Александр Коротков и Эндрю Джордан опубликовали статью с заголовком «Отмена коллапса волновой функции посредством отмены квантового измерения». В 2008 г. группа Надава Каца реализовала эту идею на практике. Учёные поместили кубит в суперпозицию высоко- и низкоэнергетического состояний и получали информацию о нём с помощью слабого измерения магнитных полей. От этого кубит частично коллапсировал в сторону измеренного состояния. Если оно оказывалось нулевым, физики отменяли коллапс посредством магнитного импульса, переводившего кубит в прямо противоположное состояние, а затем снова проводили слабое измерение. По итогу трёх операций кубит возвращался в исходное чистое состояние, что позволяло попробовать провести процедуру ещё раз, чтобы добиться нужного результата измерения. Это как если бы мы могли «подсмотреть» за состоянием кота Шрёдингера, и, если он скорее мёртв, чем жив – отменить измерение, стереть полученную информацию и вернуть его в исходную суперпозицию.
При чём здесь квантовая телепортация? А вот при чём. Как я уже рассказывал в статье «Жуткое дальнодействие», квантовая запутанность не позволяет передавать информацию быстрее скорости света, потому что оба наблюдателя при измерении своей частицы получают случайный результат. Но если вместо частиц у них будет два запутанных кубита, а Алиса проведёт слабое измерение, она сможет измерять свой кубит несколько раз, не разрушая запутанность, пока не получит нужное состояние. Тем самым она передаст Бобу информацию без посредничества третьей частицы, которую нужно перемещать физически с конечной скоростью, как при обычной квантовой телепортации. Слабое измерение и квантовый эффект Зенона позволяют реализовать настоящую телепортацию! Однако Алисе и Бобу всё же придётся перед началом эксперимента распределить между собой пары запутанных частиц, синхронизировать часы и проводить измерения по заранее подготовленному расписанию. Алисе достаточно будет 10 попыток, чтобы к нужному моменту добиться нужного ей результата измерения с вероятностью 1023/1024.

В 2013 г. Хатим Салих из Национального центра математики и физики Саудовской Аравии предложил схему эксперимента для осуществления бесконтактной телепортации, которую он назвал «контрпортацией». В отличие от квантовой телепортации, контрпортация не требует передачи от отправителя к получателю локального сигнала, но необходимо убедиться в самой возможности передать такой сигнал. Также контрпортация не происходит мгновенно и постулат Эйнштейна о невозможности передачи информации быстрее скорости света не нарушается. В 2017 г. китайские физики впервые установили контрфактическое квантовое соединение, осуществив телепортацию информации без локальной передачи частиц или энергии. Они успешно реализовали схему Салиха, используя квантовый эффект Зенона и однофотонный источник. Используя в качестве носителя информации фазу света, учёные контрфактически передали чёрно-белое растровое изображение из пункта А в пункт Б, не посылая сигнал.

Тем временем Салих, ныне – почётный научный сотрудник лаборатории технологии квантовой инженерии Бристольского университета, занимается моделированием на квантовом компьютере червоточины в пространстве-времени, или моста Эйнштейна-Розена. Это не настоящая червоточина, которая теоретически может соединять две чёрные дыры, но её достаточно для контрфактической передачи состояния между запутанными кубитами, квантовыми процессорами и даже в масштабах квантового интернета. Следующий шаг – отправка через такую червоточину макроскопических объектов или даже компьютера с искусственным интеллектом. Тем самым можно осуществить экспериментальную проверку многомировой интерпретации, предложенную Дэвидом Дойчем ещё в 1985 г., и, по словам Салиха, получить «неопровержимое доказательство существования основной физической реальности».
И снова квантовая запутанность, или как увидеть, не глядя
Напоследок рассмотрим ещё один пример слабого измерения, связанный с квантовой запутанностью и ЭПР-парадоксом. Этот опыт предложил Дэвид Бом для проверки теории скрытых параметров. Предположим, что из одного источника в противоположных направлениях движутся запутанные между собой электрон и позитрон. При измерении относительно одной и той же оси их спины всегда получаются противоположными. Но каждый из наблюдателей сам выбирает, относительно какой оси измерять спин, и получает абсолютно случайный результат (+1/2 или -1/2). Только если один из наблюдателей сообщает свой результат второму, тот может с уверенностью сказать, что спин будет противоположным, ещё не измеряя его (если оба выбрали одну ось). В каком-то смысле это уже бесконтактное измерение. Но что, если они выбрали разные оси измерения?

Например, Алиса измеряла спин относительно вертикальной оси и получила +1/2, а Боб выбрал диагональную проекцию. Результат измерения Боба будет случайным, т.е. положительным или отрицательным с вероятностью 50/50. Но, если до своего измерения он локально получит информацию о результате измерения Алисы, его вероятности перераспределятся. Допустим, если у Алисы спин «вверх», то у Боба он с вероятностью 90% будет «вниз» и с вероятностью 10% — «вверх». А если у Алисы «вниз», то у Боба – 10% «вниз» и 90% «вверх». Проверить эти вероятности можно путём статистического подсчёта результатов многих измерений. Выходит, что получение Бобом информации от Алисы является слабым измерением, в значительной степени определяющим результат второго, «сильного» измерения.
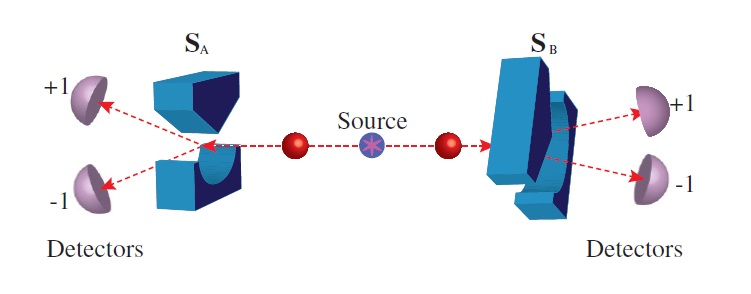
В копенгагенской интерпретации направление спина частицы не является определённым до момента измерения. Волновая функция отражает только знание наблюдателя о квантовой системе – его субъективные вероятности получить тот или иной результат измерения. А коллапс волновой функции рассматривается как перераспределение его субъективных вероятностей, которое не обязательно предполагает, что вероятность какого-то одного результата увеличивается до 100%, а остальных – снижается до 0%. В данном случае при получении Бобом информации от Алисы волновая функция его частицы частично коллапсирует, что соответствует перераспределению его субъективных вероятностей с 50/50 на 90/10 или 10/90. А второй коллапс происходит тогда, когда он проводит «сильное» измерение и получает конкретный результат измерения. Можно подумать, что именно знание Боба о результатах измерений Алисы влияет на статистику его измерений. Но с таким же успехом Боба можно заменить компьютером, который будет автоматически выбирать базис, получать от Алисы информацию и проводить измерение. Конечно, статистику измерений компьютера всё равно будет смотреть человек, который не сможет доказать, что она не появилась в момент его взаимодействия с компьютером. Но это прямой путь к солипсизму, не имеющему никакого отношения к науке и её методам. Подробнее о том, влияет ли наблюдатель на результат эксперимента, я рассказывал в статье «Эффект наблюдателя».
В многомировой интерпретации волновая функция – реальный физический объект, эволюционирующий унитарно согласно уравнению Шрёдингера. Иллюзия случайного коллапса возникает из-за того, что наблюдатель не может предсказать, в какой вселенной он осознает себя в результате измерения. Каждый результат реализуется с вероятностью 100%, а вот где по итогу окажется наблюдатель, зависит от «толщины» ветвей Мультивёрса, соответствующей распределению вероятностей по правилу Борна. В нашем примере Алиса в моменты выбора базиса и своего измерения переходит в суперпозицию своих двойников, запутанных каждый со своей версией вселенной в силу декогеренции. Коллапса волновой функции не происходит, но теперь частица Боба запутана с обеими версиями Алисы и обеими версиями её вселенной. Когда Боб выбирает ось измерения, он тоже расщепляется на столько версий, сколько может быть осей. Затем каждая версия Боба получает информацию о результатах измерения от каждой версии Алисы и проводит своё измерение. Здесь начинается самое интересное.
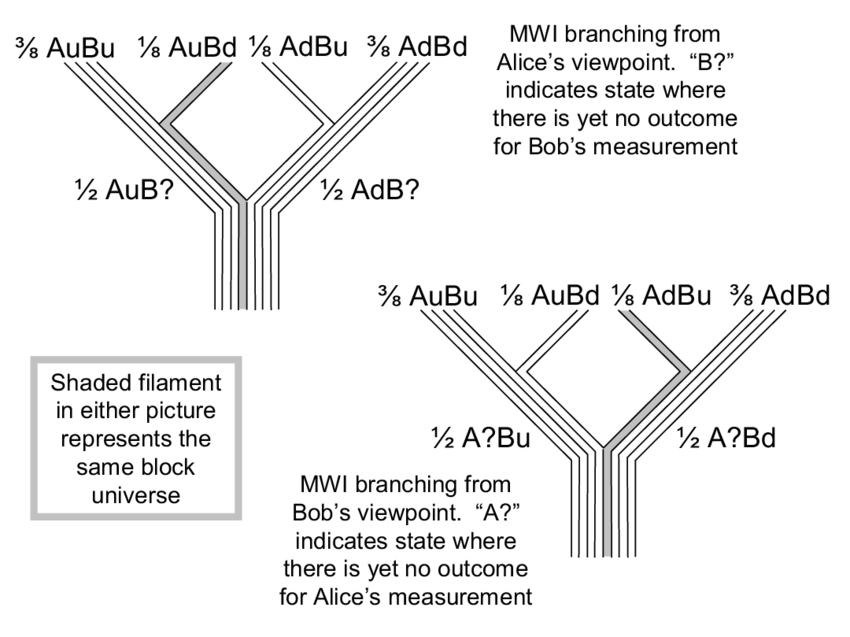
В той ветви, где Алиса выбрала вертикальный базис и измерила верхний спин, а Боб выбрал диагональный базис, версии Боба делятся в соответствующей пропорции: в 90% вселенных Боб измеряет верхний спин, а в 10% вселенных – нижний. Там, где Алиса измерила нижний спин, вселенные делятся в противоположной пропорции. Аналогичное ветвление происходит и с теми вселенными, где Алиса и Боб выбирали другой базис. Но, поскольку не все результаты измерений совместимы (например, при выборе одинакового базиса значения спина у Алисы и Боба не могут совпадать), то не все версии Алисы и Боба смогут встретиться в одной вселенной. Вселенные с противоположными результатами измерения спина интерферируют конструктивно, а вселенные с одинаковыми результатами интерферируют деструктивно и отменяются. Эволюция волновой функции предопределяет, с какой копией Алисы после измерения может встретиться каждая копия Боба, но сами результаты измерения для каждого наблюдателя случайны, пока они их не согласуют.
Если у вас ещё не закипел мозг и вы смогли дочитать статью до этого момента, я вас поздравляю. Не знаю, как вам, но по моему ощущению перечисленные эксперименты расширяют сознание похлеще коанов дзэн-буддизма и апорий Зенона. Об этих квантовых парадоксах мало кто говорит, хотя они не менее важны, чем кот Шрёдингера, эффект наблюдателя или ЭПР-парадокс. Если раньше контрфактические события относились исключительно к сфере воображаемого, то теперь они оказывают реальное влияние на результаты экспериментов. Думаю, это ясно и недвусмысленно свидетельствует о существовании альтернативных историй параллельно с нашей и о необходимости включить их в научную картину мира в рамках многомировой интерпретации квантовой механики или более общей теории конструкторов. Рано или поздно нам придётся признать параллельные миры реально существующими в том же смысле, что и наблюдаемая вселенная. Впервые в своей истории наука экспериментальным путём прикоснулась к невидимому – не к мифическим «тонким мирам», «информационным полям» или «духовным сущностям», а к физически реальным событиям, происходящим не в нашей вселенной.
Сейчас нам трудно даже представить, какими изобретениями обернётся открытие слабых измерений и контрфактических вычислений. Сфера их применимости потенциально бесконечна, как и весь научно-технический прогресс. Думаю, вас, как и меня, удивляет сама возможность «взломать» физику и осуществить подобные вещи. Природа как будто специально оставила эти лазейки в своих законах, чтобы мы ими воспользовались, когда придёт время. Ведь сами по себе во Вселенной не появляются ни интерферометры, ни квантовые компьютеры – их может создать только разум. Кто-то увидит в этом признаки «тонкой настройки» и разумного замысла, кто-то – проявление вычислительной универсальности и фрактального самоподобия Вселенной, а кто-то – свидетельство универсальной эволюции. Я пока оставлю этот вопрос открытым, но буду возвращаться к нему ещё не раз.


