
Одним из самых древних примеров инженерии является дерево. Нет, не растущее в лесу, а переброшенное через ручей для более удобного, быстрого и сухого его пересечения. Именно такими были первые мосты. Позднее они стали сложнее, люди начали использовать камень, а затем и металл. Города росли, торговля развивалась, а реки, озера, ущелья и впадины более не затрудняли перемещения людей. Развитие технологий, в частности транспорта, позволило и даже потребовало строить мосты больше, выше и, естественно, длиннее. Несмотря на то, что машин в современных городах порой больше, чем людей (по крайней мере, так часто кажется, особенно когда стоишь в пробке), пешеходные мосты все же не утратили своей актуальности. Строительство моста требует точных расчетов, в которых будут учтены все возможные факторы, которые в той или иной степени могут повлиять на его стабильность и целостность. Но даже люди, идущие по мосту, могут стать причиной его раскачивания. Ученые из университета штата Джорджии (США) проанализировали мост Миллениум в Лондоне и выяснили, что его нестабильность никак не связана с синхронизацией пешеходов, как это считалось ранее. О какой синхронизации идет речь, и какие на самом деле причины шаткости пешеходных мостов? Ответы на эти вопросы мы найдем в докладе ученых. Пошли. Поехали.
Основа исследования
Мост Миллениум, пересекающий Темзу, является одним из самых знаменитых пешеходных мостов в мире и очень популярная достопримечательность Лондона. Он был открыт, как подсказывает нам название, в 2000 году на стыке тысячелетий. Габариты у него не самые внушительные: 4 метра в ширину и 370 в длину.

Мост Миллениум
Открытие моста было одновременно радостным и печальным днем для его проектировщиков. Во-первых, сама королева Елизавета II присутствовала на церемонии. Во-вторых, желающих прогуляться по новому мосту было много — в первый день по нему прошлись 100000 человек. Эта популярность и выявила недочет моста — он был шатким, как его в последствии и прозвали лондонцы. В попытках понять причину дефекта, инженеры пришли к выводу, что она кроется в резонансе. Попытки ограничить число пешеходов, одновременно пребывающих на мосту, привели к многолюдным очередям. Посему было решено добавить в конструкцию демпферы, что решило проблему, и в 2002 году мост был открыт повторно.
Тем не менее у ученых были вопросы касательно причины раскачивания моста и сомнения в том, что это происходило из-за резонанса.
Для начала стоит затронуть тему синхронизации и резонанса. Ученые объясняют, что синхронизация связанных почти идентичных осцилляторов приводит к возникновению порядка как в естественных, так и в искусственно созданных сложных системах. Одним из лучших объяснений этих явлений считается модель Курамото, примером которой часто выступает именно нестабильность моста Миллениум в день его первого открытия.
Японский физик Ёсики Курамото предложил математическую модель, способную описать синхронизацию. Суть модель в том, что каждый из связанных осцилляторов имеет собственную частоту (ωi), и что каждый связан со всеми другими в равной степени.
Лекция на тему «Модель Курамото и феномен синхронизации».
Однако, многие ученые еще в 2000-ых подвергали сомнению тот факт, что именно модель Курамото может полноценно объяснить причину шаткости моста Миллениум.
В рассматриваемом нами сегодня труде ученые предлагают иной подход, основная суть которого в том, что любая синхронизация расстановки ног пешеходов является следствием, а не причиной нестабильности моста.
Любопытно и то, что спустя 4 дня после открытия моста Миллениум нобелевский лауреат по физике Брайан Дэвид Джозефсон сказал следующее:
Проблема Моста Миллениум имеет мало общего с толпами, идущими шаг в шаг: она связана с тем, что люди делают, пытаясь сохранить равновесие, если поверхность, по которой они идут, начинает двигаться, и аналогична тому, что может произойти, если несколько людей одновременно встают в маленькой лодке. В обоих случаях возможно, что движения, которые люди совершают, пытаясь сохранить равновесие, приводят к усилению любого уже имеющегося покачивания, так что раскачивание продолжает ухудшаться.
Суть данного высказывания в том, что для сохранения равновесия каждый пешеход должен стремиться потерять угловой момент в своей фронтальной плоскости. Кроме того, есть доказательства того, что силы слева и справа не обязательно усредняются. Таким образом, энергия поперечной вибрации передается от пешехода к мосту. Фактически, каждый пешеход применяет к мосту отрицательное демпфирование.
Ранее количественно оценить влияние отрицательного демпфирование было проблематично. Было предложено немало теорий, но все они не давали четкого ответа на вопрос — может ли отрицательное демпфирование быть следствием синхронизации или же синхронизации является следствием отрицательного демпфирования?
В своем исследовании ученые нашли ответ на этот вопрос. Они проанализировали эмпирические данные, разработали новое независимое от модели выражение для среднего отрицательного демпфирующего эффекта и подробно объяснили то, как отрицательное демпфирование в среднем является естественным следствием движения пешеходов.
Немного истории шатких мостов
Первый задокументированный инцидент с пешеходным мостом датируется 12 апреля 1831 года. Тогда Бротонский висячий мост (Англия) обрушился из-за динамической нестабильности, вызванной марширующими войсками. С тех пор бытует мнение, что солдатам следует избегать марша шаг в шаг, если их частота движения может резонировать с естественной (вертикальной) частотой колебаний моста. Порой солдатам даже отдают приказ нарушить строй, чтобы «рассинхронизировать» шаг.
Вертикальные колебания мостов из-за случайного воздействия пешеходов по-прежнему вызывают озабоченность, но до 2000 года крайне мало внимания уделялось боковым колебаниям. Считалось, что при нормальной ходьбе поперечный компонент силы реакции на порядок меньше вертикальной составляющей, и в отсутствие согласованности между пешеходами результирующая реакция моста будет незначительной.
Мост Миллениум был спроектирован в результате сотрудничества инженеров, архитекторов и художников как подвесной мост с очень низким профилем. Одна из особенностей моста в том, что у него нет явно выраженных вертикальных тросов. Необычная геометрия узкого пролета способствовала тому, что мост имел большую гибкость, чем большинство мостов в поперечном направлении, учитывая собственные частоты, аналогичные типичным частотам шагающих пешеходов. При этом его относительно небольшая масса также делала его восприимчивым к вибрациям.
Мост Миллениум в день открытия.
Одним из доказательств связи между раскачиванием моста в день его открытия и синхронизацией является видео (выше), в котором мост больше напоминает большие качели.
Однако, ученые хотят, чтобы мы посмотрели видео внимательнее. Необходимо различать синхронизацию движений головы и верхней части тела (что хорошо видно на видео) и синхронизацию шагов на пролете. Видео, в котором была бы видна синхронизация именно шагов, нет. Ученые говорят, если же посмотреть вышеуказанный ролик еще раз, то видно, что синхронизация шагов отсутствует, так как у людей разная скорость движения. Более того, пешеход, обеспечивающий эффективную отрицательную демпфирующую силу на мост (обязательно на частоте моста) будет демонстрировать компонент движения верхней части тела на этой частоте.

Таблица №1

Таблица №2
На данный момент существует немало мостов, которые, как известно, демонстрируют поперечные колебания из-за движения пешеходов (таблица №1 — есть количественные данные, таблица №2 — нет количественных данных). Но в последнем столбце этих таблиц наблюдаются скудные доказательства синхронизации пешеходов.
География шатких мостов действительно обширна и не имеет каких-либо предпочтений. Явления раскачивания моста ввиду большого числа пешеходов встречались и в Европе, и в Азии, и в Северной Америке и т.д.

Бруклинский мост
Бруклинский мост в 2003 году начал раскачиваться, когда по нему прошла толпа вынужденных пешеходов (было отключение электроэнергии), из-за чего многие начали терять равновесие и испытывать тошноту.

Мост Сквибб-Парк
Из недавних происшествий можно вспомнить деревянный мост Сквибб-Парк (Бруклин, Нью-Йорк, США), на строительство которого ушло почти 4 миллиона долларов. Мост разрабатывался как стабильный и безопасный. Но со временем мост начал колебаться вертикально и горизонтально. В 2017 году его закрыли на ремонт стоимостью 2.5 миллиона. Потом вновь открыли, и он прослужил еще два года, а затем его снесли из-за опасений по поводу его структурной целостности.
Примеры можно продолжать приводить еще очень долго, но суть проблемы шатких мостов от этого не изменится. Посему перейдем непосредственно к первоисточнику этой проблемы.
Теоретическая база
В ходе формирования теоретической базы для своего исследования ученые сформулировали общее выражение для среднего вклада в расшатывание моста силы взаимодействия одного пешехода за один цикл перехода. Ученые установили, что приращение σ можно записать как сумму трех компонентов:
- σ1 — коэффициент зависящей от скорости боковой составляющей силы пешехода, действующей на мост, без учета регулировки времени походки;
- σ2 — коэффициент зависящей от скорости боковой составляющей силы пешехода с учетом регулировки времени походки;
- σ3 — коэффициент зависящей от скорости боковой составляющей силы при учете адаптации к движению вперед.
Элементы σ2 и σ3 зависят от времени шагов пешеходов в ответ на движение моста. Однако во всех симуляциях было обнаружено, что именно σ1 является наиболее важным эффектом при запуске вибраций большой амплитуды.
Этот эффект, возможно, противоречит здравому смыслу, говорят ученые. Так как можно представить, что при отсутствии фазовой синхронизации между мостом и пешеходом поперечная сила ступни на мосту в среднем будет равна нулю. Тем не менее, это не так.

Изображение №1
Иллюстрация выше противопоставляет силу, передаваемую мосту двумя одинаковыми пешеходами, которые, когда одновременно ставят свою опорную ногу на мост, имеют одинаковые и противоположные походки. Когда они ставят ноги, боковая составляющая силы стопы каждого пешехода одинакова и противоположна, поэтому на мосту нет чистой боковой силы.
Предположим, что в определенный момент времени (Δt) мост перемещается влево, так что нога синей фигуры уменьшает свой угол к вертикали во фронтальной плоскости, тогда как угол ноги красной фигуры увеличивается. Таким образом, во время движения моста величина боковой составляющей боковой силы стопы красной фигуры увеличивается, тогда как у синей фигуры уменьшается. Следовательно, в среднем происходит изменение результирующей силы в направлении движения моста.
Выражения для σ1 — σ3 должны оцениваться индивидуально для каждого пешехода (i) и будут зависеть от частоты шага этого пешехода (ωi), а также от частоты (Ω) колебаний моста в рассматриваемом режиме. Таким образом, полный эффективный коэффициент демпфирования (cT) моста с N пешеходами можно выразить так:
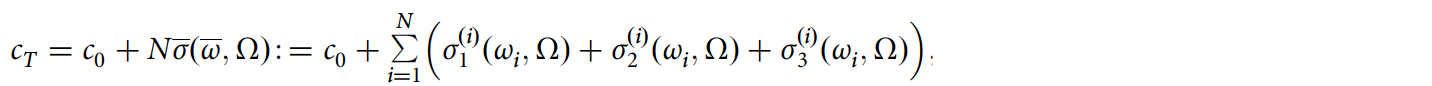
где c0 — коэффициент естественного (пассивного) демпфирования моста; σ(ω, Ω) — средний коэффициент демпфирования на пешехода; ω — средняя частота шагов пешехода.
Было обнаружено, что в большом диапазоне частот пешеходов и мостов в среднем σ < 0. Допустим, что пешеходы добавляются к мостовому пролету один за другим, а затем, когда достигается критическое число (N = Ncrit = — c0 /σ) пешеходов, общее модальное демпфирование (cT) моста станет отрицательным. Отрицательное демпфирование вызовет экспоненциальный рост амплитуды колебаний моста.
Моделирование теории
Чтобы проверить вышеописанную теорию, ученые провели моделирование на трех различных математических моделях, описывающих количество пешеходов в сочетании с боковой модой моста.
В каждом случае учитывалось, что ходьба — это процесс, в котором опорная нога действует как жесткая стойка, заставляя центр массы тела (CoM от centre of mass) действовать как перевернутый маятник во фронтальной плоскости при каждом шаге.

Изображение №2
В ходе моделирования было разработано три варианта модели (схема выше) пешехода. Модель 1 — самая простая, основанная на линеаризации перевернутого маятника во фронтальной плоскости для малых углов. Предполагается, что динамика в сагиттальной плоскости не зависит от бокового положения стопы, а переходы стопы происходят с регулярным интервалом в заданное время. При каждом переходе новое боковое положение стопы регулируется биофизическим законом управления («Control of lateral balance in walking — Experimental findings in normal subjects and aboveknee amputees»), который повышает стабильность во время горизонтального движения.
Модель 2 — это переосмысление модели 1, в которой время постановки стопы изменяется как кинематическое следствие бокового движения моста и положения стопы.
Модель 3 предполагает, что время шага определяется исключительно динамикой во фронтальной плоскости, а переход ног происходит каждый раз, когда CoM пешехода проходит через контрольную позицию, определяемую как нулевое боковое смещение.
Параметры для моделирования были основаны на серии экспериментов, проведенных на мосту Миллениум перед его повторным открытием. Через равные промежутки времени (Tadd) на мост добавлялось по одному пешеходу, пока их число не достигло N = 275. В моделирование было два варианта Tadd: 20 и 10 секунд.
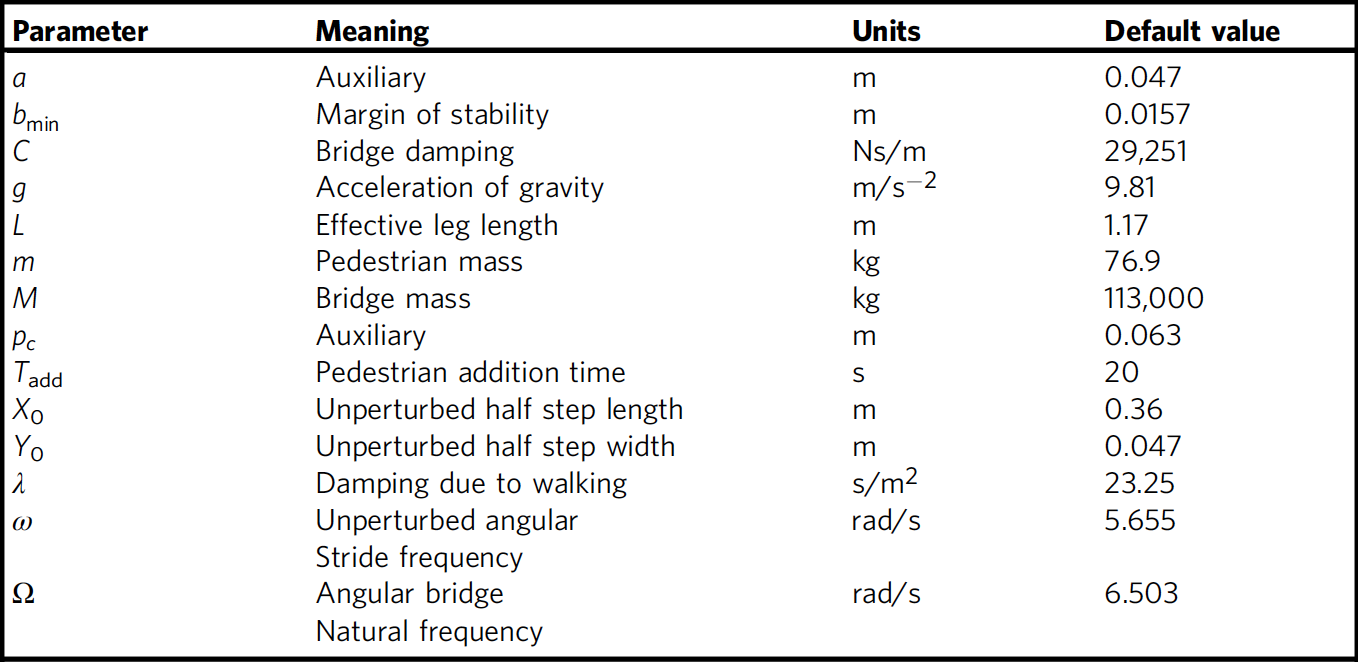
Таблица №3: перечень параметров, использованных в моделировании, и их значения.
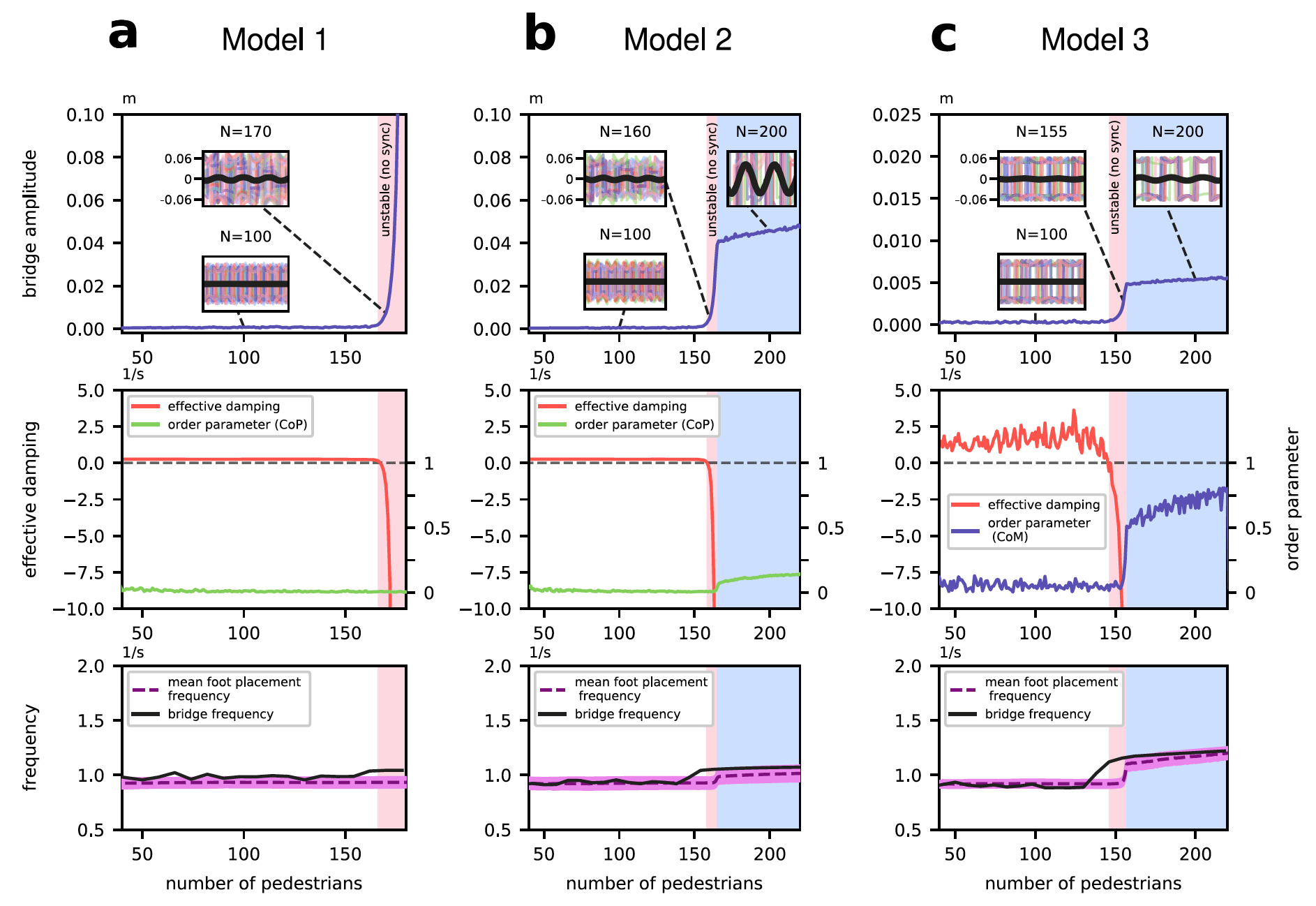
Изображение №3
Выше представлены результаты моделирования с применением всех трех вариантов модели для Tadd = 20 секунд. Для каждой модели численно проверялось выражение для полного эффективного демпфирования (cT; формула выше) путем вычисления σ1(i), σ2(i) и σ3(i) для каждого пешехода (i). Дополнительно вычислялся параметр порядка Курамото (r):

где φi — численно рассчитанная фаза CoM (центр массы) или CoP (от centre of pressure, т.е. центр давления) i-го пешехода; ψ — средняя фаза; ⟨·⟩ — среднее время.
Если r = 1, то имеет место полная синхронность, если же r = 0, то некоррелированное движение.
Моделирование показало, что начало движения моста большой амплитуды совпадает с тем, когда вычисленное cT становится отрицательным при N = Ncrit. Для модели 1, в которой нет регулировки частоты ходьбы, амплитуда колебаний моста неограниченно растет. Но в модели 3 начало движения с умеренной амплитудой запускает процесс повышенной согласованности между движением пешехода и движением моста. Параметр порядка указывает на то, что затем возникает повышенная синхронность между каждым пешеходом и мостом. Затем амплитуда колебаний моста увеличивается.
Модель 2, которая является более реалистичной версией Модели 1 для более высокой амплитуды движения моста, продемонстрировала аналогичное насыщение амплитуды и когерентность после возникновения нестабильности.
Дальнейшее моделирование моделей 2 и 3 для различных частотных параметров показало, что нестабильность находится приблизительно на уровне N = Ncrit. Это приводит к различной степени синхронности по мере роста амплитуды.
Таким образом, критерий отрицательного демпфирования можно понимать как причину нестабильности во всех случаях. Кроме того, разная степень синхронности является следствием, а не причиной нестабильности.
Далее ученые поставили перед собой вопрос — как коэффициент отрицательного демпфирования зависит от моста и средней частоты шага пешехода Ω и ω, и может ли он быть увеличен или подавлен резонансными эффектами?

Изображение №4
Выше представлены результаты многократного моделирования, где показано вычисленное значение σ как функция отношения Ω / ω моста к средней частоте пешехода.
При условии резонанса (желтая точка на 4a), когда ω = Ω, существует теоретическое предсказание наличия большого диапазона значений σ в зависимости от относительной фазы между мостом и пешеходом. Но в ходе моделирования это предсказание не подтвердилось. Модель 2 показала особенности больших отрицательных значений σ чуть ниже Ω/ω = 1 и большие положительные значения чуть выше Ω/ω = 1.
Считается, что это происходит из-за адаптации времени шага в ответ на возмущения от движения моста, что дает аналогичные эффекты, которые ранее были обнаружены численно для перевернутого маятника, идущего по вертикально колеблющейся конструкции.
Ученые также обращают внимание на нехватку данных в определенных областях нижнего графика на 4b и очевидную двухмодальность данных. Это связано с тем, что для модели 3 движение пешеходов с ограниченным циклом является новым свойством модели, а не входным параметром, как для моделей 1 и 2.
Для всех трех моделей было обнаружено, что среднее значение σ в основном зависит от соотношения частот, будучи лишь слабой функцией отдельно частоты пешехода или частоты моста.
Для всех моделей также было установлено, что Ncrit минимизируется не тогда, когда существует совпадение частот между частотами пешехода и моста (Ω/ω = 1), но когда частота пешеходов меньше частоты моста, Ω/ω ≈ 1.3 для моделей 1 и 2 и Ω/ω ≈ 1.1 для модели 3.
Следовательно, отрицательное демпфирование может наблюдаться на любой частоте в рассматриваемом диапазоне частотных соотношений. Но есть и некоторое отношение частот, для которых σ положительно. Если пешеходы ходят на этих частотах, их движение повысит устойчивость моды моста, а не уменьшит ее.
По словам ученых, объяснение этой частотной зависимости можно резюмировать как вопрос времени. Описание изображения №1 неявно предполагает, что мост движется в одном направлении во время каждого шага, а частоты моста и пешехода одинаковы. Особые настройки этого отношения частот могут привести к обратному эффекту. Тем не менее, в рассматриваемом диапазоне частот как размер областей отрицательного демпфирования, вызванного пешеходами, так и его среднее значение, значительно превышают размер положительного демпфирования.
На изображении №1 также показано, как движение моста нарушает симметрию нагрузки, прикладываемой пешеходами, так что долгосрочные средние значения необязательно равны нулю. Это только часть объяснения, поскольку оно не учитывает движение центров масс пешеходов и различные стратегии размещения стопы, которые могут быть приняты для поддержания равновесия.
В принципе, положение стопы зависит от боковой скорости центра масс пешехода. Однако остается неопределенность в отношении того, следует ли определять скорость относительно качающегося моста (относительная скорость) или стационарной точки, относительно которой движется мост (абсолютная скорость).
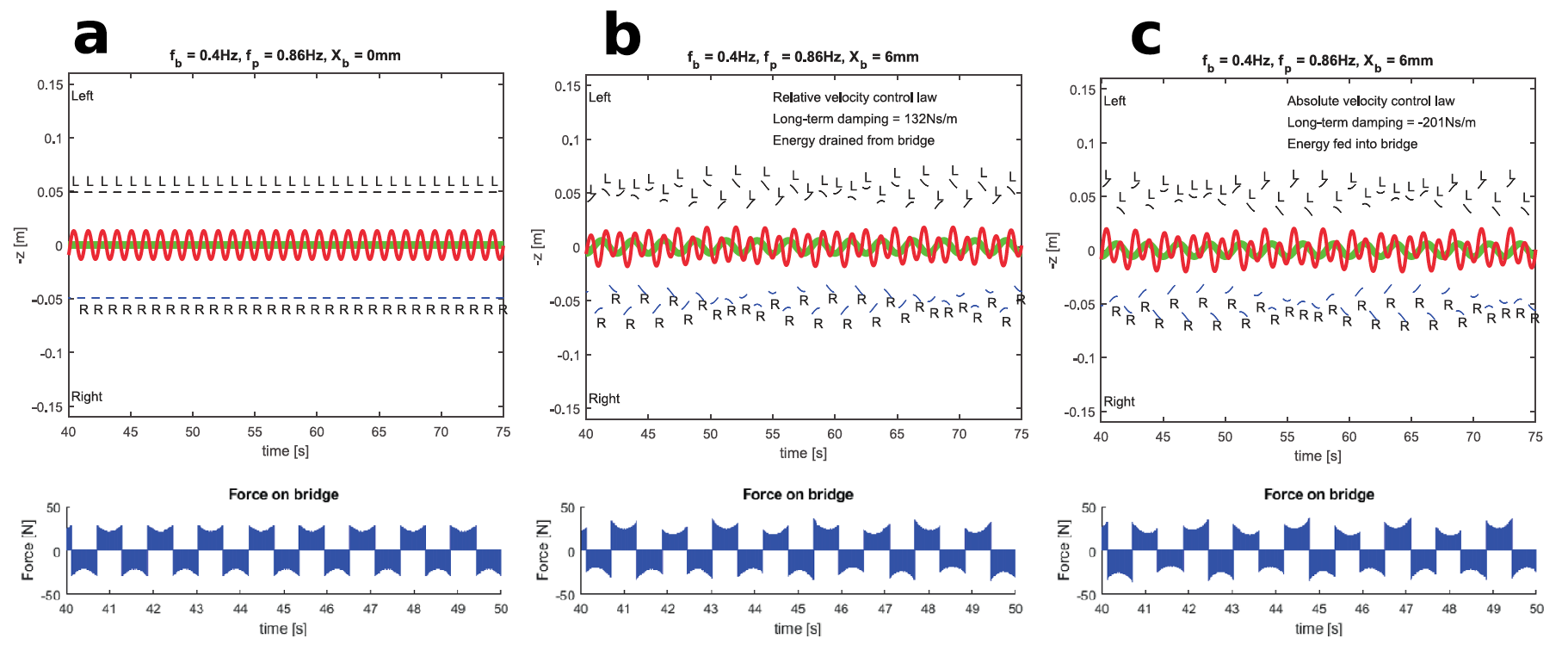
Изображение №5
Выше представлены результаты модели 1, а также соответствующие силы, приложенные к мосту в этих случаях. Поскольку движения моста малы, силы во всех вариантах будут равны.
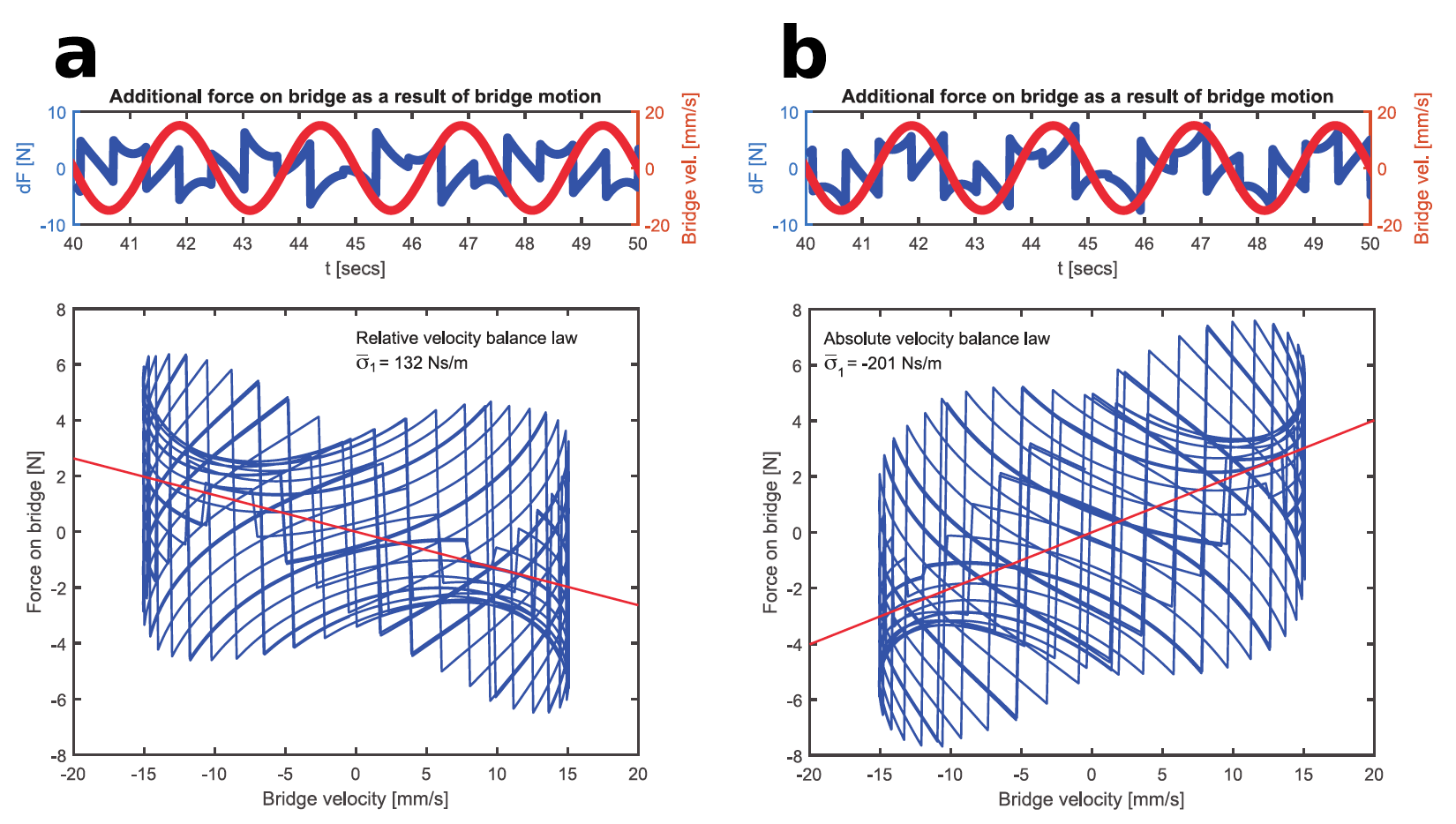
Изображение №6
Конечно, изменение приложенных сил, возникающее в результате движения моста, может наблюдаться, но оно будет незначительным (изображение №6).
Пешеходы создают силы, которые отрицательно коррелируют со скоростью моста, что приводит к положительному демпфирующему эффекту. Напротив, дополнительные силы, создаваемые пешеходом, реализующим закон абсолютного баланса скоростей, положительно коррелируют со скоростью моста, что приводит к отрицательному демпфирующему эффекту, который передает энергию мосту.
Таким образом, движения моста заставляют пешеходов корректировать положение своих ног, что вызывает небольшие квазипериодические силы, составляющие частоту моста. В зависимости от принятого закона баланса (и частоты движения моста и других параметров) фазы этих дополнительных сил могут либо передавать на мост, либо извлекать ее.
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.
Эпилог
В рассмотренном нами сегодня труде ученые объясняют связь между пешеходами и шаткими мостами. Ярким примером неустойчивости конструкции является мост Миллениум, который и стал основой исследования. В 2017 году было опубликовано исследование, показавшее, что мост оставался стабильным, пока по нему шло 164 человека. Но стоило добавить еще одного пешехода, и мост начинал изображать из себя качели. Это открытие вызвало интерес у авторов рассмотренного нами труда. Оно показывало, что суть проблемы может быть далека от синхронизации Курамото, которую считали причиной расшатывания пешеходных мостов.
Используя данные эмпирических экспериментов и математическое моделирование, ученые пришли к занимательному выводу: не люди раскачиваются из-за шаткого моста, а мост раскачивается из-за шатких людей. Представьте себе деревянную лодку посреди океана, в которой туда-сюда ходят люди. Из-за волн, лодка раскачивается, а люди в попытках сохранить равновесие и не упасть за борт меняют стратегию движения. Таким образом они влияют и на саму лодку через механизм отрицательного демпфирования.
Говоря о мостах, пример с лодкой можно перефразировать — движение пешеходов влияет на мост и увеличивает его колебание. Другими словами, синхронизация колебаний пешеходов и моста хоть и может привести к его раскачиванию, но в подавляющем большинстве случаев причина не в этом, а в том, что люди просто перестраивают свою походку, чтобы не упасть.
Данное исследование и его результаты могут стать отличным инструментом для инженеров в проектировании будущих мостов, так как теперь они могут учитывать эффекты отрицательного демпфирования. Сами же ученые намерены продолжить свой труд, уделив внимание тому, как на стабильность мостов могут влиять взаимодействия между людьми, идущими по нему, а также влиянию толпы. Есть и более амбициозная идея — создать устройство, которое будет собирать энергию моста и питать датчики, которые будут отслеживать целостность его конструкции.
Благодарю за внимание, оставайтесь любопытствующими и хорошей рабочей недели, ребята. 🙂
Немного рекламы
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Maincubes Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?


