Предыстория
Очень давно не брал в руки шашек и почти ничего не писал на хабре. В основном активность в последние годы здесь ограничивается простановкой плюсов и минусов под статьями и комментариями. Поэтому коротко о себе. По образу жизни и работы я — физик‑теоретик, доцент кафедры теоретической же физики в Пермском классическом университете, и немного эфирно‑паяльный радиолюбитель. Поскольку физик‑теоретик — понятие очень абстрактное, размытое и растяжимое, заниматься по научной тематике доводилось различными задачами. Гидродинамика, нелинейные процессы, спектральный и вейвлет‑анализ, немного биомедицинских работ. Это всё немного пылится в прошлом, а сейчас основной темой стали спиновая динамика и всяческие волны намагниченности в твёрдых телах.
Давняя история магнетизма, ЯМР/ЭПР и спиновой динамики у нас здесь богатая (современность вот, увы, не очень). О ней напоминают, в частности, сборники «Радиоспектроскопия», выходившие в университете чуть реже, чем раз в год, начиная с 1962. И вот, при пролистывании одного из этих сборников, а именно за 1976 год, попалась на глаза статья наших уважаемых профессоров — Евгения Карловича Хеннера и его наставника, Ивана Григорьевича Шапошникова, — с неярким, но ёмким названием «Об одном численном методе статистической теории магнитного резонанса в твердых телах». Казалось бы, обычная заметка на 8 страниц об идее и особенностях реализации и тестирования расчётного метода. Но почти половину её объёма составил полный листинг для одной из реализаций языка АЛГОЛ-60, который в Перми, скорее всего, крутился на М-220 в нашем вычислительном центре (да простят меня мехматовцы, если в эту строку вкралась фактическая ошибка). Как это выглядит на бумаге, показано на фотографии. Для экономии места ликвидировано всё возможное форматирование, но, хвала точкам с запятыми и коротким комментариям, код вполне читаем и более‑менее структурирован.

Немножко квантовой магии
Коротко, что же этот «один численный метод» делает. Иван Григорьевич в 1994 г. собственноручно составил список из ста, на тот момент, начиная с 1936 г., своих публикаций, к каждой из которых дал краткую и ёмкую аннотацию. Оригинал списка хранится у нас на кафедре среди других артефактов. Да, было время, когда не количеством публикаций и цитируемостью мерялись учёные. Конкретно к описываемой здесь статье аннотация такова:
С целью изучения некоторых вопросов магнитного резонанса в магниторазведённых кристаллах, предложен и использован численный метод точного учёта многочастичных взаимодействий (без привлечения теории возмущений) между близко расположенными магнитными ионами, дополненный статистическим усреднением по случайной выборке из полной совокупности возможных для данной концентрации распределений магнитных ионов по решётке..
Что ж, давайте пройдёмся по пунктам.
Моделирование магнитного резонанса в магниторазведëнном кристалле. Или, как принято говорить в современных текстах, в магниторазбавленном. Это обширный пласт материалов, хотя в большинстве статей упоминается только арсенид галлия, допированный марганцем, Mnx: Ga(1-x) As, где доля Mn x — процентов 5–8. Это вроде и полупроводник, но очень хорошо чувствующий магнитное поле. Именно это и интересно. Или, прости господи, графен с сидящими на нём атомами чего‑то более магнитного, чем углерод. Тут получается примерно то же самое, что и с арсенидом галлия, с поправкой на необычное поведение электронов.
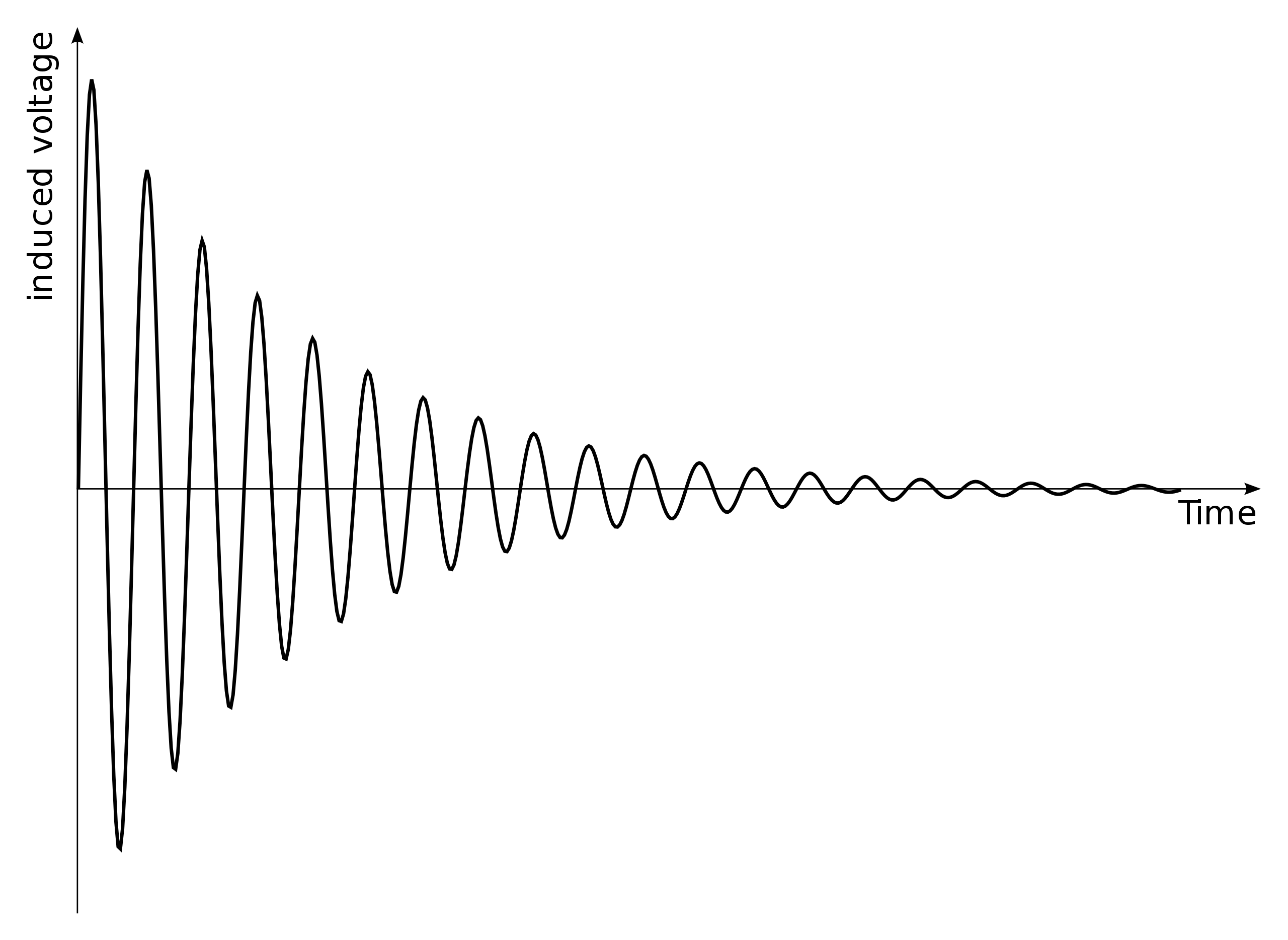
Как нам залезть в этот материал и узнать его структуру и энергетический спектр? Много способов. Один из них — это магнитный резонанс. Помещаем образец в сильное постоянное поле, и каждый магнитный центр начинает крутиться со своей собственной частотой, определяемой его окружением. «Стукаем» импульсом перпендикулярного поля или их серией, магнитные моменты частично «падают набок» и начинают возвращаться к исходной прецессии. Тут‑то мы их и ловим — записывается сигнал намагниченности во времени, откуда находится спектр магнитного резонанса и сопутствующие характеристики. Выглядят они примерно как на картинке. Вообще, спектр можно и напрямую измерить, просто плавно меняя параметры полей и регистрируя поглощение энергии образцом. Исторически это был первый метод, но он, как минимум, менее точный и более долгий.
И всё бы ничего, и даже теорию возмущений для свойств материала можно написать, но случайное распределение магнитных центров — в данном случае примеси марганца — всё портит. Где‑то его много, где‑то поменьше получилось при синтезе, а от окружения плывёт и спектр энергии, и возможные состояния. Вместо упорядоченной структуры у нас месиво кластеров из 2, 3, 4… и т. д. магнитных центров, и все кластеры имеют случайный размер и форму. В результате уровни энергии всего кристалла размазаны в почти что энергетические зоны, а резонансы совершенно не острые. Именно эти данные и генерирует алгоритм, моделируя спектр сигнала от разбавленного материала.
Как это происходит? Создаётся случайный кластер атомов, рассчитываются его свойства, записываются. Затем ещё кластер, ещё, ещё и пока не наберётся приемлемая статистика, и наконец вычисляется осреднëнный спектр магнитного резонанса образца, составленного из этих самых кластеров в предположении, что друг друга они не замечают. Для низких концентраций примеси это отлично работает. Весь расчёт выполняется из первых принципов — честно строится оператор (матрица) гамильтониана, итерационно, методом вращений, вычисляются её собственные значения — уровни энергии кластера, и вероятности переходов между ними под действием поперечного поля. Это весьма ресурсозатратно — если частицы имеют спин 1/2, и кластер содержит N частиц, то приходится строить и диагонализовать матрицу размерами 2N×2N, которая вдобавок ещё и не сильно разрежена. Но в результате программа отрабатывает крайне быстро, 100 случайных конфигураций с 8 частицами от силы за полминуты.
От древнего языка… к древнему языку
Шёл август 2018 года. Время было тихое. Очередная заявка на грант была подана и ждала подведения итогов, статья в ЖЭТФ принята, учебный год ещё не начался, отпуск не закончился, а другие глобальные задачи не очень-то клеились. Чем ещё заниматься учёному-преподавателю при таком раскладе, если не пить? Мгновенно возникло настойчивое желание вдохнуть жизнь в код, напечатанный на тот момент 42 (о, эта магия чисел) года назад. И программа медленно, оператор за оператором, начала воплощаться в окне Visual Studio.
Наверное, спросите, на каком же языке. Яблоко от яблони недалеко падает, а яблоня от яблока — тем более. На тот момент я уверенно работал только с FORTRAN-90, которому у нас долгое время учили на курсе численных методов, и, чего греха таить, научили! Игорь Геннадьевич Семакин гонял всех нещадно, особенно доставалось как раз теоретикам. Думаю, что не зря.
Программа в целом, в том числе в обозначениях переменных, соответствует оригиналу. Немного использованы встроенные средства работы с массивами вместо явного прописывания поэлементной обработки. Вообще, в оригинале весь код написан без особых изысков, практически в лоб, в отличие от нынешних рекомендаций/традиций/правил/стандартов (нужное подчеркнуть). Все переменные — глобальные, и все те несколько процедур, что написаны вместо блоков с метками, не имеют формальных параметров. В исходнике, напомню, их нет, а вместо подпрограмм — вынесенные блоки кода под метками, переход на которые происходит по goto, но по выполнению условия. Эдакий условно‑безусловный переход.
Ну и здесь интенсивно задействована динамическая память — в оригинале предполагалось, что массивы статичны, а их размеры и количество (при вычислении произведения Кронекера) меняются по необходимости прямо в коде (т.е. на перфокартах). Здесь же в процедуре p34 видно, как динамические массивы постоянно стираются и выделяются заново — это происходит формирование полного размера нужных матриц.
Вот оно, что получилось — под спойлером.
.f90
program NMR_rarefied
implicit none
real(8), dimension(:,:,:), allocatable :: dip, a1 ! dipolar interaction and additional
real(8), dimension(:,:), allocatable :: sx, sy, sz, sI, sp, sm, o, u, v, w, & ! spin matrices and additional
x, y, z, r, & ! r = {x, y, z}, distances between magnetic ions (MI)
J0, & ! exchange interactions
ReH, ImH, b, q, q2, & ! Hamiltonian parts and additional
d0, d1 ! for Kronecker product procedure
real(8), dimension(:), allocatable :: x1, y1, z1, & ! coordinates of MI
RT2, RT3, RT4, RT1, sum_sqr, & ! for rotation method
histp, hist ! partial and averaged histogram
logical, dimension(:), allocatable :: mask1
real(8), dimension(1:3) :: e1, e2, e3, d ! lattice basis
real(8), dimension(1) :: i11, k11
real(8) S, eps, & ! spin, precision
alpha, beta, pd, & ! parameters of exchange (A*exp(-B*r)) and dipolar interaction (pd = (hbar*gamma)^2)
res, & ! histogram resolution
s1, s2, c1, c2, & ! rotation parameters
m, e, c
integer N, N1, N2, N3, NN, Nres, & ! total number of MI and their concentration
i, j, k, i1, j1, k1, t, m3, ms, l, r1, ires, & ! counters
f, fn, & ! 2S+1, (2S+1)^N
nh ! number of histogram bars
logical noconv
!----------------------------------------------------
! read and set the initial parameters
!----------------------------------------------------
open(1, file="init.txt", form="formatted", action="read")
read(1,*) eps, S, N, N1, N2, N3, nh, alpha, beta, pd, &
e1, e2, e3, res, Nres
close(1)
f = 2*S + 1; fn = f**N
call RANDOM_SEED()
!----------------------------------------------------
! memory alloc
!----------------------------------------------------
allocate(sx(1:f,1:f)); allocate(sy(1:f,1:f)); allocate(sz(1:f,1:f))
allocate(sI(1:f,1:f)); allocate(sp(1:f,1:f)); allocate(sm(1:f,1:f))
allocate(o(1:f,1:f)); allocate(v(1:f,1:f)); allocate(w(1:f,1:f))
allocate(dip(1:6,1:N,1:N)); allocate(J0(1:N,1:N)); allocate(u(1:N,1:N))
allocate(x(1:N,1:N)); allocate(y(1:N,1:N)); allocate(z(1:N,1:N))
allocate(r(1:N,1:N))
allocate(x1(1:N)); allocate(y1(1:N)); allocate(z1(1:N))
allocate(ReH(1:fn,1:fn)); allocate(ImH(1:fn,1:fn))
allocate(b(1:fn,1:fn)); allocate(q(1:fn,1:fn)); allocate(q2(1:fn,1:fn))
allocate(mask1(1:fn))
allocate(a1(1:N,1:f,1:f))
allocate(RT1(1:fn)); allocate(RT2(1:fn))
allocate(RT3(1:fn)); allocate(RT4(1:fn))
allocate(sum_sqr(1:fn))
allocate(histp(1:nh)); allocate(hist(1:nh))
hist = 0.0d0
open(1, file="MI_coords.txt", form="formatted", action="write")
open(2,file="E.txt", form="formatted", action="write")
!----------------------------------------------------
! spin matrices initialization
!----------------------------------------------------
sx = 0.0d0; sy = 0.0d0; sz = 0.0d0; sp = 0.0d0; sm = 0.0d0; sI = 0.0d0
do i = 1, f, 1
sI(i,i) = 1.0d0
sz(i,i) = S - (i-1)
if(i <= f-1) sp(i,i+1) = dsqrt(dabs(S*(S+1.0d0) - real(i*(i+1))))
enddo
sm = transpose(sp)
sx = 0.5d0*(sp + sm)
sy = 0.5d0*(sm - sp)
!----------------------------------------------------
ires = 1
REALIZATION: do while(ires <= Nres)
!----------------------------------------------------
! generation of MI distribution in lattice
!----------------------------------------------------
x = 0.0d0; y = 0.0d0; z = 0.0d0; r = 0.0d0
COORDS: do
! MI coordinates
do i = 1, N, 1
call RANDOM_NUMBER(d)
d(1) = floor(d(1)*N1); d(2) = floor(d(2)*N2); d(3) = floor(d(3)*N3)
x1(i) = d(1)*e1(1) + d(2)*e2(1) + d(3)*e3(1)
y1(i) = d(1)*e1(2) + d(2)*e2(2) + d(3)*e3(2)
z1(i) = d(1)*e1(3) + d(2)*e2(3) + d(3)*e3(3)
enddo
! MI distances
do i = 1, N, 1
do j = 1, N, 1
if(i /= j)then
x(i,j) = x1(i) - x1(j)
y(i,j) = y1(i) - y1(j)
z(i,j) = z1(i) - z1(j)
! full interaction
r(i,j) = dsqrt( x(i,j)**2 + y(i,j)**2 + z(i,j)**2 )
endif
enddo
r(i,i) = 1.0d0
enddo
if(minval(r) > 0.5d0)exit
enddo COORDS
! write MI coordinated
write(1,'(A,I8)') "Realization ", ires
do i = 1, N, 1
write(1,'(I6, 3E20.6E3)') i, x1(i), y1(i), z1(i)
enddo
write(1,*)
!----------------------------------------------------
! pair interaction evaluation
!----------------------------------------------------
! isotropic part
J0 = alpha*dexp(-beta*r)
dip(1,:,:) = J0 + pd * (1.0d0 - 3.0d0*x**2 / r**2) / r**3
dip(2,:,:) = J0 + pd * (1.0d0 - 3.0d0*y**2 / r**2) / r**3
dip(3,:,:) = J0 + pd * (1.0d0 - 3.0d0*z**2 / r**2) / r**3
! anisotropic part
dip(4,:,:) = -3.0d0*pd*x*y / r**5
dip(5,:,:) = -3.0d0*pd*x*z / r**5
dip(6,:,:) = -3.0d0*pd*y*z / r**5
!----------------------------------------------------
! real part of the Hamiltonian matrix
!----------------------------------------------------
o = sz; call p78()
ReH = b
u = dip(1,:,:); v = sx; w = sx; call p56()
u = dip(2,:,:); v = sy; w = -sy; call p56()
u = dip(3,:,:); v = sz; w = sz; call p56()
u = dip(5,:,:); v = sx; w = sz; call p56()
q = ReH; ReH = 0.0d0
!----------------------------------------------------
! imaginary part of the Hamiltonian matrix
!----------------------------------------------------
u = dip(4,:,:); v = sx; w = sy; call p56()
u = dip(6,:,:); v = sy; w = sz; call p56()
ImH = ReH; ReH = q
!----------------------------------------------------
! Diagonalization of the Hamiltonian matrix
!----------------------------------------------------
t = 0; q = 0.0d0; q2 = 0.0d0
do i = 1, fn, 1
q(i,i) = 1.0d0
enddo
! sum of squares by strings
sum_sqr = 0.0d0
do i = 1, fn, 1
do j = 1, fn, 1
if(i /= j) sum_sqr(i) = sum_sqr(i) + (ReH(i,j)**2 + ImH(i,j)**2)
enddo
enddo
noconv = .false.
! rotation iterations
ROTATION: do
i11 = maxloc(sum_sqr); i1 = i11(1)
mask1 = .true.; mask1(i1) = .false.
k11 = maxloc(ReH(i1,:)**2 + ImH(i1,:)**2, mask=mask1); k1 = k11(1)
m = maxval(ReH(i1,:)**2 + ImH(i1,:)**2, mask=mask1)
if(m < eps)exit
if(t == 100000)then
noconv = .true.
exit
endif
mask1(k1) = .false.
sum_sqr = sum_sqr - sum(ReH(:,i1)**2 + ImH(:,i1)**2, mask=mask1)
i = i1; k = k1
! rotation parameters
e = dabs(ReH(i,i) - ReH(k,k)) / dsqrt( (ReH(i,i) - ReH(k,k))**2 + 4.0d0*(ReH(i,k)**2 + ImH(i,k)**2) )
s1 = dsqrt( 0.5d0*(1.0d0 - e) ); c1 = dsqrt( 0.5d0*(1.0d0 + e) )
if(ReH(i,i) /= ReH(k,k)) s1 = sign(s1, ReH(i,i) - ReH(k,k))
if(ReH(i,k) /= 0.0d0) s1 = sign(s1, ReH(i,k))
s2 = ImH(i,k) / dsqrt(ReH(i,k)**2 + ImH(i,k)**2)
if(ReH(i,k) /= 0.0d0) s2 = sign(s2, ReH(i,k))
c2 = s1 * dabs(ReH(i,k)) / dsqrt(ReH(i,k)**2 + ImH(i,k)**2)
s1 = s1*s2
! make the rotations
RT1 = c1*q(:,i) + c2*q(:,k) + s1*q2(:,k)
RT2 = -c2*q(:,i) + c1*q(:,k) + s1*q2(:,i)
RT3 = -s1*q(:,k) + c1*q2(:,i) + c2*q2(:,k)
RT4 = -s1*q(:,i) - c2*q2(:,i) + c1*q2(:,k)
q(:,i) = RT1; q(:,k) = RT2; q2(:,i) = RT3; q2(:,k) = RT4
RT1 = c1*ReH(:,i) + c2*ReH(:,k) + s1*ImH(:,k)
RT2 = -c2*ReH(:,i) + c1*ReH(:,k) + s1*ImH(:,i)
RT3 = -s1*ReH(:,k) + c1*ImH(:,i) + c2*ImH(:,k)
RT4 = -s1*ReH(:,i) - c2*ImH(:,i) + c1*ImH(:,k)
ReH(:,i) = RT1; ReH(:,k) = RT2; ImH(:,i) = RT3; ImH(:,k) = RT4
RT1 = c1*ReH(i,:) + c2*ReH(k,:) - s1*ImH(k,:)
RT2 = -c2*ReH(i,:) + c1*ReH(k,:) - s1*ImH(i,:)
RT3 = c1*ImH(i,:) + c2*ImH(k,:) + s1*ReH(k,:)
RT4 = -c2*ImH(i,:) + c1*ImH(k,:) + s1*ReH(i,:)
ReH(i,:) = RT1; ReH(k,:) = RT2; ImH(i,:) = RT3; ImH(k,:) = RT4
t = t+1
mask1 = .true.; mask1(i1) = .false.; mask1(k1) = .false.
sum_sqr = sum_sqr + sum(ReH(:,i1)**2 + ImH(:,i1)**2, mask = mask1) &
+ sum(ReH(:,k1)**2 + ImH(:,k1)**2, mask = mask1)
mask1 = .true.; mask1(i1) = .false.
sum_sqr(i1) = sum(ReH(i1,:)**2 + ImH(i1,:)**2, mask = mask1)
mask1 = .true.; mask1(k1) = .false.
sum_sqr(k1) = sum(ReH(k1,:)**2 + ImH(k1,:)**2, mask = mask1)
enddo ROTATION
!----------------------------------------------------
if(noconv)then
print *, "Realization does not converge"
else
print *,ires, ", Rotation finished at ", t, " iterations"
!----------------------------------------------------
! eigenvalues
!----------------------------------------------------
do i = 1, fn, 1
RT1(i) = ReH(i,i)
enddo
! write energy
write(2,'(A,I8)') "Realization ", ires
do i = 1, fn, 1
write(2,'(I6,E20.6E3)') i, RT1(i)
enddo
write(2,*)
!----------------------------------------------------
! evaluate probabilities and histogram amplitudes
!----------------------------------------------------
histp = 0.0d0
o = sx
call p78()
ReH = matmul(b, q); ImH = matmul(b, q2)
d1 = transpose(q); b = transpose(q2)
q = matmul(d1, ReH) + matmul(b, ImH)
q2 = matmul(d1, ImH) - matmul(b, ReH)
do i = 1, fn, 1
do j = 1, fn, 1
c = q(i,j)**2 + q2(i,j)**2
k = floor(1.0d0 + dabs(RT1(i) - RT1(j)) / res)
if(k <= nh) histp(k) = histp(k) + c
enddo
enddo
hist = hist + histp
ires = ires + 1
endif
enddo REALIZATION
!----------------------------------------------------
open(3,file="hist.txt", form="formatted", action="write")
do i = 1, nh, 1
write(3,'(2E20.6E3)') i*res, hist(i) / Nres
enddo
close(1); close(2); close(3)
print *,"Histogram is written at hist.txt"
!----------------------------------------------------
! memory clear
!----------------------------------------------------
deallocate(sx); deallocate(sy); deallocate(sz); deallocate(sI)
deallocate(o); deallocate(v); deallocate(w)
deallocate(ReH); deallocate(ImH); deallocate(b); deallocate(q); deallocate(q2)
deallocate(mask1); deallocate(a1)
deallocate(RT1); deallocate(RT2); deallocate(RT3); deallocate(RT4); deallocate(sum_sqr)
deallocate(histp); deallocate(hist)
deallocate(dip); deallocate(J0); deallocate(sp); deallocate(sm)
deallocate(x1); deallocate(y1); deallocate(z1)
deallocate(x); deallocate(y); deallocate(z); deallocate(r); deallocate(d1)
contains
!----------------------------------------------------
! Kronecker product of one spin and N-1 identity
!----------------------------------------------------
subroutine p78()
b = 0.0d0
do k = 1, N, 1
a1(k,:,:) = sI
enddo
do k = 1, N, 1
a1(k,:,:) = o
call p34()
a1(k,:,:) = sI
b = b + d1
enddo
end subroutine p78
!----------------------------------------------------
! Kronecker product of two spin and N-2 identity
!----------------------------------------------------
subroutine p56()
do k = 1, N, 1
do t = 1, N, 1
if(k /= t)then
a1(k,:,:) = v; a1(t,:,:) = w
endif
call p34()
a1(k,:,:) = sI; a1(t,:,:) = sI
ReH = ReH + u(k,t)*d1
enddo
enddo
end subroutine p56
!----------------------------------------------------
! Kronecker product of N matrices
!----------------------------------------------------
subroutine p34()
if(allocated(d0)) deallocate(d0)
if(allocated(d1)) deallocate(d1)
allocate(d0(1:f,1:f)); d0 = 0.0d0
allocate(d1(1:f**2,1:f**2)); d1 = 0.0d0
d0 = a1(1,:,:)
do m3 = 2, N, 1
NN = f**(m3-1)
do i = 1, NN, 1
do j = 1, NN, 1
do ms = 1, f, 1
do l = 1, f, 1
r1 = (i-1)*f + ms; i1 = (j-1)*f + l
d1(r1,i1) = d0(i,j)*a1(m3,ms,l)
enddo
enddo
enddo
enddo
if(m3 < N)then
deallocate(d0); allocate(d0(1:f**m3,1:f**m3)); d0 = 0.0d0
d0 = d1
deallocate(d1); allocate(d1(1:f**(m3+1),1:f**(m3+1))); d1 = 0.0d0
endif
enddo
deallocate(d0)
end subroutine p34
end program NMR_rarefiedПростите, без подсветки, хабраредактор всё-таки современен
Пройдёт ещё лет десять, и уже этот фортрановский файл можно будет тоже записывать в археологию. А может, уже пора. Но тем не менее, компилируем, запускаем:
И строим из выведенной таблички вполне приличный модельный спектр:
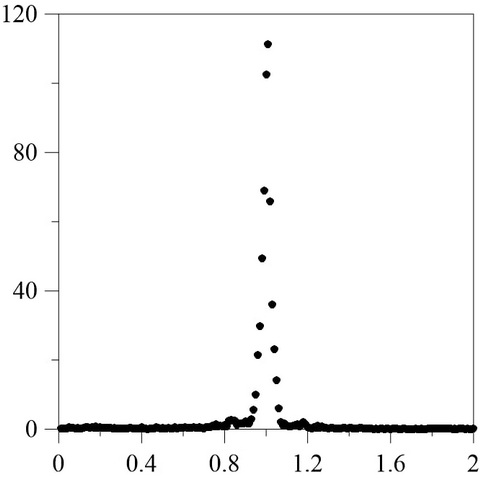
Итоги
Не надо конечно думать, что эта именно программа активно используется. Хотя и правда, мы поразбирались с её результатами и попытались адаптировать для конкретных задач, не без помощи вышеупомянутого автора Е.К. Хеннера. Программа жива, работоспособна и действительно позволяет симулировать магниторезонансные эксперименты. А размер моделируемого кластера частиц на каждой случайной реализации упирается только в объём доступной для размещения массивов памяти.
Для массовых рабочих станций, которыми мы сегодня у себя пользуемся, при 16 Гб RAM это где‑то в районе 12–14 частиц со спином 1/2, в зависимости от загрузки системы другими процессами. Немного, но если накопить статистику по реализациям, получается вполне достоверно. Таких работ относительно немного, но наша группа не одна на этом поприще, к счастью, есть с кем сравниваться в плане разработки и реализации методов. Есть, конечно, подходы и пакеты куда более серьёзные. Например, несравненный Spinach, на котором можно замоделировать, похоже, вообще всё что угодно, вплоть до полноразмерных белковых структур. Если, конечно, есть под рукой суперкомпьютер с GPU — гильбертово пространство квантовой системы от выбора алгоритма моделирования меньше не становится.
Сегодня этот же, по сути, метод частично живёт в виде кода на Python с NumPy и LAPACK, и потихоньку плодит с нашей помощью статьи и дипломы студентов. Чуть более гибко, чуть более просто писать, не думая о внутренней сущности отдельных команд и просто зная, что раз написано, например,np.kron— значит это точно отлаженное и надёжное кронекеровское перемножение матриц, а огромный кусок с методом вращений заменён на единственную строку с вызовомnp.linalg.eigh. По скорости же обе программы, если в Python сейчас оставить только функционал, соответствующий старому исходнику на АЛГОЛ, оказываются абсолютно сопоставимы.
А вот оживить программу, написанную полвека назад и сохранившуюся на пожелтевших страницах — по‑моему, это просто красиво!
Литература
Хеннер Е. К., Шапошников И. Г. Об одном численном методе статистической теории магнитного резонанса в твёрдых телах // Сб. Радиоспектроскопия – ПГУ, Пермь, 1976. – № 10. – С. 74–81.


