А ваш фильтр Калмана правильно работает?

Фильтр Калмана является одним из самых популярных алгоритмов фильтрации. Он широко распространен в машинном обучении, навигационных системах, автопилотируемых устройствах и пр.

В открытых источниках можно встретить множество работ, статей и книг по тому, как работает этот загадочный фильтр, будь то линейный, расширенный (extended), сигма-точечный (unscented) или любой другой фильтр Калмана. Однако, вопрос корректности работы фильтра освещается намного реже.

В это же время фильтр Калмана применяется в системах с особыми требованиями к функциональной безопасности, отказ или неисправность которых может привести, в том числе, к летальным исходам, как это имеет место в случае автопилотируемых устройств. Таким образом, валидация результатов работы фильтра Калмана – это один из первостепенных вопросов, который должен стоять перед инженером при разработке ПО для подобных систем.

На поиск необходимой информации по валидации фильтра Калмана у меня ушло больше недели, но результат того стоил. Поэтому в данной статье я хочу поделиться алгоритмом, который позволяет находить неочевидные ошибки в коде фильтра Калмана и определять возможности применения фильтра к конкретной задаче. 

Фильтр Калмана

Я предполагаю, что читатель знаком с базовыми принципами работы фильтра Калмана, поэтому лишь коротко объясню его суть. Для тех, кто не знаком, советую прочитать эту или эту статью.

Вкратце работу фильтра Калмана можно объяснить так:

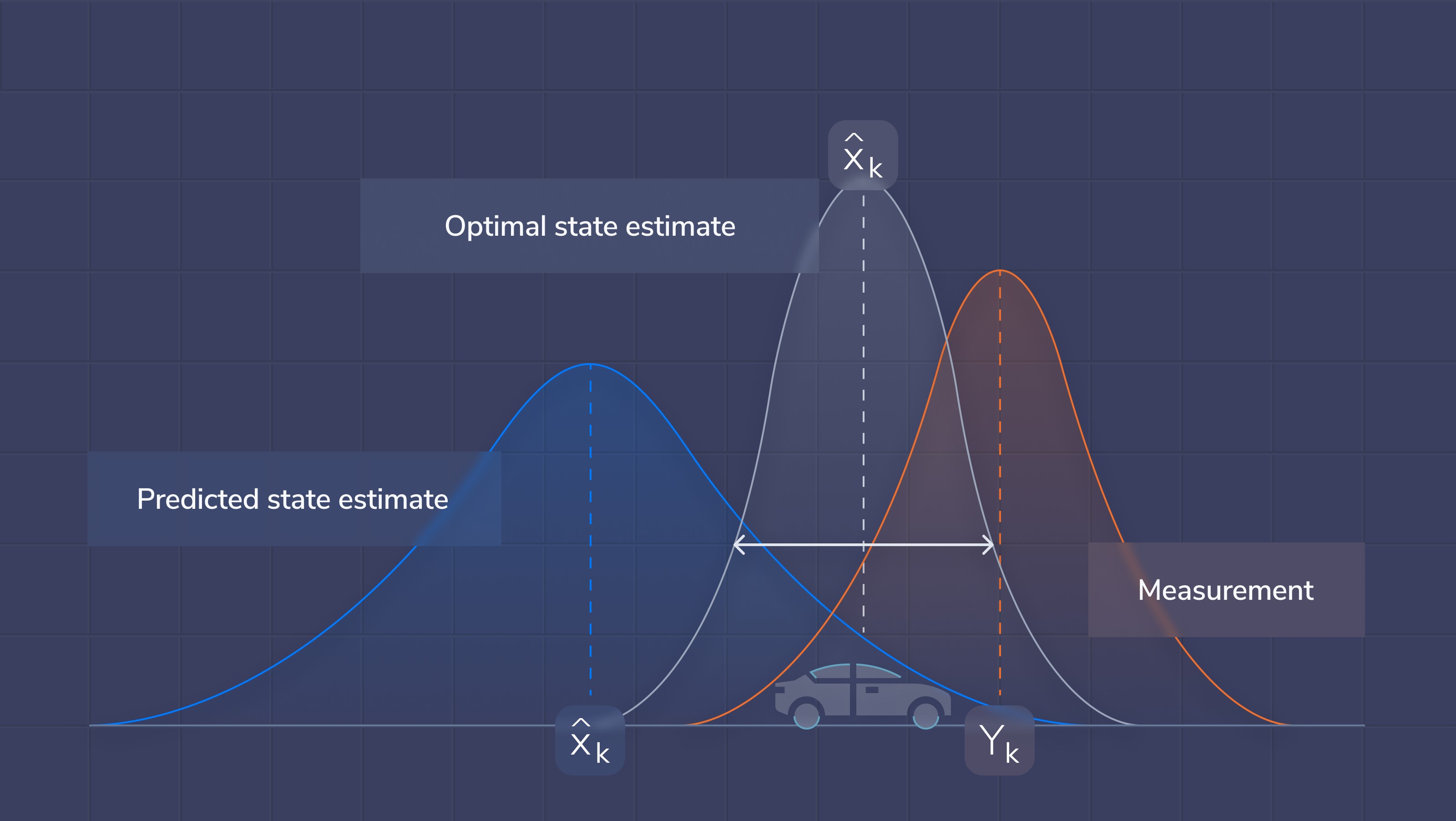
Для описания какого-либо процесса мы используем как состояние, полученное посредством измерений (Measurement), так и состояние, полученное по уравнениям, описывающим происходящий процесс (Predicted state estimate). Комбинируя эти два независимых состояния, мы получаем более точное оптимальное состояние (Optimal state estimate). 

В качестве измерений могут служить, например, измерения GPS-датчика в автомобиле, а движение машины может быть описано с помощью кинематических или динамических уравнений, которые по текущей скорости, углу поворота колес, ускорению и прочим характеристикам, могут определить прогнозируемое положение автомобиля в следующий момент времени. 

В зависимости от сложности процесса и измерений можно использовать линейный, расширенный или сигма-точечный фильтр Калмана.

Проблема верификации результатов

Фильтры Калмана используются в том случае, если мы имеем зашумленные измерения, а уравнения, описывающие динамику системы, известны лишь приблизительно. Алгоритмы, использующие фильтры Калмана, относятся к более общему классу оценочных алгоритмов, которые помимо состояния также оценивают возможную ошибку (с помощью ковариационной матрицы ошибок, например).

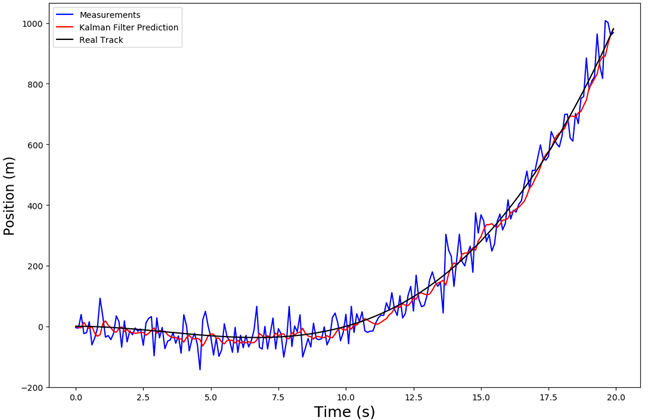
Есть множество материалов, статей, диссертаций, которые рассматривают существующие или разрабатывают новые разновидности фильтра Калмана, однако, вопрос валидации результатов встречается намного реже. Зачастую авторы ограничиваются сравнением зашумленного/оценочного/реального состояния, как это показано на рис. 2 (источник), аргументируя точность фильтра близким значением оценочного и реального состояний и забывая про ковариационную матрицу ошибок. Проблема такой оценки кроется в том, что без использования ковариационной матрицы ошибок мы не можем оценить, насколько точные данные мы имеем. 

Проиллюстрируем проблему на простом примере, когда состояние системы описывается одной переменной x. В таком случае, ковариационная матрица ошибок представляет из себя дисперсию σ_x² этой величины. Допустим, у нас x = 0 и σ_x = 1, тогда в соответствии с правилом 3 сигма, мы можем с уверенностью > 99.5 % сказать, что наша величина лежит в интервале [-3, 3]. Если мы увеличим среднеквадратичное отклонение σ_x до 10, то интервал увеличится до [-30, 30]. Если наш фильтр дает оценку x = 0 и σ_x = 1, в то время как действительная величина среднеквадратичного отклонения σ_x = 10, то наш объект может в реальности оказаться в местоположении, которое практически невозможно в соответствии с оценкой нашего фильтра. Чем это может грозить, думаю понятно без комментариев. Таким образом, дисперсия вносит существенный вклад в оценку состояния, и пренебрегать ей ни в коем случае нельзя.

С другой стороны, так как фильтр работает со случайными данными, то вполне возможно, что для какого-то набора данных даже некорректный фильтр выдаст правдоподобные результаты, поэтому делать выводы о том, как работает фильтр, по одному запуску было бы неверно. Кроме того, возникает вопрос: как убедиться, что значения дисперсии, рассчитанные по алгоритму, близки к реальным данным?

Терминология и обозначения

Прежде чем пойти дальше, введем основные обозначения и терминологию. Подстрочный индекс k будет обозначать номер временного слоя, x_k – вектор состояния системы, y_k – вектор измерений, P_k – ковариационная матрица ошибок, x₀, P₀ – начальные значения вектора состояния и ковариационной матрицы. Динамика системы описывается дискретными уравнениями:

где f – функция перехода для рассматриваемого процесса, w_k – некоторая матрица шумов, ассоциированная с соответствующей функцией перехода. Функция f может иметь различный вид, например, в простейшем случае быть линейной как относительно x_k-1, так и относительно w_k.

Связь между измерениями системы и вектором состояния описываются уравнением:

где h – функция, связывающая вектор состояния с вектором измерений, а v_k – некоторая матрица ошибок измерений.

Стоит отметить, что в общем случае размерности вектора измерений и вектора состояния различны. Например, состояние может в себя включать вектор положения и вектор скорости – итого 6 компонент, а измерения – только вектор положения, а значит, всего три компоненты.

Реальные значения вектора состояния и ковариационной матрицы мы будем обозначать x_k^* и P_k^*, в то время как значения, полученные с помощью фильтра Калмана, – просто x_k и P_k.

Постановка численного эксперимента

Для валидации фильтра Калмана мы будем использовать метод Монте-Карло. Вначале мы вычислим реальные значения состояния x_k^* на каждом временном слое от 0 до n. Для практических целей это можно сделать с помощью уравнения (1), заменив w_k на нулевую матрицу и задав определенные x₀^*, P₀^*.

Затем нам нужно смоделировать m независимых численных экспериментов. Всего у нас имеется 3 источника случайности, которые мы будем варьировать за каждый проход итерации Монте-Карло, – это начальное состояние (его мы знаем только с точностью, определяемой ковариационной матрицей P₀), и значения шумов, определяемые матрицами w_k и v_k. Таким образом, на каждом прогоне мы получаем различные значения начального состояния и значений шумов процесса и измерений на каждом временном слое. Номер итерации Монте-Карло мы будем обозначать буквой i. В результате моделирования мы будем иметь m произвольных наборов x_kⁱ и P_kⁱ для 0 ≤ k ≤ n и 0 ≤ i ≤ m.

Стоит заметить, что обычно при постановке задачи значения P_k^* не известны, однако их можно заменить на статистические значения, вычисленные по формуле:

где надстрочный индекс T – обозначает транспонирование. В дальнейшем везде под P_k^* имеется в виду P_k^est.

Верификация результатов

Стороннему наблюдателю может показаться, что мы ничего существенного не сделали, но, на самом деле, самое сложное уже позади. Осталось только понять, насколько близки значения x_kⁱ и P_kⁱ к ожидаемым значениям x_k^* и P_k^*. Для этого мы воспользуемся идеей из статьи [X. R. Li, Z. Zhao Measuring Estimator’s Credibility: Noncredibility Index // In Proceedings of 2006 International Conference on Information Fusion, Florence, 2006.], которая заключается в следующем: для каждого временного слоя k и для каждой итерации Монте-Карло i мы вычисляем noncredibility index по формуле:

Данная формула определяет некоторую ошибку как в случае несоответствия x_kⁱ, так и в случае несоответствия P_kⁱ, и обладает следующими полезными свойствами:

1. Значение γ_kⁱ близко к нулю, если x_kⁱ и P_kⁱ близки к действительным значениям;

2. Значение γ_kⁱ безразмерно и, следовательно, не зависит от единиц измерения x_kⁱ;

3. Значение γ_kⁱ одинаково серьезно штрафует как за оптимистичные (отношение [x_k^{i, err} P_kⁱ x_k^{i, err}] / [x_k^{i, err} P_k^* x_k^{i, err}] > 1) значения, так и за пессимистичные значения P_kⁱ (когда это отношение меньше единицы).

Тогда для временного слоя k можно посчитать среднее значение noncredibility index’а:

Это и есть основная мера валидности результата, полученного с помощью фильтра Калмана. Таким образом, для каждого временного слоя мы можем посчитать γ_k^avg и по нему понять, насколько хорошо работает наш фильтр. В процитированной работе было показано, что значения γ_k^avg ~ 1 соответствуют достоверным результатам.

Собирая все в одну кучу

Весь процесс валидации фильтра Калмана сводится к следующим шагам: 

1. Для поставленной задачи задаем функцию перехода f, функцию, связывающую вектор состояния с вектором измерений, h, матрицы шумов w_k и v_k и начальные значения x₀^*, P₀^*;

2. Проводим симуляцию без шумов для получения действительных значений x_k^*;

3. Запускаем m итераций Монте-Карло и получаем x_kⁱ и P_kⁱ для каждого временного слоя k и для каждой итерации i;

4. Вычисляем P_k^est в соответствии с формулой (5). P_k^est будет служить в качестве P_k^* ;

5. Для каждого временного слоя вычисляем γ_k^avg, которая и будет показателем достоверности результатов;

6. (Опционально) Строим график зависимости γ_k^avg от времени и смотрим, как изменялось качество работы фильтра.

Результаты

В качестве примера рассмотрим задачу отслеживания мотоцикла (рис. 3) из статьи.

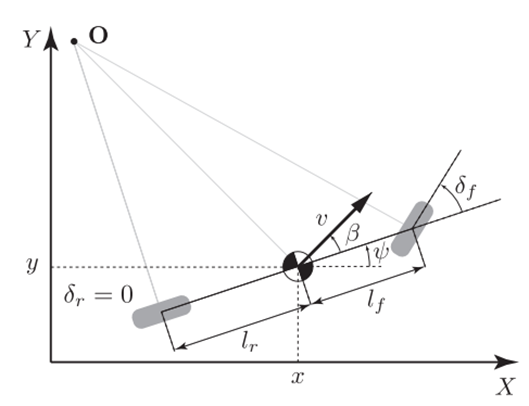
Уравнения, описывающие кинематическую модель движения, запишутся в виде:

где x, y – координаты центра тяжести, v – скорость, ψ – угол между направлением мотоцикла и осью x, β – угол между направлением скорости и направлением мотоцикла, a – ускорение, l_r и l_f – длина от центра масс до задней и передней части соответственно, δ_f – угол между направлением переднего колеса и направлением мотоцикла.

Значения l_r и l_f являются входными параметрами конфигурации мотоцикла, δ_f и a – значения, которые определяют динамику системы, а x, y – вектор состояния.

Из вида уравнений видно, что они имеют нелинейный вид, а следовательно, нужно применять либо расширенный, либо сигма-точечный фильтр Калмана.

Ради теста фильтров и для усложнения задачи с вычислительной точки зрения, будем считать, что измерения производятся в полярных координатах:

Измерения в полярных координатах вносят существенные нелинейности в расчеты и являются неплохой проверкой работы фильтра.

К сожалению, точные результаты работы для разрабатываемой библиотеки, которые можно было бы продемонстрировать, я опубликовать не могу. Однако, приведу здесь основные закономерности, которые были мной замечены при верификации фильтров Калмана. 

Ключевое, что хотелось бы отметить: несмотря на близость реальных и полученных данных состояния, благодаря данной схеме валидации, были выявлены участки кода, в которых происходила потеря значимых разрядов для чисел одинарной точности как для расширенного, так и для сигма-точечного фильтра Калмана. Для чисел с одинарной точностью график зависимости вид, подобный изображенному на рис. 4.

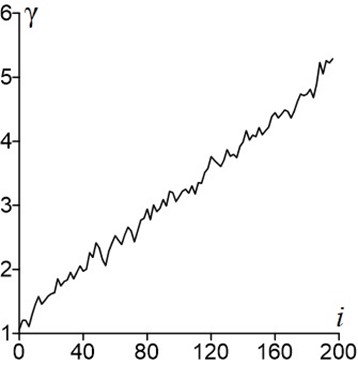
Как видно, значение noncredibility index растет с течением времени, что говорит о накапливаемой ошибке в результатах и, по-видимому, все большему удалению матрицы P_k от действительного значения. 

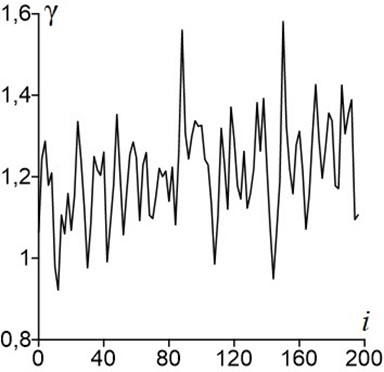
Для чисел двойной точности значения γ_k^avg от номера итерации колебались в пределах от 0.8 до 1.6, что говорит о правдоподобности результатов (см. рис. 5). Как видно из рисунка, значения noncredibility index не растут с течением времени, а лишь колеблются в окрестности некоторого среднего значения.

Вывод

В статье была разобрана достаточно простая задача, однако предложенный подход валидации легко обобщить как для более сложных постановок задач, так и для более комплексных подходов проведения численного эксперимента.

При применении рассмотренной выше схемы валидации для ряда более сложных задач мы установили, что расширенный фильтр дает неудовлетворительные результаты, которые было бы невозможно определить «на глаз» простым сравнением графиков векторов состояния. Таким образом, для дальнейшего моделирования мы использовали сигма-точечный фильтр.  

Лично меня подкупила простота подхода – какова бы ни была задача: со сложными дифференциальными уравнениями, описывающими процесс, и большим вектором состояния, или простыми алгебраическими уравнениями и скалярным состоянием, в итоге мы получаем лишь одно число, которое наглядно показывает, насколько хорошо фильтр описывает происходящий процесс. Другой плюс рассмотренного подхода – это возможность валидации не только вектора состояния x_kⁱ, но и ковариационной матрицы ошибок P_kⁱ.

Описанный подход также обладает достаточной общностью и может быть применен на более широкий круг фильтров, нежели фильтры Калмана.