
Изображение с сайта Mathematical Art Galleries
В этой серии из двух статей я приглашаю вас заглянуть в один любопытный и не самый популярный уголок математики, в котором обитают необычные создания — p-адические числа, а попутно хочу рассказать о написанной мной Haskell-библиотеке для работы с ними, а также о двух классных инструментах: о типах-литералах (type literals) и семействах типов (type families), приближающих нас к заветным зависимым типам.
Я люблю язык Haskell и, начиная с какого-то времени, мне стало комфортно думать на нём, особенно, на математические темы. Когда понадобилось освоить новый инструмент, — p-адические числа, оказалось, что в репозитории hackage, основном для Haskell-сообщества, нет инструментов для работы с ними, даже в таких серьёзных теоретико-числовых библиотеках, как arithmetic, arithmoi или factory. В конце концов, я написал и опубликовал свой модуль padic, и во второй части этой серии расскажу о некоторых деталях его реализации. А сейчас речь пойдёт о самих p-адических числах.
В арсенале профессионалов и настоящих мастеров подчас попадаются странные инструменты. Не сразу можно сказать для чего они нужны и как они, вообще, могут быть полезными. Но при решении каких-то особенных задач они оказываются незаменимыми. Начиная с какого-то уровня погружения в теорию чисел, алгебраическую геометрию, квантовую механику или теорию струн, авторы книг и статей зачастую переходят от привычных целых и вещественных чисел к p-адическим числам и при этом удивительным образом чувствуют, что им становится легче. У меня, по крайней мере, первое знакомство с ними ощущения лёгкости не создало. В сети достаточно много вводных материалов по этой теме, как виде книг, статей и блогов, так и в форме видео. Большинство из этих введений начинается либо с введением бесконечноразрядных чисел, либо с определения p-адической нормы, а завершается упоминанием фрактальной (канторовой) топологии, которую эти числа образуют. При этом приводится пара канонических примеров необычности этой числовой системы, таких как сходимость суммы всех положительных степеней двойки к минус единице или возможность получить целочисленные квадратные корни из ,
или
. В более серьёзных книгах всё внезапно становится существенно более сложным, поскольку авторам вдруг становится важно не то как складывать и умножать эти числа, а то что они образуют проективный предел колец вычетов относительно естественных проекций или что образуемое ими метрическое пространство неархимедово. Это похоже на ситуацию с многочисленными введениями в монады, или на известный мем с рисованием совы. Поэтому мы сегодня, отталкиваясь от вполне понятных и несложных вещей, постараемся пройти несколько дальше и понять в чём практический смысл введения этих числовых монстров.
Начинаем с цифр
Что мы имеем в виду, когда записываем число рядом цифр? То, что его можно представить в виде взвешенной суммы степеней некоторого основания, натурального числа, не равного нулю или единице. Как правило, мы работаем с основанием , равным числу пальцев на руках, в «цифровом» мире повсеместно используется самое маленькое из возможных основание
, ну, а при записи времени нам оказалось удобным использовать смешанную систему с основаниями
и
.
В позиционной записи числа цифры выбираются из конечного множества возможных остатков деления на основание, а позиция цифры в ряду, обозначающем число, соответствует степени основания. Это всё привычно и поэтому кажется простым. Более того, в повседневности мы складываем и вычитаем, умножаем и делим, а также сравниваем не числа, а их позиционную запись (расширенную знаком «минус» для отрицательных чисел), а это значит, мы рассчитываем на то, что множество чисел и множество их позиционных представлений «работают» одинаково. Если мы выберем в качестве представления числа не цепочки цифр, а какие-то количественные меры, например, шаги на бесконечной ленте, то результаты сложения «в столбик» и непосредственно шагами на этой ленте будут согласованы между собой. Это же относится и к другим числовым операциям и свойствам. Говоря на языке математики, мы рассчитываем на изоморфизм между двумя числовыми системами: системой целых чисел и системой, которое образуют последовательности цифр вместе со знакомыми нам со школы операциями поразрядного сложения, вычитания и умножения.
Наконец, и сами цифры при выполнении арифметических операций тоже ведут себя как элементы своей числовой системы. Это значит, что цифры тоже можно складывать, вычитать и умножать, но по особым правилам модулярной арифметики, у которой тоже есть хорошо знакомый нам «нецифровой» аналог: шаги по замкнутой ленте.
Далее я буду использовать математические имена и обозначения для этих числовых систем. Система целых чисел (изоморфная шагам по бесконечной в обе стороны ленте) является кольцом и обозначается Цифры, используемые при записи числа в позиционной записи с основанием
образуют кольцо вычетов по модулю
, которое мы будем обозначать как
. Эта система изоморфна шагам по замкнутой ленте, вмещающей ровно
ячеек или отметок.
В кольце можно складывать, вычитать и перемножать любые элементы, получая результаты, принадлежащие этому же кольцу. А вот деление возможно не всегда, например, в кольце нет такого элемента, который был бы равен
, то есть, решал бы уравнение
. Для того, чтобы можно было делить на любой ненулевой элемент, кольцо
расширяется до поля рациональных чисел
.
Кольца вычетов конечны, и может показаться, что их возможности меньше бесконечного кольца целых чисел, но это не так. В них, даже в совсем небольших, можно обнаружить то, чего нет в целых числах. Например, в кольце из пяти элементов
у каждого элемента есть противоположный, то есть такой, что в сумме они дают ноль. То есть, в этом смысле оно включает в себя «отрицательные числа»:
. Более того, в этой системе у любого корректного линейного уравнения есть решение, то есть, у каждого ненулевого элемента есть обратный, такой, что их произведение равно еднице. Таким образом, оно содержит в себе все возможные формальные дроби:
. Значит, это уже не только кольцо, но и поле. Каждое кольцо вычетов по модулю, являющемуся простым числом, образует поле.
Но это ещё не все «сокровища». В кольце есть то, чего нет ни в целых, ни в рациональных числах, например, решение уравнения
, то есть,
, ведь
. Это, впрочем, вовсе не значит, что
— это мнимая единица, это вполне рядовой элемент конечного поля.
Кольца вычетов разные и у каждого есть свои интересные особенности, например, в кольце привычных нам цифр нет всех возможных дробей, но зато в нём есть делители нуля, то есть, такие ненулевые числа, которые в произведении дают 0 (например,
). А ещё в нём есть числа, равные своим квадратам: это
и
(помните рифмы в таблице умножения: «пятью-пять — двадцать пять, шестью-шесть — тридцать шесть»?). Таким образом, уравнение
имеет в этом кольце целых четыре различных корня из которых два нетривиальны!
Поднимаемся выше
Каждое кольцо вычетов порождает целое семейство «потомков», которым они передают часть своих особенностей, но которые способны пойти дальше своего «родителя». Потомками кольцá можно считать кóльца
,
и т.д. Рассмотрим, например, кольцо
. В нём, как и у его родителя
тоже есть все противоположные числа и большая часть дробей (кроме тех, что имеют знаменатель, кратный
). Имеется в нём и
, а также появляются корни из
и
, которых не могло быть в
. В ещё большем кольце
остаётся всё то же, что было у «предков», но расширяется набор квадратных уравнений, имеющих решения и появляется возможность решать некоторые кубические уравнения.
А интересно, если продолжать наращивать степени и новые возможности, то какими свойствами будет обладать кольцо ? На этот вопрос и ответил Курт Гензель, определив для такого предельного кольца числовую систему и описав его свойства. Система
, порождаемая кольцом вычетов
называется системой целых p-адических чисел и обозначается
. Она включает в себя всех своих родителей, как подкольца и обладает всеми их свойствами сразу!
Получается, что можно построить цепочку числовых систем:
с помощью простой операции вычисления остатка (она показана стрелкой). У этой цепочки есть два предела — прямой: и обратный (или проективный) —
. Таким образом, система p-адических чисел является системой, обладающей универсальным свойством: из неё можно построить гомоморфизм в любое конечное кольцо вычетов по модулю
.
При устремлении к бесконечности, количество переходит в качество, и мы получаем нечто новое: бесконечное кольцо, которое включает в себя не только конечные подкольца, но и всё целиком, и кроме того, все формальные дроби со знаменателями, не кратными основанию
, а также решения широкого класса алгебраических уравнений линейных, квадратных и высших степеней! Не любых, конечно, а только тех, что решаются в кольцах-родителях, но это «не баг, а фича», поскольку позволяет относительно легко ответить на вопрос о существовании решения у заданного алгебраического уравнения, который в целых или рациональных числах представляет крайне сложную задачу. Достаточно вспомнить, Великую теорему Ферма о существовании решения уравнения
в целых числах при
, достаточно жестко ограничивает нас в выборе доступных математических инструментов. Его можно изящно обойти, используя приём хорошо знакомый физикам и инженерам: разбить число на мантиссу и экспоненту. Любое рациональное число можно разложить в произведение
, в котором число
— обратимое целое p-адическое число (для которого всегда можно вычислить
), а
— показатель степени при основании
. Таким образом, рассматривая числа
и
, мы всегда сможем найти их отношение
. Этот приём позволяет нам дополнить кольцо целых p-адических чисел
до поля рациональных p-адических чисел
. Если
— простое число, то у нас этот трюк точно получится, поскольку в этом случае кольцо
не содержит делителей нуля, которые обязаны в случае простого
содержать в себе его в качестве множителя. Однако все такие множители мы вынесли в выражение
, а значит, любое число
будет обратимым.
При работе с позиционными системами счисления выгодно в качестве основания выбирать число с большим количеством множителей, это упрощает таблицу умножения. Число в этом отношении не оптимальное, основания
,
или
существенно выгоднее и все они используются человечеством, как основания с древнейших времён. Однако для работы с p-адическими числами составные основания хуже простых, поскольку не дают преимуществ поля. Так что часто в самом начале статей и книг сразу оговаривают, что число
в p-адической системе — простое.
Итак, несложный трюк помог нам повысить статус p-адических чисел до полноценного поля, которое теперь включает в себя в качестве подкольца целиком всё кольцо целых чисел , а в качесте подполя целиком всё поле рациональных чисел
, а помимо них бесконечное множество других элементов, решающих алгебраические уравнения!
Конечные поля вычетов (алгебра простых цифр), которые лежат в основе p-адических чисел, существенно проще для анализа чем натуральные числа. Там, конечно, тоже хватает технических трудностей, но к ним проще подступиться потому, хотя бы, что поля эти конечны. Очень многие общие результаты теории чисел и алгебраической геометрии могут быть получены переходом к 2-адическим числам, которые, как мы теперь понимаем, можно рассматривать как бесконечноразрядные двоичные дроби.
Но, возникает вопрос: откуда же взялись все эти дополнительные числа? Описанный нами процесс повышения степени колец вычетов всё время расширял кольца новыми целыми числами, принадлежащими кольцам . Все наши формальные дроби и квадратные корни всегда совпадали с какими-то целыми числами и были от них неотличимы. Значит ли это, что и в
дроби и алгебраические корни тоже будут какими-то целыми числами, совпадающими с «нормальными». И да и нет. Да — они все будут целыми, нет — они все будут отличаться и друг от друга и от элементов подкольца
. Тут работает магия предельного перехода.
Возвращаемся к цифрам
Что мы делаем, когда хотим выразить сложную мысль? — используем много букв. А если нужно выразить большое целое число? — тогда нужно использовать много цифр и позиционную запись. С помощью привычной нам позиционной системы счисления можно выражать и p-адические числа.
Начём опять с маленького кольца . Все его элементы принадлежат множеству цифр
. Поднимемся на ступень выше и перейдём в кольцо
. Можно каждому элементу этого кольца назначить свой символ, скажем, из английского алфавита, а можно воспользоваться тем, что в этом кольце ровно
элементов, ни больше ни меньше, а значит каждому из них можно поставить в соответствие пару цифр, и таких пар будет в точности
. Это соответствие можно сделать не каким попало, а естественным, то есть таким, которое сможет сохранить числовые свойства цифр и элементов
. Для этого достаточно использовать принципы позиционной записи, представив числа из
как сумму
используя цифры
. Получим хорошо знакомую пятиричную систему счисления, которая позволяет подниматься по степеням основания, повышая разрядность записи числа. Так для записи любого числа из
потребуется цепочка из
пятиричных цифр.
Самое главное достоинство такого представления состоит в изоморфизме между числами и их позиционном представлении, о котором говорилось в самом начале статьи. Благодаря ему арифметические операции, производимые поразрядно (сложение с переносом, вычитание с «заниманием», умножение «в столбик» и деление «уголком») согласуются с арифметикой чисел, представляемых цепочкой цифр. А это значит, что совершая предельный переход от конечных колец к бесконечному, мы получаем возможность записывать 5-адическое число с помощью бесконечной цепочки пятиричных цифр:
и автоматом получаем практическую арифметику для p-адических чисел, знакомую со школьной скамьи! Такая запись называется каноническим разложением p-адического числа. И как только число разрядов устремляется к бесконечности, у нас и появляется куча свободного места для дополнительных чисел.
Все целые числа записываются конечным числом цифр. Задумайтесь над этим, множество целых чисел не ограничено сверху, однако сколь бы большое число вы ни выбрали (хоть знаменитое число Грэма, хоть его факториал) оно всегда может быть представлено конечным числом цифр. Таким образом, любое целое число можно представить как p-адическое, добавив бесконечную цепочку нулей после старшего разряда. Но p-адические числа могут иметь и любые ненулевые числа в своём бесконечном хвосте, который, по нашему определению, бесконечно длинее любой конечной цепочки цифр в начале. Таким образом, множество p-адических чисел много больше множества целых! Настолько же, насколько множество иррациональных чисел больше множества рациональных. Бесконечное разнообразие бесконечных последовательностей из конечного набора цифр образует континуум!
При переходе к рациональным p-адическим числам, мы вводим аналог десятичной точки, которая разделяет p-адическое число в каноническом разложении на конечную дробную и бесконечную целую части. Так что число можно записать как
, в полном согласии с нашей интуицией.
Давайте посмотрим на примеры некоторых p-адических чисел:
В каноническом p-адическом разложении целые числа записываются в виде конечной последовательности цифр (бесконечную цепочку нулей, уходящую налево при записи опускают). Отрицательные целые числа вместо бесконечной цепочки нулей слева имеют бесконечную последовательность наибольшей из цифр (сравните с тем, как в двоичной системе представляются отрицательные числа). В p-адическом разложении цифры рациональных чисел после какой-то конечной цепочки всегда приходят к периодической последовательности. Обратите внимание на то, что запись числа в десятичной дроби и в виде 10-адического числа совпадают, это не случайно и достаточно удобно: положительные целые и дробные числа с конечным числом цифр имеют одинаковые десятичное и 10-адическое представление.
Какая от них польза?
Если долго смотреть на бесконечный хвост, уходящий влево, становится не по себе, ведь чем левее цифра, тем старше разряд, то есть, тем больше число. Получается, что почти все p-адические числа в обиходном смысле «бесконечны». Впрочем, «бесконечных» чисел в математике не существует, смысла в них немного. Как же вопринимать числа, записываемые заведомо бесконечным числом разрядов? В некотором смысле, так же, как и числа с бесконечным числом разрядов, но только уходящих направо от десятичной запятой, как в десятичных дробях, к ним-то мы привыкли! Вполне безобидное конечное число имеет в десятичной позиционной системе бесконечную последовательность цифр
, так же как и в 10-адической:
. Множество рациональных чисел в десятичной записи тоже включает в себя все натуральные числа, как такое подмножество, у которого справа от десятичной точки начинается бесконечная цепочка нулей. При этом большая часть вещественных чисел, образующих континуум, может быть записана только в виде бесконечной последовательности ненулевых цифр. Так что же, p-адические числа это как p-ричные дроби, записанные наоборот? Простая формальность? Нет, это не так, они круче!
В некоторых популярных введениях p-адические числа презентуют, как «бесконечноразрядные числа», или как оригинальный способ записывать числа «в обратном порядке» относительно привычно дробной десятичной нотации. Но надо понимать, что цепочки цифр — это не числа, они образуют вполне самостоятельную алгебраическую структуру, изоморфную (при определённых условиях) той или иной числовой системе. Большую часть вещественных чисел составляют невычислимые числа, для которых неизвестен способ их представления в форме цепочки цифр или даже в форме комбинации из вычислимых чисел. Каноническое разложение p-адического числа — это не p-адические число, а одно из его представлений, причём, только для вычислимых чисел и, к тому же, не самое удобное или эффективное, просто оно интуитивно понятно в силу нашей привычки оперировать позиционной нотацией. Самое главное, p-адические числа не являются представлением привычных нам целых, рациональных или вещественных чисел, они образуют самостоятельную алгебраическую систему, в которой есть образы инъективных гомоморфизмов (однозначных отображений) из систем вещественных чисел, но есть и иные объекты, у которых нет никаких вещественных аналогов.
Это важное замечание. Существование однозначного отображения любого рационального и многих алгебраических чисел в p-адическое поле, не гарантирует, что результат вычислений, произведённых с образами этих чисел, имеет вещественный аналог. Например, в кольцах с делителями нуля существуют нетривиальные автоморфные числа (числа, которые не меняются при возведении в произвольную натуральную степень). В вещественных и комплексных числах этими свойствами обладают только и
, а, например, в
есть ещё два таких числа:
и
, мы встречали их «родителей» (
и
) в базовой модулярной арифметике
. А в
таких чисел уже шесть! И ни одному из них не удастся найти прообраза ни в
ни в
. Впрочем, если основание простое и мы имеем дело с p-адическим полем и нормальной арифметикой, то нетривиальных автоморфных чисел уже не будет, но там будут иные диковинные звери, обитающие только в этих полях.
В общем, перейти p-адический мир не трудно, а вот вернуться оттуда можно не всегда. Это не так уж и необычно, для числовых систем. Множество вещественных чисел включает в себя множество рациональных
, но кроме него
содержит в себя все пределы фундаментальных последовательностей, сходящихся в
, но не ему принадлежащих. Классические примеры таких пределов:
. Первое можно получить как предел последовательности конечных цепных дробей или шагов метода Ньютона, а второе и третье — в виде последовательности частичных сумм рядов Тэйлора и Лейбница. Все без исключения элементы этих последовательностей рациональны, а их пределы — нет. И рациональных аналогов этим числам найти не удастся. Таким образом, добавляя к
все возможные пределы сходящихся последовательностей из элементов
, мы пополняем его до чего-то принципиально большего.
Такое же ключевое свойство, отличает множество от сколь угодно больших, но конечных колец
, породивших его. Оно включает в себя все пределы сходящихся последовательностей из своих элементов (сходящихся в особом, p-адическом смысле). Это позволяет рассуждать о непрерывности и задействовать ряд методов анализа, основанных на понятиях пределов и производных: метод Ньютона, ряды Тэйлора, а вслед за этим экспоненты, логарифмы, тригонометрию, гамма- и дзета-функцию и прочие инструменты! Все они будут заметно отличаться от своих вещественных аналогов, сохраняя, впрочем, свои главные свойства, и работать смогут не всегда, но их наличие очень важно, когда речь заходит о серьёзной работе с числовыми системами.
Наконец, поле можно алгебраически замкнуть, расширив его корнями алгебраических уравнений и превратив в поле p-адических комплексных чисел
, а оно уже оказывается изоморфным полю комплексных чисел, построенному на основе вещественных чисел. То есть, наряду со стандартной цепочкой вложений числовых систем:
можно строить альтернативные цепочки
которые начинаются с конечных полей вычетов, и достигают алгебраического замыкания, минуя поле . Между этими цепочками есть сложные родственные связи: любое кольцо
включает в себя кольцо
, а поле
имеет подполем
. Однако если мы устремим
к бесконечности, то и
и
станут изоморфны
— множеству натуральных чисел, то есть, множеству цифр в
-ичной системе счисления (до второй цифры в каноническом разложении дело так и не дойдёт).
В середине XX века Александр Островский доказал, что иных путей, ведущих к полным алгебраическими числовым системам не существует. Это значит, что мы перечислили все возможные числовые системы, содержащие свободное кольцо, изоморфное кольцу целых чисел, свободное поле, изоморфное полю рациональных чисел, а также их пополнение и алгебраическое замыкание.
Есть ещё один практический аспект, делающий p-адические числа полезным инструментом и за пределами чистой теории чисел. Одна из досадных неприятностей при вычислении чисел в позиционной записи состоит в несимметричности операции переноса — он всегда делается от младшего разряда к старшему, то есть, справа налево. В этом отношении бесконечный «хвост» цифр, уходящий налево принципиально лучше бесконечного «хвоста», уходящего направо. Ведь переносы приходят именно справа, так что переполнение разряда где-то далеко в бесконечном ряду цифр при любой арифметической операции, может, в принципе, передаваясь по цепочке, повлиять на сколь угодно большой разряд. По существу, каждая цифра, действительного числа, вычислимого в позиционной записи, хранит потенциально бесконечную информацию о всех своих соседях справа. С этим связаны проблемы округления и вытекающая из них неустойчивость вычислительных алгоритмов, а также то, что дробные числа могут иметь два различных позиционнных представления, например, . Это значит, что отображение между рациональными числами и их позиционным представлением не биективно, и дело тут уже не в округлении, а гораздо глубже. Это нарушение биективности до сих пор не даёт некоторым математикам (например, Норберту Уайлдбергеру) покоя и они ищут возможность избавиться от него.
В тоже самое время, арифметические действия, выполняемые поразрядно над целыми числами, которые «растут» только влево, не могут повлиять на цифры, которые уже вычислены. Обрывание цепочки где-то далеко слева никак не изменит уже известных нам младших разрядов.
На практике это заключается в следующем. Работая с числами с плавающей точкой, мы постоянно чувствуем конечность разрядности наших вычислительных машин:
> 0.2 + 0.1
0.30000000000000004Знакомо? При этом неважно с какими числами мы работаем, с большими или маленькими, ошибки округления неизбежны, и, если можно так выразиться, плотно обступают любые числа. В то же самое время, конечность разрядов в целочисленных типах никак не влияет на точность вычислений для чисел, далёких от верхней границы, которая для или даже
разрядной арифметики уже весьма и весьма велика! Потому так ценятся целочисленные алгоритмы, могущие заменить возню с плавающей точкой. Превращая рациональные числа в p-адические, мы переводим их в область целых чисел, в которой обрывание бесконечной цепочки цифр слева, не затрагивает цифры, уже полученные в более младших разрядах.
В этой основательной статье, которую я рекомендую всем заинтересовавшимся данной темой, приводится пример вычислительной устойчивости стандартных матричных операций в действительных и в p-адических числах. Вот, например как меняется число верных цифр при обращении матрицы Гильберта, простой, но неприятной матрицы, содержащей простые дроби. В обоих случаях использовалось одинаковое число бит для конечного представления числа.
| Размер матрицы | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 50 | 100 |
| IEEE | 40 | 34 | 28 | 25 | 19 | 14 | 9 | 4 | 0 | – | – |
| ℚ2 | 52 | 52 | 51 | 51 | 51 | 51 | 51 | 51 | 51 | 49 | 48 |
Всё это выглядит впечатляюще, но отчего мы до сих пор не отказались от чисел с плавающей точкой и не перешли на p-адические числа, раз уж мы всё равно используем похожие на них двоичные числа для оцифровывания всего на свете? Всё дело в топологии.
Почему мы не проходим p-адические числа в школе?
Топология — это не только про бублики и бутылки Клейна, как может показаться после знакомства с популярными введениями, она про такие свойства пространств и математических объектов, как непрерывность, связность, про их метрические свойства и отношения между объектами, сохраняющие эти свойства.
Так вот с топологическими свойствами у системы p-адических чисел беда! Их нельзя выстроить по порядку вдоль прямой, как мы привыкли это делать с целыми, рациональными или вещественными числами. Расстояние между двумя p-адическими числами, то есть, абсолютное значение их разности, которое позволяет рассуждать о точности вычислений и о сходимости последовательностей, может быть вычислено единственным способом и он абсолютно не согласуется каким-либо порядком в . Более того, «между» любыми двумя целыми p-адическими числами можно отыскать сколько угодно других целых p-адических чисел, которые в привычной метрике оказались бы не просто далеко, а бесконечно далеко друг от друга! Впрочем, я взял слово «между» в кавычки, потому что и оно не совсем корректно, ибо p-адические числа топологически размещаются не на каком-то гладком многообразии, а на древо-подобной структуре. При этом пересечение всех открытых интервалов (шаров) образует не континуум, как в топологии действительных чисел, а фрактальное несвязное канторово множество. Впрочем, и сами шары в топологическом p-адическом пространстве весьма странные: любая точка шара, в том числе и граничная, является его центром. Так что мыслить шагами или отрезками на числовой прямой, любо непрерывными перемещениями в пространстве никак не получится, а это очень важная деталь в математической картине физического мира, в котором малому относительному смещению двух точек в пространстве или времени соответствует малое изменение расстояния между ними. В p-адическом мире на это рассчитывать не приходится.
С чем же связана такая оригинальная топология? Нельзя ли было построить её как-нибудь иначе? Увы, теорема Островского утверждает, что существует только два способа построения нетривиального самосогласованного нормирования для числовых систем, один — привычный для нас вещественный, а другой — p-адический. Так что, говоря о p-адических числах совершенно необходимо разобраться как устроено p-адическое метрическое пространство. И в этом нам опять поможет позиционная запись.
Каким образом мы выясняем близки ли два вещественных числа друг к другу, если они представлены не кучками фасолин или отрезками на прямой, а цифрами? Начиная со старшего разряда, мы сравниваем между собой цифры этих двух чисел, и чем длиннее оказывается непрерывная цепочка совпадающих цифр, тем ближе друг к другу наши числа. Разница между двумя числами 123.456789 и 123.456689 существенно меньше, чем между 123.456789 и 113.456789, хотя в обоих случаях отличие состоит в единственной цифре. Всё дело в позиции отличающихся цифр. Разговор о расстоянии между числами проще вести если одно число равно нулю, тогда можно рассуждать об абсолютном значении и нормировании числа (англ. valuation), а для сравнения ненулевых чисел использовать абсолютное значение их разности. В мире вещественных чисел абсолютное значение совпадает с модулем числа. Так, разница между 123.456789 и 123.456689 составляет 0.0001, а между 123.456789 и 113.456789 — 10. Число 0.0001 ближе к нулю чем 10.00. По этой причине в сходящихся последовательностях вещественных чисел, выраженных в позиционной системе счисления, увеличивается число цифр, совпадающих в левой части числа. Вот, например, как выглядит приближение к числу методом Ньютона в вещественных числах:
1.0000000000000000
1.5000000000000000
1.4166666666666665
1.4142156862745097
1.4142135623746899
1.4142135623730950
А теперь перейдём в p-адический мир и перевернём всё задом-наперёд. Числа в каноническом представлении у нас имеют бесконечный хвост уходящий налево, при этом степень основания продолжает расти как росла, справа налево. Как же сравнивать такие числа? На первом курсе Университета ходила шутка: «Какое число больше или
, если читать их с конца?» Так вот, теперь это не шутка, а серьёзный вопрос.
Единственный способ сравнения, который нам остаётся, это такое же сравнение по цифрам, но совпадающие цифры мы можем считать только справа налево, начиная с младшего разряда. Вот, например, как выглядит приближение к тому же методом Ньютона, но в
:
…00000000000000000000000000000000000004
…51515151515151515151515151515151515154
…52300452300452300452300452300452300454
…02010030046244242322523014664645450454
…55641253041334120254404655400245450454
…16163312301130043502554655400245450454
…26305612301130043502554655400245450454
Последовательность, и правда, сходится, но в p-адическом смысле: с каждым шагом число не меняющихся цифр растёт, но в старших разрядах царит хаос. В пределе мы получим то самое целое число, которое при возведении в квадрат будет в точности равно 2, но путь к нему с точки зрения вещественного порядка будет выглядеть бешеным метанием по числовой оси. Если мы будем рассматривать разности между последовательными членами нашей приближений, то цепочки совпадающих цифры (выделенные жирным), превратятся в постоянно увеличивающуюся цепочку нулей. Именно так выглядит последовательность p-адических чисел, монотонно убывающая по их абсолютному значению. Формально абсолютное значение на определяют так:
, где
— это число нулей в правой части числа, то есть, позиция младшего ненулевого разряда числа. Например:
Элемент записывается в общем виде как
, при этом обратимый множитель
всегда имеет абсолютное значение равное 1, а
.
Округление p-адических чисел, таким образом, состоит в обрывании цепочки цифр слева. А благодаря тому, что при арифметических операциях перенос происходит от младшего разряда к старшему, при таком округлении мы не теряем никакой информации. Так что мы можем проводить вычисления с конечными округлёнными представлениями p-адических чисел, но, увы, из-за их патологической топологии мы не сможем ни построить график, ни, как-то вразумительно изобразить эти числа геометрически.
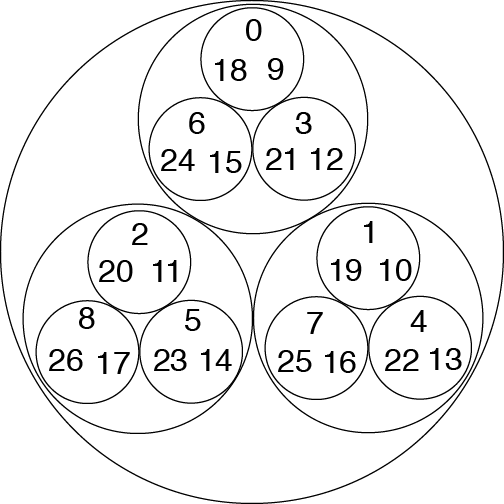
Эта диаграмма, показывает степень близости нескольких целых 3-адических чисел друг к другу. Если вы мысленно соедините стрелками числа, следующие по порядку, то получите представление о том, как действует на множество p-адических целых простейшая арифметическая операция: прибавления единицы. Как видите, даже такая элементарная операция катастрофически перемешивает точки в 3-адическом топологическом пространстве. На картинке в заголовке статьи показан пример визуализации прибавления единицы для 2-адических и 3-адических чисел. Промежуточное значение здесь имеет чисто демонстрационное значение, показывающее как одни целочисленные точки переходят в другие. А если мы вспомним, что кроме целых чисел в этом топологическом пространстве прячется целый континуум точек, образующих канторово множество, то станет понятно, что каким-либо внятным образом это множество и функции на нём изобразить не удастся.
Эти очень мощные, но очень специфические инструменты на практике используются, в основном, в теории чисел и абстрактной алгебре, но вот уже более полувека они стали рабочими лошадками в физике (квантовой механике, теории струн), в теории динамических систем и в методах генерации псевдослучайных чисел, в которых корявая p-адическая топология превратилась из неприятности в преимущество.
В следующей статье я расскажу о некоторых деталях реализации библиотеки для работы с p-адическими числами на языке Haskell и покажу ряд примеров работы с ними (тизер: мы вычислим число Грэма).


