
Математику часто называют «языком науки». Она хорошо приспособлена для количественной обработки практически любой научной информации, независимо от ее содержания. А при помощи математического формализма ученые из разных областей могут в какой-то степени «понимать» друг друга. Сегодня похожая ситуация складывается с Computer Science. Но если математика — это язык науки, то CS — её швейцарский нож. Действительно, трудно представить современные исследования без анализа и обработки огромных объемов данных, сложных вычислений, компьютерного моделирования, визуализации, применения специального ПО и алгоритмов. Разберем несколько интересных «сюжетов», когда разные дисциплины используют методы CS для решения своих задач.
Биоинформатика: от чашек Петри к биологии In silico
Биоинформатику можно назвать одним из самых ярких примеров стыка CS и других дисциплин. Эта наука занимается анализом молекулярно-биологических данных при помощи компьютерных методов. Биоинформатика как отдельное научное направление появилась в начале 70-х годов прошлого века, когда впервые были опубликованы нуклеотидные последовательности малых РНК и созданы алгоритмы предсказания их вторичной структуры (пространственного расположения атомов в молекуле).
С проекта «Геном человека» по определению последовательности нуклеотидов в ДНК человека и идентификации генов в геноме началась новая эра биоинформатики. Стоимость секвенирования ДНК (определение последовательности нуклеотидов) упала на несколько порядков. Это привело к колоссальному увеличению числа последовательностей в публичных базах данных. На графике ниже изображен рост количества последовательностей в публичной базе данных GenBank с декабря 1982 года по февраль 2017 в полулогарифмическом масштабе. Чтобы накопленные данные стали полезными их нужно каким-то образом проанализировать.

Рост числа последовательностей в GenBank c декабря 1982 по февраль 2017. Источник: www.ncbi.nlm.nih.gov/genbank/statistics
Одним из методов анализа последовательностей в биоинформатике является их выравнивание. Суть метода заключается в том, что последовательности мономеров ДНК, РНК или белков размещаются друг под другом таким образом, чтобы увидеть сходные участки. Сходство первичных структур (то есть последовательностей) двух молекул может отразить их функциональную, структурную или эволюционную связь. Так как последовательность можно представить в виде строки с определенным алфавитом (4 нуклеотида для ДНК и 20 аминокислот для белка), то выравнивание оказывается комбинаторной задачей из CS (например, выравнивание строк также используется в обработке естественного языка — NLP). Однако контекст биологии добавляет в задачу некоторую специфику.
Рассмотрим выравнивание на примере белков. Одному остатку аминокислоты в белке соответствует одна буква латинского алфавита в последовательности. Строки пишутся одна под другой, чтобы достичь наилучшего совпадения. Совпадающие элементы находятся один под другим, «разрывы» заменяются знаком «-» (гэп). Они обозначают индел, то есть место возможной вставки (внедрения в молекулу одного или нескольких нуклеотидов или аминокислот) и делеции (»выпадение» нуклеотида или аминокислоты).

Пример выравнивания аминокислотных последовательностей двух белков. Синим цветом выделены лейцин (L) и изолейцин (I), являющиеся изомерами — такая замена в большинстве случаев не отражается на структуре белка
Однако, как определить, оптимальное ли получилось выравнивание? Первое, что приходит в голову, это оценить количество совпадений: чем больше совпадений, тем лучше. Однако в контексте биологии это не совсем так. Замены (замещения одной аминокислоты другой) неравноценны: некоторые замены (например, S и T, D и E — остатки, отличающиеся по структуре ровно на один атом углерода) практически не отражаются на структуре белков. А вот замена серина на триптофан сильно изменит структуру молекулы. Для определения, является ли выравнивание лучшим из всех возможных, вводят количественный критерий (вес или счет). Для оценки замен используют так называемые матрицы замены, основанные на статистике замены аминокислот в белках с известной структурой. Чем больше число на пересечении сопоставленных букв, тем больше счет.

Периодически появляются новые матрицы замен. Здесь представлена матрица BLOSUM62
Счет также учитывает наличие делеций. Обычно штраф за «открытие» делеции на несколько порядков больше, чем за «продолжение». Это объясняется тем, что участок из нескольких идущих подряд гэпов считается за одну мутацию, а несколько гэпов в разных местах — за несколько. В примере ниже первая пара последовательностей более схожа, чем вторая, потому что в первом случае последовательности формально отделяет одно эволюционное событие:

Теперь о самих алгоритмах выравнивания. Выделяют два вида парного выравнивания (нахождение сходных участков двух последовательностей): глобальное и локальное. Глобальное выравнивание подразумевает, что последовательности гомологичны (схожи) по всей длине. В него включаются обе последовательности целиком. Однако при таком подходе не всегда хорошо определяются схожие участки, если их мало. Локальное выравнивание применяют, если последовательности содержат как гомологичные (например, из-за рекомбинации), так и неродственные участки. Но оно не всегда может попасть в интересующий участок, к тому же существует вероятность встречи случайного схожего участка. Для получения парного выравнивания используют методы динамического программирования (решение задачи путем её разбиения на несколько одинаковых подзадач, связанных рекуррентно). В программах для глобального выравнивания часто используют алгоритм Нидлмана-Вунша, а для локального — алгоритм Смита-Ватермана. Подробней о них можно прочитать по ссылкам.
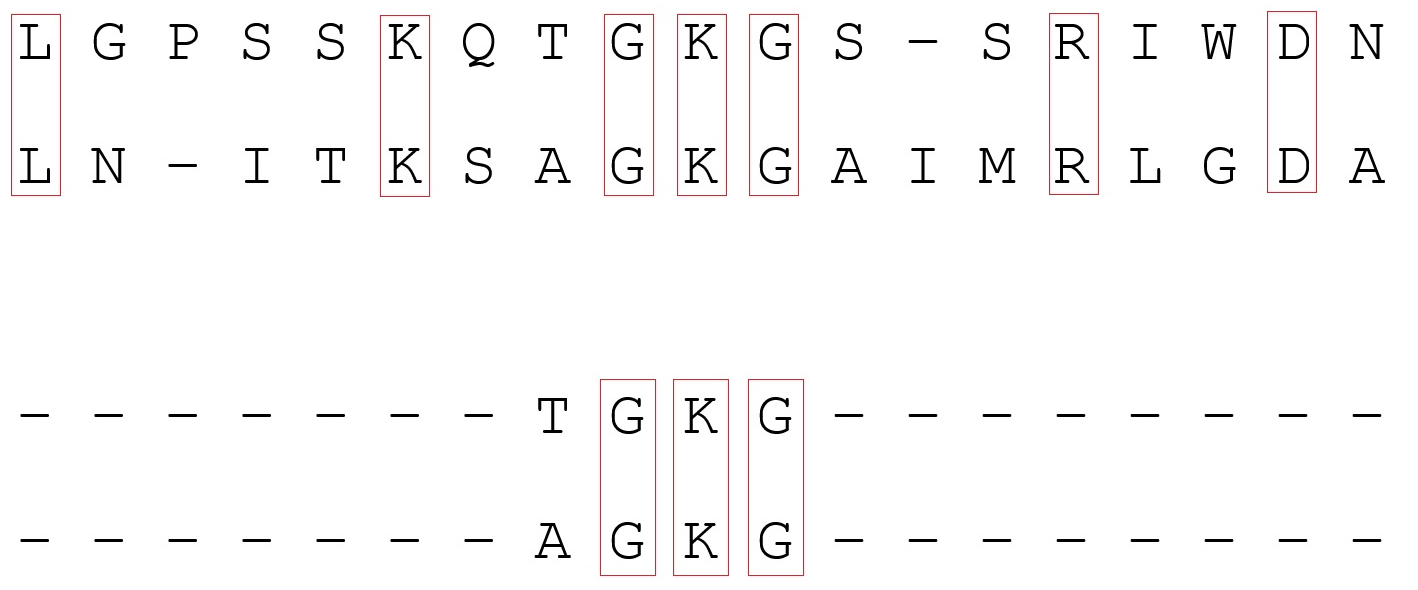
Пример выравнивания: вверху глобальное выравнивание, снизу — локальное. В первом случае выравнивание происходит по всей длине последовательностей, во втором — найдены некоторые гомологичные участки.
Как видим, биологическую задачу вполне можно свести к задаче из CS. При парном выравнивании с использованием упомянутых алгоритмов требуется порядка m*n дополнительной памяти (m, n — длины последовательностей), с чем легко справятся современные домашние компьютеры. Однако в биоинформатике существуют и более нетривиальные задачи, например множественное выравнивание (выравнивание нескольких последовательностей) для реконструкции филогенетических деревьев. Даже если сравнить 10 очень маленьких белков с длиной последовательности около 100 символов, то потребуется непозволительно много дополнительной памяти (размерность массива 100^10). Поэтому в таком случае выравнивание строится на базе различных эвристик.
Моделирование крупномасштабной структуры Вселенной
В отличие от биологии, физика идет бок о бок с Computer Science со времен появления первых ЭВМ. До создания первых компьютеров словом «computer» (вычислитель) называлась специальная должность — это были люди, выполнявшие на калькуляторах математические вычисления. Так в ходе Манхэттенского проекта физик Ричард Фейнман был управляющим целой команды «вычислителей», которые обрабатывали дифференциальные уравнения на арифмометрах.

«Вычислительная комната» Лётно-исследовательского центра им. Армстронга. США, 1949 год
На данный момент методы CS широко применяются в различных областях физики. Например, вычислительная физика изучает численные алгоритмы решения физических задачи, для которых количественная теория уже разработана. В ситуациях, когда непосредственное наблюдение объектов затруднено (такое часто бывает в астрономии), на помощь ученым приходит компьютерное моделирование. Именно таким случаем является изучение крупномасштабной структуры Вселенной: наблюдения далеких объектов затруднены из-за поглощения электромагнитного излучения в плоскости Млечного Пути, поэтому основным методом исследования стало моделирование.

Крупномасштабная структура Вселенной напоминает систему прожилок и волокон, разделенных пустотами
Одна из задач современной космологии — объяснение наблюдаемой картины многообразия галактик и их эволюции. На качественном уровне физические процессы, происходящие в галактиках, сейчас известны, поэтому усилия ученых направлены на получение количественных предсказаний. Это позволит ответить на ряд фундаментальных вопросов, например о свойствах темной материи. Но, прежде чем выделить наблюдаемые проявления темной материи, необходимо разобраться с поведением обычной материи. На огромных масштабах (несколько миллионов световых лет) обычная материя эффективно ведет себя так же, как и темная: она подвержена одной силе гравитации, про давление газа можно забыть. Это позволяет сравнительно просто моделировать эволюцию крупномасштабной структуры Вселенной (Численные методы, содержащие только темную или пылевидную материю и хорошо воспроизводящие крупномасштабную структуру распределения галактик, начали развиваться с 1980-х годов).
Моделирование темной материи происходит следующим образом. Виртуальный куб, имеющий размеры в сотни миллионов световых лет, почти равномерно заполняют пробными частицами — телами. С самого начала во Вселенной присутствовали малые неоднородности, из которых и возникла вся наблюдаемая структура, поэтому заполнение «почти равномерное». Затем частицы начинают «жить собственной жизнью» под действием силы тяготения: решается задача N тел. Вылетевшие за границу куба частицы переносятся на противоположную грань, силы тяготения также распространяется с переносом. Благодаря этому куб становится как бы бесконечным, как и Вселенная.

Приблизительные траектории трёх одинаковых тел, находившихся в вершинах неравнобедренного треугольника и обладавших нулевыми начальными скоростями
Одной из самых известных численных моделей такого типа — Millenium, имеющая размер куба более 1.5 млрд световых лет и около 10 млрд частиц. В последующие годы было выполнено несколько моделей большего объема: Horizon Run с размером стороны куба в 4 раза больше, чем Millenium, и Dark Sky с размером в 16 раз больше Millenium. Эти и подобные модели сыграли ключевую роль в проектах по проверке общепризнанной сейчас модели Лямбда-CDM (Вселенная, содержащая около 70% темной энергии, 25% темной материи и 5% обычной материи).

В верхнем ряду показано распределение галактик в модели Millenium: слева моделирование для скопления галактик, где их можно увидеть по отдельности; справа — для очень больших масштабов. Верхнее правое изображение представляет крупномасштабное распределение света во Вселенной. Для сравнения на изображениях в нижнем ряду приведены соответствующие распределения темной материи
При уменьшении масштабов возникают проблемы в соответствии наблюдений и численных моделей с одной темной материей. На более малых масштабах (масштабы распространения ударных волн от сверхновых) материю уже нельзя считать пылевидной. Необходимо учитывать гидродинамику, остывание и нагревание газа излучением и много чего еще. Для учета всех законов физики в моделировании делают некоторые упрощения: например, можно разбить модельный куб на решетку из ячеек (субрешёточная физика), и считать, что при достижении в ячейке некоторый плотности и температуры часть газа мгновенно превратится в звезду. К такому классу моделей относятся проекты EAGLE и illustris. Один из результатов этих проектов — воспроизведение соотношения Талли-Фишера между светимостью галактики скоростью вращения диска.
Лингвистика и машинное обучение: на один шаг ближе к разгадке 4000-летней тайны
Методы CS находят применения и в более неожиданных сферах, например в изучении древних языков и систем письма. Так исследование группы ученых под руководством Раджеша П. Н. Рао, профессора Вашингтонского университета, пролило свет на тайну письменности долины Инда.
Письменность Инда, использовавшаяся между 2600-1900 года до нашей эры на территории нынешнего Восточного Пакистана и северо-западной Индии, принадлежала цивилизации не менее сложной и загадочной, чем ее месопотамские и египетские современники. От нее осталось чрезвычайно мало письменных источников: археологи обнаружили лишь около 1500 уникальных надписей на фрагментах керамики, табличек и печатей. Длина самой длинной надписи составляет всего 27 знаков.

Надписи на печатях из долины Инда
В научной среде существовали разные гипотезы насчет «загадочных символов». Некоторые специалисты считали символы не более, чем просто «красивыми картинками». Так в 2004 году лингвист Стив Фармер опубликовал статью, в которой утверждалось, что письменность Инда является не чем иным, как политическими и религиозными символами. Его версия, хоть и являлась спорной, но все-таки нашла своих сторонников.
Раджеша П. Н. Рао, специалист по машинному обучению, читал о письменности Инда в старшей школе. Группа ученых под его руководством решила провести статистический анализ существующих достоверных документов. В ходе исследований при помощи цепей Маркова (одна из первых дисциплин, в которой цепи Маркова нашли практическое применения, стала текстология) сравнивалась условная энтропия символов из письменности Инда с энтропией лингвистических и нелингвистических последовательностей знаков. Условная энтропия — это энтропия для алфавита, для которого известны вероятности появления одной буквы после другой. Для сравнения было выбрано несколько систем. В лингвистические системы входили: шумерское логографическое письмо, старо-тамильская абугида, санскрит Риг-веды, современный английский (слова и буквы исследовались отдельно) и язык программирования Фортран. Нелингвистические системы разделили на две группы. К первой относились системы с жёстким порядком знаков (искусственный набор знаков №1), ко второй — системы с гибким порядком (белки бактерий, ДНК человека, искусственный набор знаков №2). В результате выяснилось, что протоиндийская письменность оказалась умеренно упорядоченной, как письменность разговорных языков: энтропия существующих документов сходна с энтропией шумерской и тамильской письменности.

Условная энтропия для различных лингвистических и нелингвистических систем
Такой результат опроверг гипотезы об орнаментальном использовании знаков. И хотя методы CS помогли подтвердить версию о том, что символы из долины Инда скорее всего являются системой письма, до расшифровки дело пока не дошло.
Заключение
Конечно, за бортом остались многие сферы, где методы CS находят применения. В одной статье просто невозможно раскрыть то, как современная наука полагается на компьютерные технологии. Однако, надеюсь, приведенные примеры показывают, насколько разными могут быть задачи, решаемые в том числе и методами CS.
Облачные серверы от Маклауд быстрые и безопасные.
Зарегистрируйтесь по ссылке выше или кликнув на баннер и получите 10% скидку на первый месяц аренды сервера любой конфигурации!



