После публикации серии статей про построение геологических моделей пришло время обсудить, скажем прямо, самое интересное — а насколько эти модели достоверны? Несомненно, все представленные ранее модели интересны и полезны — землетрясения, вулканы, золотые месторождения и другие. Теперь покажем, что они являются действительными геологическими моделями. На самом деле, мы уже все доказательства упоминали, но сегодня обсудим подробно. Теоретическая часть и история метода приведены в статье Методы компьютерного зрения для решения обратной задачи геофизики, на гитхабе опубликован Python ноутбук 3D Density Inversion by Circular Hough Transform (Focal Average) and Fractality Index с оценкой достоверности моделирования, и я даже написал техническую статью непосредственно об используемых там вычислительных методах Вычислительная геология и визуализация: пример Python 3 Jupyter Notebook, не касаясь геологического смысла выполняемых вычислений. Кроме того, в статье Геология XXI века как наука данных о Земле модель землетрясения заверена с помощью результатов спутниковой интерферометрии.
Вычислительные методы для оценки достоверности моделей
Поскольку мы используем вычислительные методы для построения геологических моделей, очевидным решением является использование также вычислительных методов для оценки достоверности получаемых моделей. Хорошо известные методы контроля сходимости при изменении масштаба модели и построения прямых моделей к обратным с последующим сравнением исходных данных и результатов прямого моделирования на обратной модели позволяют получить вычислительно корректный результат. В предлагаемом ноутбуке 3D Density Inversion by Circular Hough Transform (Focal Average) and Fractality Index выполнена именно такая последовательность действий: априори задана геологическая модель плотности, для которой посчитано распределение вертикальной компоненты гравитационного поля на поверхности (сила тяжести) — прямая модель, для этого распределения вычислена соответствующая модель геологической плотности — обратная модель, от построенной обратной модели снова вычислено распределение силы тяжести — прямая модель, после чего выполнено сравнение двух прямых моделей. Поскольку прямая модель определяется однозначно, то совпадение прямых моделей априори заданного и вычисленного распределений плотности гарантирует корректность обратной модели. Далее использован масштаб вычислений 1:4, то есть выполнено загрубление априори заданной модели в 4 раза, что ожидаемо снижает точность обратной модели — и тем не менее, мы все еще получаем высокую точность, как будет показано далее. Поскольку моделирование трехмерное, то уменьшение разрешения в 4 раза по каждой координате ускоряет вычисления в 64 раза (на два десятичных порядка), что очень существенно для больших моделей. Моделирование выполнено в безразмерных единицах, так что полученные результаты применимы для любых геологических масштабов.
Посмотрим на изображения априори заданной и восстановленной (обратной) моделей:

Здесь на обратной модели заметен краевой эффект в виде дополнительных темных поверхностей по краям. Этот эффект приводит к искажению визуализации обратной модели, поскольку отображаемые изоповерхности построены с фиксированным шагом в интервале от минимального до максимального значений плотности модели и при значимом изменении этих краевых значений изоповерхности обратной модели все более не совпадают с изоповерхностями априорной модели. Чтобы оценить величину и пространственное распределение краевого эффекта, сравним пространственные распределения силы тяжести (прямую модель) априори заданного распределения плотности и для обратной модели:

В третьей колонке выделено кольцо аномальных значений, связанных с краевым эффектом, причем эффект проявляется как вокруг всей модели (верхний график), так и вокруг каждого элемента плотностной модели (нижний график). При этом, внутри модели значение краевого эффекта мало и значения прямой модели совпадают с точностью 97.85% (Total Correlation на правом нижнем графике), а краевой эффект вокруг всей модели снижает корреляцию прямых моделей до 92.33% (Total Correlation на правом верхнем графике). Таким образом, необходимо строить обратную модель большего размера с возможностью удалить ее внешнюю часть с выраженным краевым эффектом. Внутренний краевой эффект незначителен и снижает точность прямой модели от обратной на 2.15% (100% — 97.85%), при этом краевой эффект уменьшается при использовании полосовой фильтрации, но не исчезает полностью. К примеру, после полосовой фильтрации в диапазоне 10-70 в безразмерных единицах моделирования внутренний краевой эффект уменьшается почти вдвое до 1.19% (100% — 98.81%):

Для оценки точности непосредственно обратной модели сравним ее профиль плотности по глубине с таким профилем для априори заданной модели путем вычисления линейной регрессии:
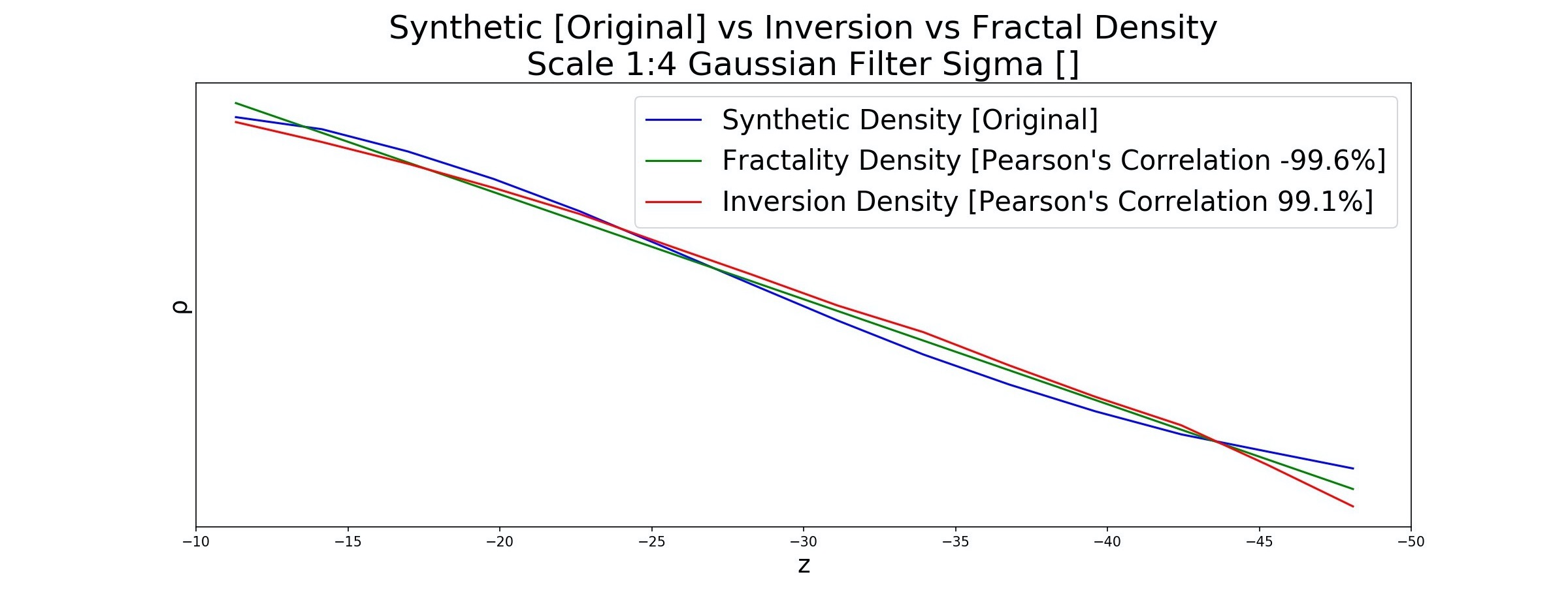
Здесь точность восстановления профиля плотности (Inversion Density) составляет 99.1% и зависит от параметров полосовой фильтрации.
Подводя итог, проведенное моделирование показывает возможность построения модели плотности геологической среды с высокой точностью 99% и выше при использовании полосовой фильтрации поля силы тяжести на поверхности. При более детальном масштабе вычисления (как указано выше, моделирование выполнено с загрублением в 4 раза) точность полученной модели еще увеличивается.
Спутниковая интерферометрия для оценки достоверности моделей
Этот метод легко доступен и понятен и обладает высокой детальностью. Спутниковая интерферограмма показывает вертикальные и горизонтальные смещения участков земной поверхности с субсантиметровой точностью почти в любой точке планеты (если там вообще возможно построить интерферограмму). Таким образом, задача валидации геологических моделей сводится к выделению геологических блоков и вычислению их трехмерного смещения между моментами времени до и после сейсмического события (достаточно слабого землетрясения на значительном удалении от рассматриваемой территории, что происходит постоянно и повсеместно) и сравнению этих смещений с полученными методом спутниковой интерферометрии. Поскольку интерферограмма представляет собой визуально понятную картину смещений, по наглядности именно этот метод превосходит все прочие. Вдобавок, такие интерферограммы открыто и регулярно публикуются для всех более-менее заметных сейсмических событий.
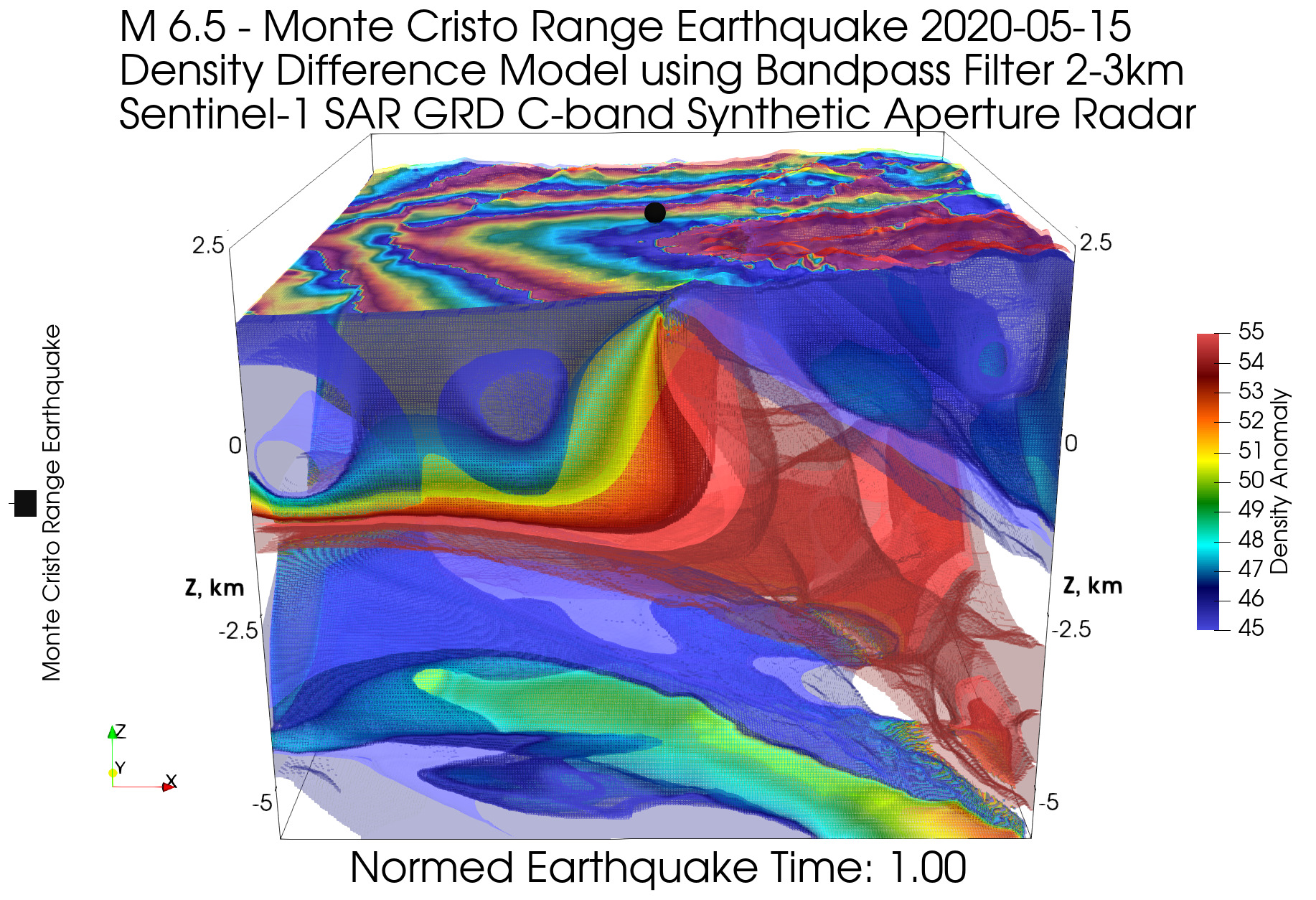
Приведем пример смещения геологических блоков для землетрясения (эпицентр показан черной точкой в центре модели на поверхности), модель которого мы уже рассматривали в статье Геология XXI века как наука данных о Земле:
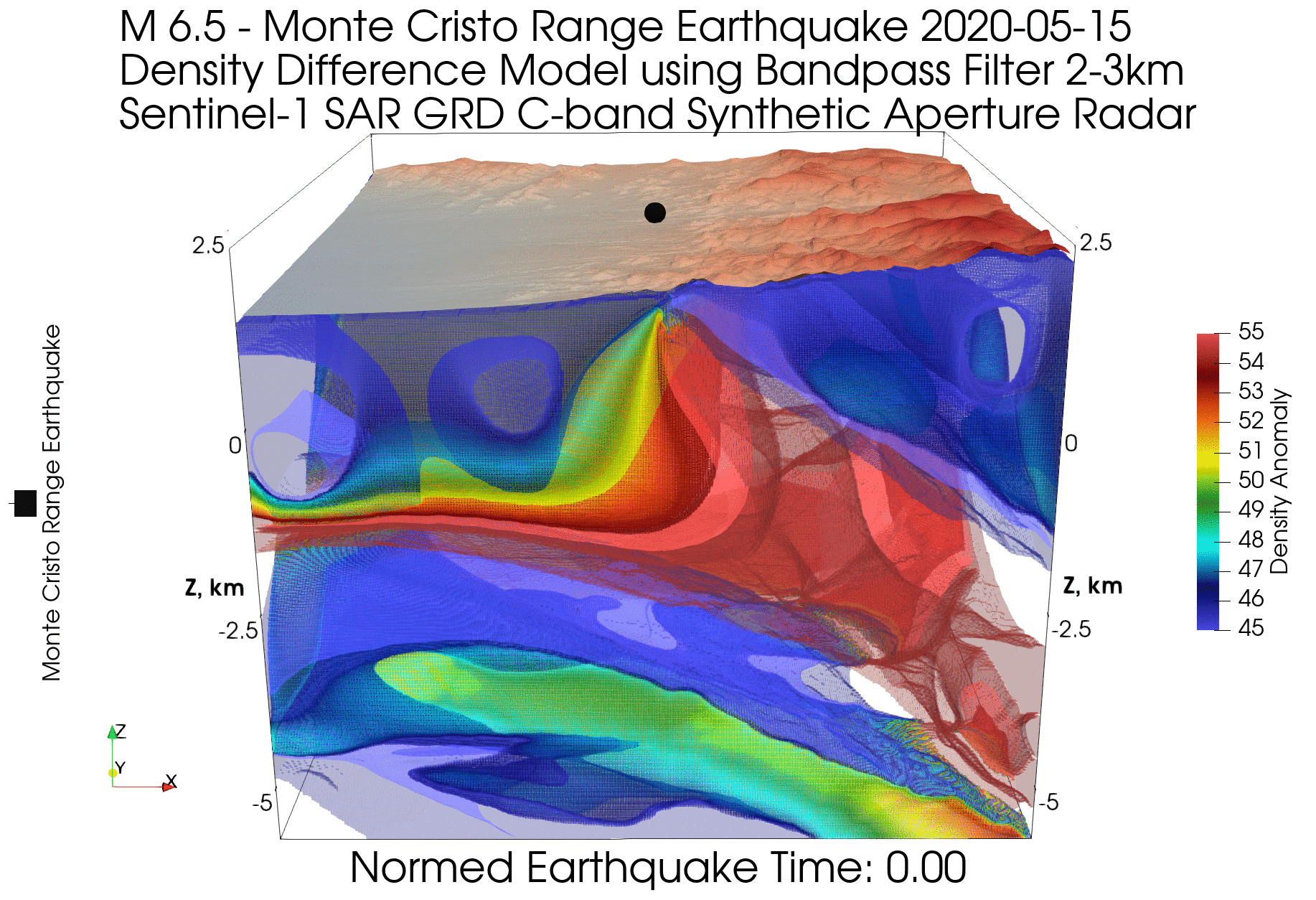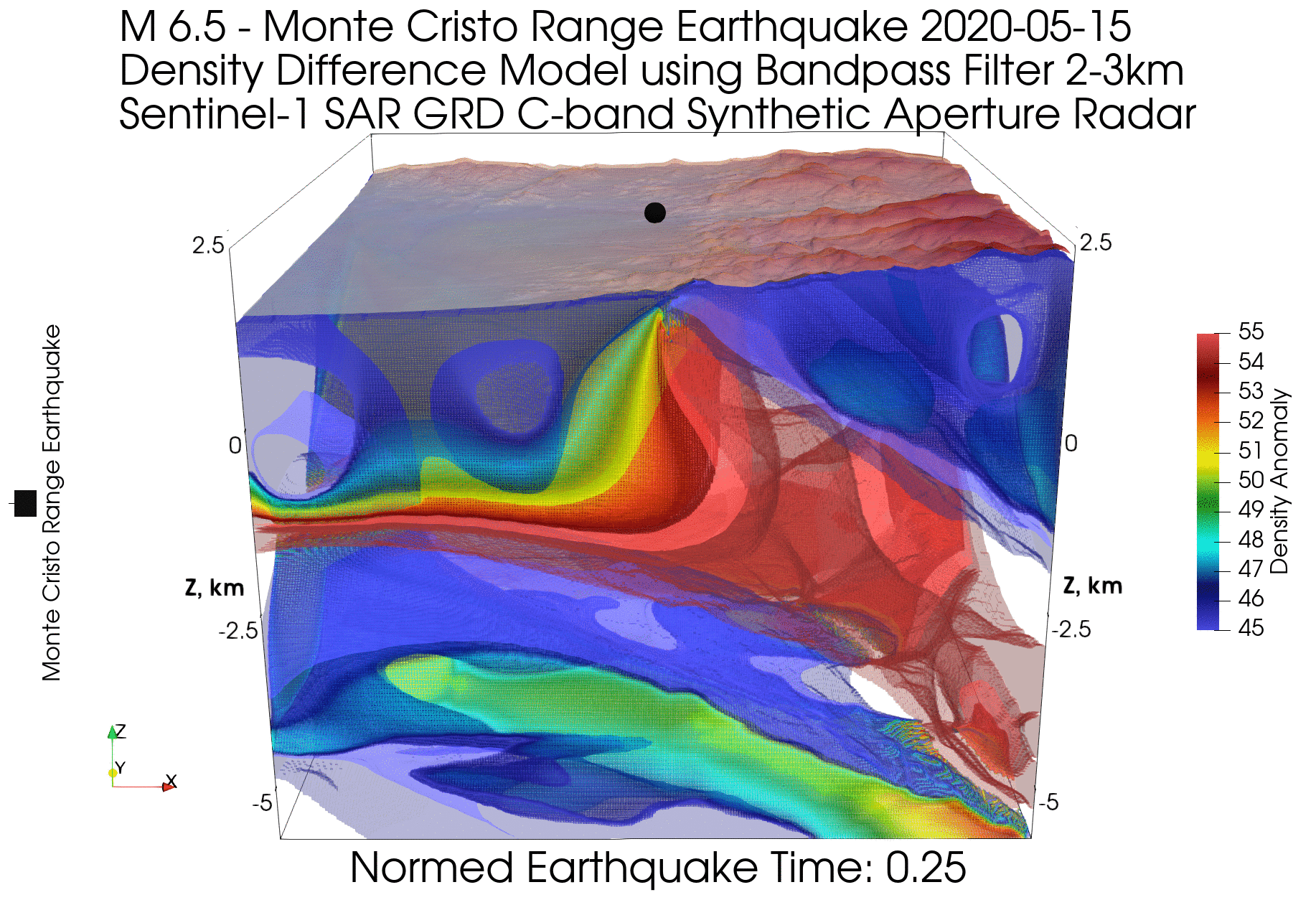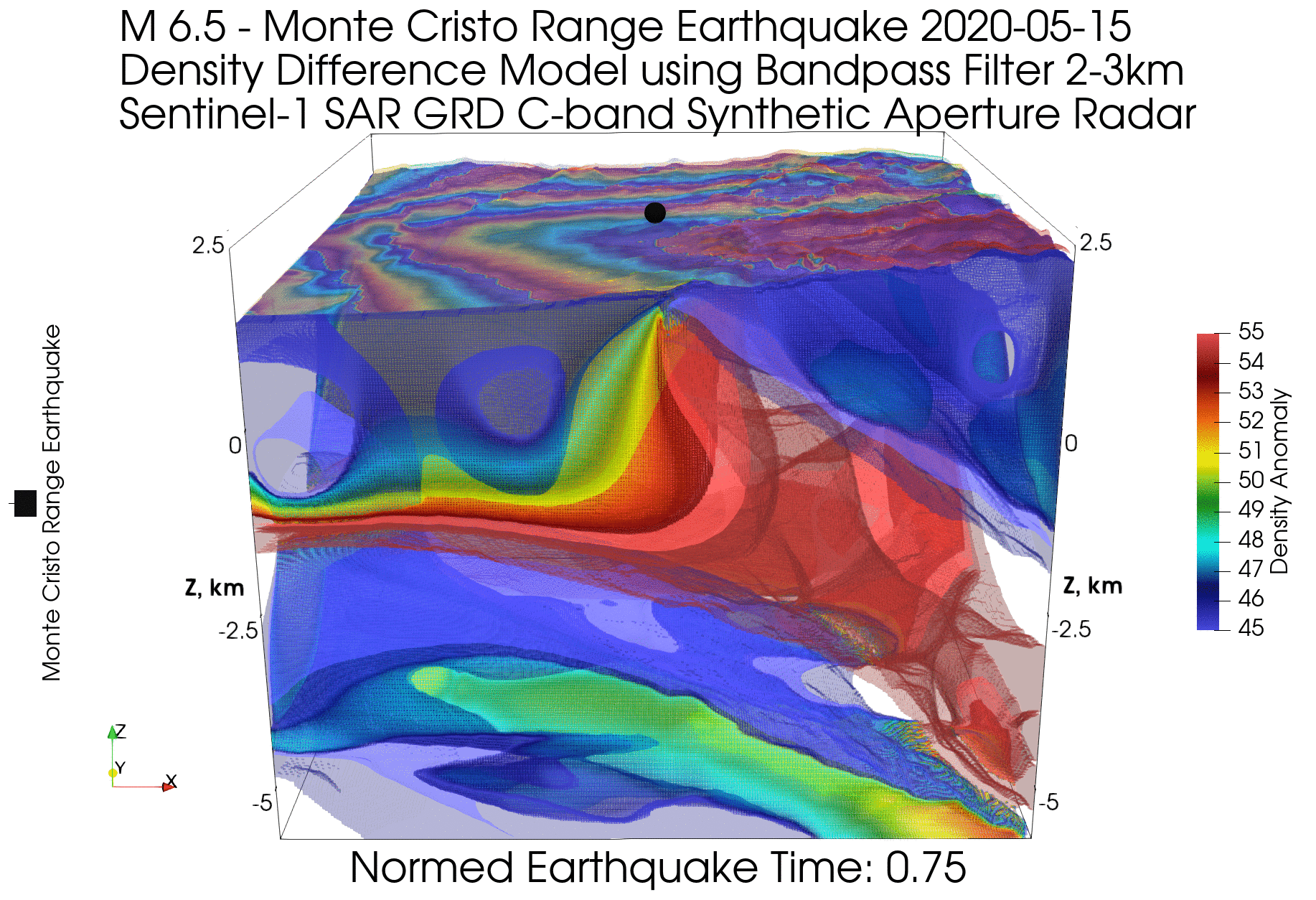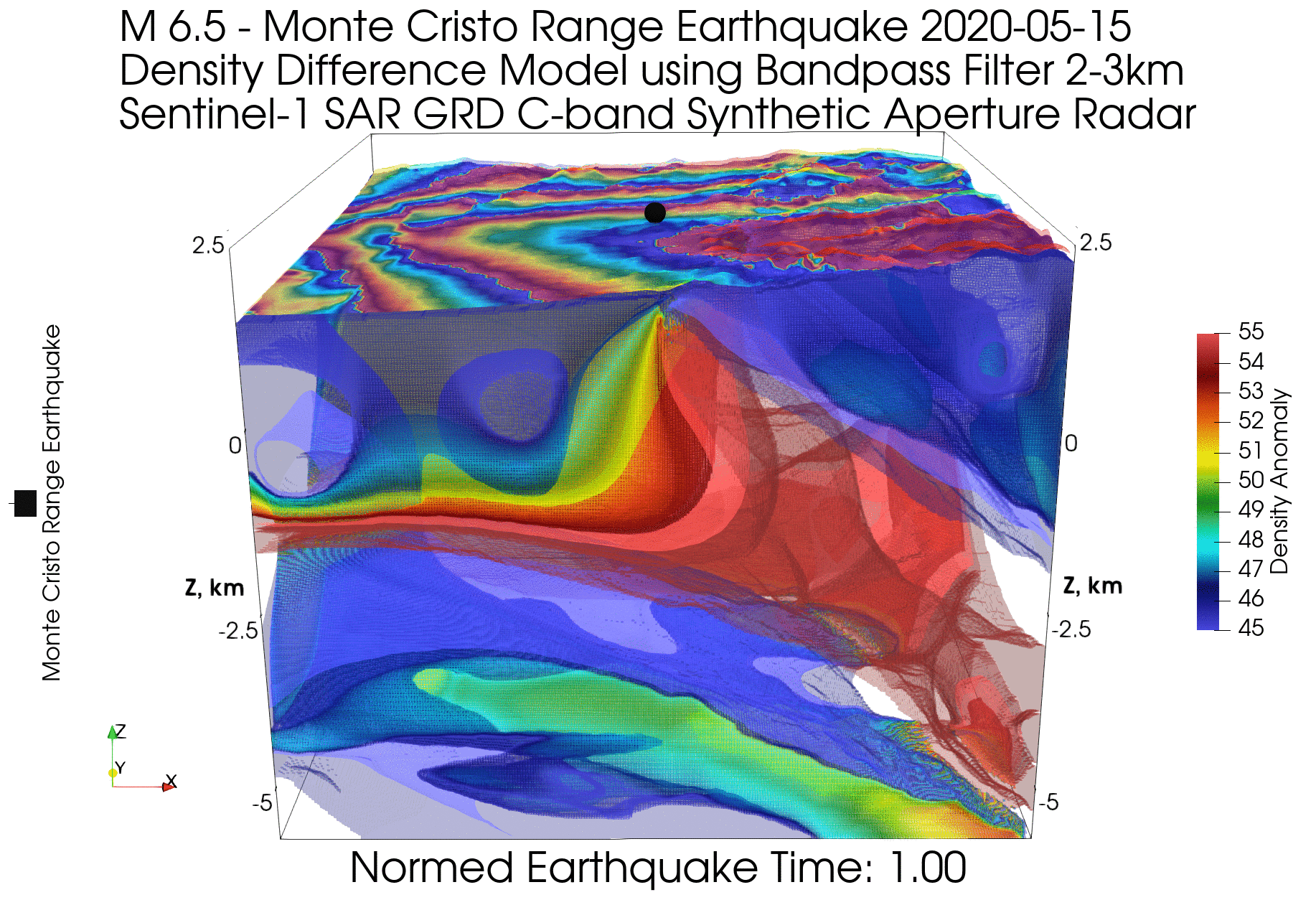
На модели видно, как опускается левый геологический блок и поднимается правый, при этом картинка фазовой интерферометрии на поверхности модели (в виде частей разноцветных колец) показывает расположение границ геологических блоков и центральной части опускающегося блока, которая имеет максимальную амплитуду вертикального сдвига. Вертикальный сдвиг можно визуально оценить по количеству колец (одно кольцо соответствует набегу фазы в 2π и расстоянию, равному длине волны используемого радара). Кроме того, можно воспользоваться готовыми картами вертикального и горизонтального смещений.
Посмотрим карты смещений для этого сейсмического события от Геологической службы США:

Таким образом, заверка моделей методом спутниковой интерферометрии требует построения дополнительной геологической модели, зато сами интерферограммы от общепризнанных доверенных источников доступны для визуального сравнения и анализа. Для подробного анализа можно построить и более детальные интерферограммы, наподобие показанной выше на поверхности модели.
Заключение
Как видим, мы действительно построили и рассматривали достоверные геологические модели и, более того, мы способны заверить их как вычислительными, так и геологическими методами. Мне встречались десятки аналогичных моделей и более десятка соответствующих диссертаций по геофизике, при этом их авторы не утруждают себя физическими основами метода и анализом вычислительных ограничений, что в итоге приводит к совокупности проблем: неоднозначности решения (отсутствие предварительной полосовой фильтрации), резким «выбросам» значений на границах модели (краевые эффекты), чрезвычайному загрублению получаемой модели (вычисление радиального градиента как разницы между кругами, а не кольцами, и вычисление по секторам, все это в попытке избавиться от не фильтрованного шума в исходных данных). Впрочем, это касается всех методов решения обратных задач без исключения — подготовка данных, аккуратность вычислений и валидация результатов имеют решающее значение.
Что же касается моделей машинного обучения на основе построенных геологических моделей, то для них оценки достоверности могут быть получены стандартными методами. Выполняя поиск параметров (grid search) мы уже оперируем оценкой точности, так что все сводится к правильной подготовке (и, при необходимости, разметке) исходных данных. Кроме того, повышая разрешение геологической модели мы увеличиваем и количество пикселов (пропорционально квадрату разрешения, то есть количеству пикселов на единицу площади), попадающих в размеченные контуры известных месторождений, что позволяет получить высокую точность даже при задании всего лишь нескольких небольших контуров.
В следующей статье мы поговорим про синтез сверхдетального рельефа и его валидацию для его использования в геомоделировании. Как будет показано, заявленные пространственное разрешение и вертикальная точность рельефа не значат (почти) ничего, так что, зачастую, нельзя просто купить качественный детальный рельеф, подходящий для целей геомоделирования, но можно построить его по открытым данным.


