Значимость естественных наук в XIX веке претерпевает положительную обратную связь: достижения исследователей несут вклад в промышленную революцию, а общественный уклад задает вектор дальнейших изысканий. Молекулярная теория, химия, гидро- и электродинамика находят применение не только на фабриках и в военной технике, но и в создании более точного оборудования. Помимо попыток объяснения микромира потоками эфира, все большую обособленность обретает атомистическая модель древних. Во многом эти модели конфликтовали, но несмотря на предрасположенность научного сообщества того времени к хорошо проработанному аппарату гидродинамики, возникает необходимость пересмотреть многие укоренившиеся взгляды – этого требовали результаты экспериментов.
Результаты опытов по рассеянию нужно было обосновать теоретически, так что для начала XX века характерна чехарда моделей атома. Возможно, атомы бывают положительные и отрицательные, или они представлены вихрями эфира, или же слагаются из водорода, а то и из нулевого элемента. Эти предположения математически обосновывали, публиковали, а потом, на собраниях сообществ и клубов, достопочтенные сэры гневно шипя сквозь кустистые бороды разносили их в пыль. Романтика механистичного мира на фоне меняющейся парадигмы.

Немного пофантазируем. На дворе апрель 1911 года, вы работаете в британском научном издательстве, которому уже больше ста лет. Проверив крепления огромной типографской машины, вы вытираете выпачканные руки о вчерашнюю газету: там все еще мусолят судебный процесс над латышскими анархистами и делают прогнозы касательно грядущего суперкубка по футболу, до которого осталось ждать менее полугода. Бульварная пресса вас не интересует – в свободное время вы частенько перечитываете черновики и корректурные оттиски готовящихся журналов, тем самым обеспечив себя доступом к периферии науки.
Вот очередная статья готовящаяся к выходу. Сэр Резерфорд обобщает результаты своих экспериментов проведенных два года назад и предлагает новую модель атома. Вы бежите в каморку с инструментами к своему импровизированному архиву. Ага, вот она… Отбракованный вариант статьи Дж. Томсона семилетней давности. Он решил, что атом удобней представить как положительно заряженную сферу с вкраплениями электронов, подобными кровяным тельцам. Вы поднимаете глаза на лежащий на столе сухарь – не утверждаете ли, сэр, что электроны сидят внутри атома, как изюм в пудинге?
И вновь возвращаетесь к новой статье – формулы и таблицы неинтересны, а вот концовку перечитываете несколько раз. Выходит, ядро куда меньше атома, и оно имеет положительный заряд, а он пропорционален массе. Пропорционален… Пудинг неумолимо сжимается в комок мякиша освобождая изюминки-электроны. Они начинают порхать вокруг, как мошки не решающиеся сесть. Или… Как спутники вокруг Сатурна! Или даже, как планеты вокруг Солнца! На минуту перехватывает дух…
На самом деле, подобную планетарную модель предложил еще в 1904 году Хантаро Нагаока, и вполне возможно, что такие предложения были и раньше и в больших количествах, просто не успели отпечататься в окаменелостях истории.
Классика
Вооружимся формулами классической физики и выясним, что не так с атомом-планетной системой. Рассмотрим атом водорода — вокруг положительно заряженного протона по круговой орбите летает шарик-электрон. Их взаимодействие обуславливает сила Кулона, а движение по окружности подразумевает наличие центростремительного ускорения. Запишем второй закон Ньютона и выразим квадрат скорости электрона для дальнейших подстановок:
где k константа связанная с диэлектрической проницаемостью. Полная энергия E будет слагаться из кинетической K и потенциальной U:
В предыдущей статье мы выяснили, что во время движения с ускорением, заряженная частица испускает электромагнитные волны теряя при этом энергию. Там же была получена формула Лармора, позволяющая оценить потерянную энергию. Для нашего электрона картина силовых линий возмущенного поля выглядит как-то так
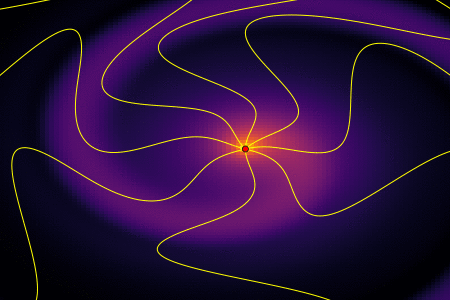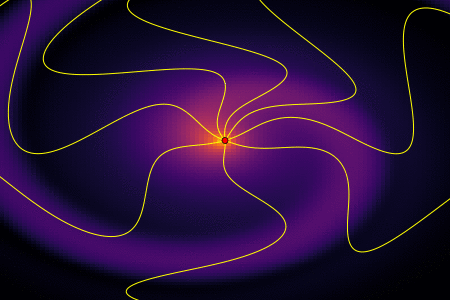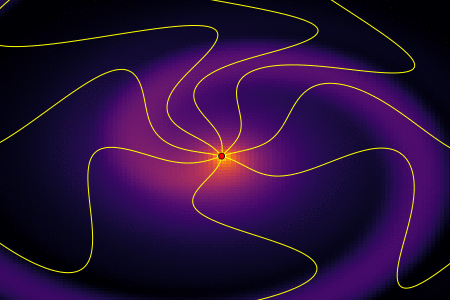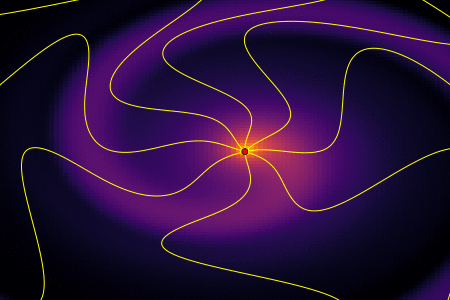
Двигаясь по окружности, электрон постоянно излучает. За один оборот периодом T теряется количество энергии:
С другой стороны, посмотрим на формулу полной энергии. Е будет изменяться за счет медленного изменения радиуса орбиты электрона:
Приравниваем к предыдущей формуле и получим выражение для скорости изменения радиуса орбиты
Здесь мы ввели радиус электрона rₑ. После подстановки всех констант должно выйти, что он раза в три больше протона. Спокойствие, только спокойствие! Величина фиктивная, а в квантмехе электрон все равно считается точечным, но более-менее сферическим. Собственно, теперь мы можем оценить время падения электрона
где a₀ – боровский радиус, который можно получить из фундаментальных постоянных. Все константы известны, так что подстановка дает время около 16 пикосекунд или около 0.02 наносекунды. Процессор моего ноутбука не успеет сделать ни одной операции, в то время как электроны основного состояния атомов водорода, навернув по две сотни тысяч кругов, посыпятся на свои протоны. Учет релятивистских поправок только усугубит ситуацию — падение произойдет быстрее.
Проблему пробовали решить множеством способов разной степени костыльности: некулоновское взаимодействие, неевклидовы геометрии, причудливые траектории. Наиболее успешным был вариант предложенный Нильсом Бором. Он постулировал квантование момента импульса для электрона (интересующихся выкладками пошлем на researchgate). То есть момент импульса меняется рывками, а значит есть только ряд разрешенных орбит, между которыми электрону быть нельзя. В качестве лирического отступления предлагаю посмотреть ламповый советский ролик по теме.
В целом, такое решение хорошо согласовалось с результатами экспериментов и помогло объяснить некоторые явления в спектроскопии (ограничиваясь атомом водорода). Но истинным теоретикам требовались уравнения, из которых эти орбиты выходили бы как следствие, а не постулаты. Нильс Бор, будучи больше философом, в дальнейшем начал активно продвигать вопрос о роли познания и сознания, а его революционные идеи (в частности, касательно роли наблюдаемых величин) вдохновили тогда еще молодого Вернера Гейзенберга и Вольфганга Паули на создание новой физики. И совместными силами они в дальнейшем сформируют и распространят раннюю Копенгагенскую интерпретацию. Довольно интересно воспринимать парадигму не как строго формализованную, последовательную эволюцию теорий, а с исторических и психологических позиций — через биографии культовых, но все же эмоциональных и склонных к профдеформации и культурным веяниям личностей. А ведь все это происходило на фоне зарождающегося нью-эйдж. Забавно было обнаружить, что Бор тоже в некотором роде фанат учителя Цзы.
Материалы для любознательных:
-
Примеры классических моделей пытающихся спасти атом: пара старых и пара новых.
-
Детальные выкладки для модели Бора.
-
Увлекательная и романтичная история создания квантовой механики.
-
Вывод обобщенного лоренц-ковариантного аналога формулы Лармора.
-
Движение заряда с учетом магнитных полей смотрим в книге Classical Electromagnetic Radiation Mark A. Heald, Jerry B. Marion
-
Юпитерские блокноты с кодом для возмущений ЭП и атома Резерфорда, а также для орбит атома водорода.
-
Бонус: мнимые электроны и масса электрона предсказанная из его структуры! (Электромагнитное происхождение массы и электрон состоящий из триолетов — этой бомбе следовало бы посвятить отдельную статью)
Квантовый ответ
Каждый школьник знает, что атом Бора — это не атом бора, а атом водорода
П. Л. Капица
Практика показала, что квантование излучаемой энергии и орбит — довольно эффективный подход, который со временем оказался нечтом большим, чем просто математический трюк. Эрвин Шредингер, вдохновившись корпускулярно-волновым дуализмом де Бройля, получил релятивистское уравнение, которое затем проверил на атоме водорода. Результаты не совпали с экспериментальными данными, поэтому уравнение назвали уравнением Клейна-Гордона. А вот нерелятивистский вариант сработал безотказно.
Это так называемая задача на собственные значения, а Эрвин Рудольфович как раз был хорош в подобных вопросах. Для водорода, уравнение легко решается аналитически. Результатом будет набор собственных функций и энергий, где индексы это итераторы (квантовые числа)
подробности
Итак, у нас есть набор маленьких волновых функций, каждая из которых соответствует определенному состоянию электрона. Визуализуем несколько энергетических уровней
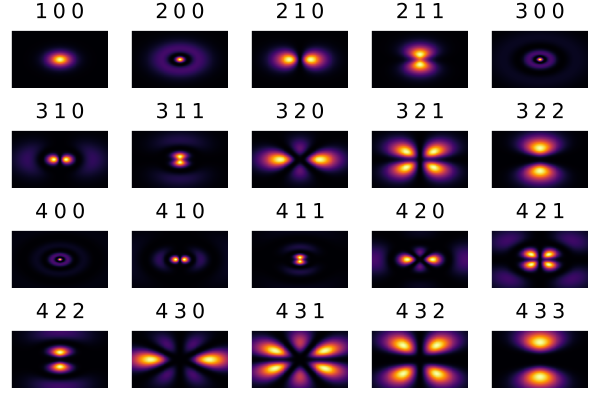
Ядро находится в центре каждого изображения, а температура цвета показывает где гуще облачко (или где чаще находится точечный электрон). Каждое состояние электрона определяет тройка квантовых чисел: первое число связано с энергией электрона, другие два – с угловым и магнитным моментами.
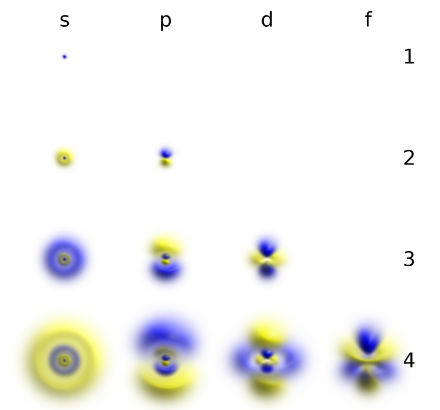
Атомные орбитали водорода – каждому состоянию электрона соответствует своя картинка. Картинки воспринимают в зависимости от того, как кто трактует понятие «волновая функция». Либо это лишь математические объекты – жильцы конфигурационного пространства, либо смотрим на электрон, как на отрицательно заряженное облако вокруг ядра, мгновенно меняющее свою форму после поглощения кванта энергии. Строго говоря, по настоящему стационарное только 1S-состояние (ѱ₁₀₀), потому как из остальных электрон вываливается после спонтанного испускания энергии. Остановимся на нем поподробней.
Плотность вероятности обнаружения электрона в определенной области для основного состояния имеет сферическую симметрию. Так что удобней будет представить это дело как радиальную зависимость вероятности обнаружения электрона на определенном расстоянии от центра ядра:

Здесь по оси абсцисс расстояние измеряется в атомных единицах. То есть, наш 1S-электрон по завету Нильса Бора чаще всего обитается на расстоянии в пол ангстрема (50 миллиардных миллиметра) от центра ядра. Ядро атома (в нашем случае один протон) имеет ненулевой размер, так что есть ненулевая вероятность пребывания электрона внутри ядра.
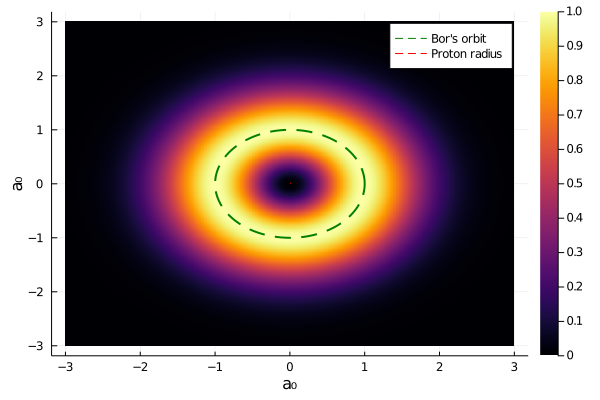
Так-то, ядру безразлично, что электрон может тусоваться поблизости, а то и залазить в самую душу – расстояние между уровнями внутренней энергии ядра гораздо больше, чем то, что творится в орбитальной энергетике электрона. Другой вопрос, если речь идет не о водороде, а о более массивном элементе, где больше нуклонов, а значит, больше радиус ядра и пронырливей электроны нижних уровней. Бывает, что в процессе перехода ядра в более энергетически выгодное состояние, оно захватывает электрон с ближайшей орбитали. Тогда один из протонов становится нейтроном, попутно выплюнув нейтрино. А атом тогда сдвигается на одну позицию в таблице Менделеева (ага, декрементирует).
Это явление называется электронным захватом. Для тяжелых атомов это довольно распространенное явление, и уже давно идут споры, дескать, могут ли вообще существовать элементы далее 137-го. Самое грандиозное проявление этого эффекта происходит в недрах звезд, где из-за высоких плотностей вещества ядра охотно пожирают электроны, множа нейтроны и испуская потоки нейтрино, что делает массивную звезду неустойчивой и определяет ее дальнейшее перерождение.
Материалы для заинтересовавшихся темой:
-
Хабровская статья (с ошибками)
Волна-пилот
Историю бомовской механики (теории волны-пилота, интерпретации де Бройля-Бома) мы уже обсуждали, погодя затронув сопутствующий формализм. В двух словах, это каузальный подход к квантовой механике, где частицы – это действительно частицы, но их поведением управляет мир волновых функций, играющих роль нелокальных скрытых переменных. Здесь, второй закон Ньютона для корпускул имеет вид:
То есть, помимо некоего классического потенциала, на частицу действует еще и квантовый потенциал. В рамках формализма, можно выразить импульс (скорость) частицы через фазу волновой функции:
И раз уж пошло такое веселье, то было бы здорово посмотреть на атом водорода с электроном влекомым волнами вероятности. Для этого выведем фазу его волновой функции и получим импульс электрона:
Компонента S₀ не зависит от времени, а скорость частицы определяется мнимой частью стационарной волновой функции. И казалось бы, знай себе подставляй волновые функции из решения уравнения Шредингера да рисуй орбиты, но есть один забавный момент. Для всех собственных состояний с m = 0 волновая функция реальна, потому что полиномы Лагерра и Лежандра всех степеней и порядков реальны, а за мнимую компоненту отвечают сферические гармоники Y. Тогда, фаза S₀ равна нулю как и скорость электрона. Очень интересный результат. Выходит в основном состоянии атома водорода электрон неподвижен!
Дэвид Бом знал об этом, когда впервые опубликовал свою теорию и использовал этот результат в качестве доказательства правильности предложенного подхода. По его словам, это дало объяснение тому, почему электрон в атоме водорода не пикирует прямиком в ядро – квантовый потенциал, действующий на электрон, таков, что полностью уравновешивает электрическое притяжение, оказываемое ядром, тем самым отменяет движение электрона. Таким образом, электрон висит себе в атоме как гроб Магомета, без излучения и магнитного момента.
Выходит палка о двух концах: на одной стороне находится положительное ядро, а на другой – отрицательный электрон, так что у такой системы должен быть ярко выраженный дипольный момент. Да и если рассматривать остальные собственные функции, у которых все же есть магнитный момент, то получится движение электрона с постоянной скоростью – почему же он тогда не излучает как в модели Резерфорда?
В механике Бома частицы сами по себе не обладают такими свойствами, как заряд или спин. Они только входят в качестве параметров в гамильтониан в уравнении Шредингера, решение которого порождает траектории. Бомовские частицы пассивны в том смысле, что они не влияют на эволюцию волновой функции во времени. При некоторых условиях, траектории будут приближаться к классическим, осуществляя предельный переход к привычной нам механике. Но в более общем случае динамика, вытекающая из эволюционного уравнения, может быть в высшей степени неклассической.
Отвечая на вопрос, как будет вести себя система находясь в изолированном состоянии, следует разобраться, можем ли мы вообще говорить о свойствах «изолированной» материи. Познание происходит только через взаимодействие, измерение, а это динамический процесс, который может влиять на скорость частицы. Однако более важно то, что это процесс, в котором состояние системы влияет на компоненты скорости, присущие сложному состоянию измерительного прибора, что потом выливается в понятные нам цифры на дисплее. А пока электрон находится в покое, он никогда не будет найден в покое.
Если же обратиться к вопросу о том, почему атом не испускает электромагнитное излучение, то, по-видимому, следует принять во внимание все электромагнитное поле, а также обобщить формулу Лармора.
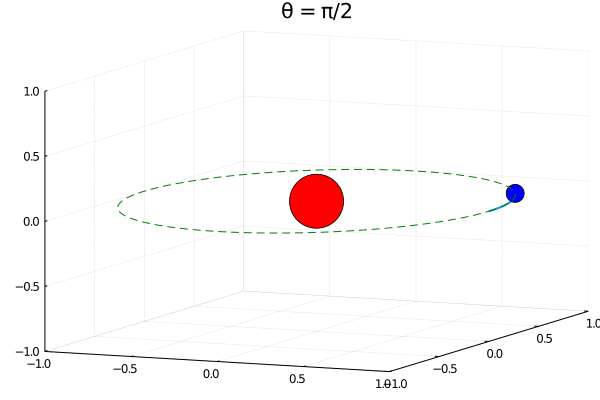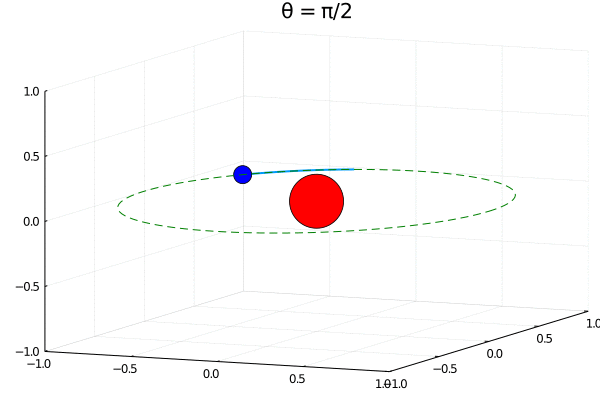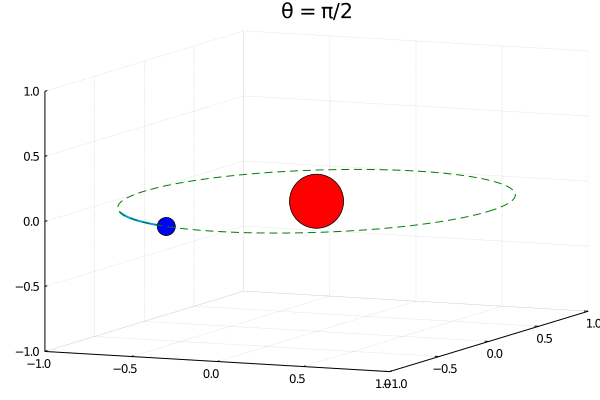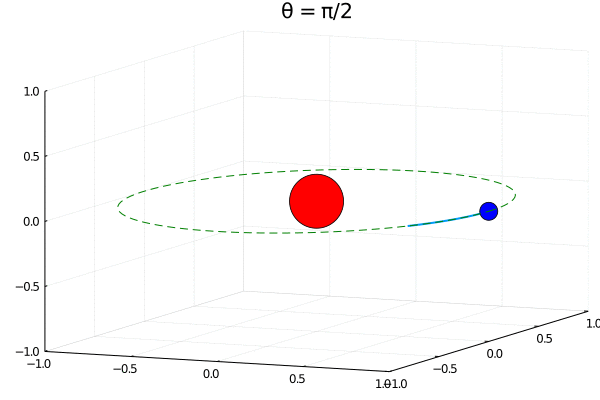
С другой стороны, мы отталкивались от нерелятивистского уравнения Шредингера. А что если начинать рассуждения с уравнений Паули и Дирака? Для более общих моделей волна-пилот тоже работает, и учет спина отражается на формуле нахождения скорости
Теперь, из-за вклада слагаемого зависящего от спина даже в основном S-состоянии должно наблюдаться движение, закон которого можно получить аналитически:
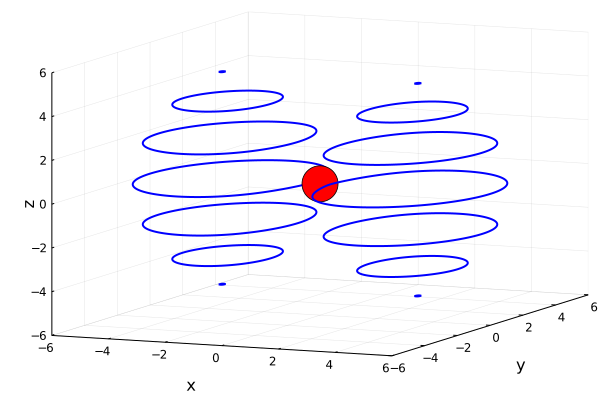
Мы выбрали спин сонаправленным оси Z. Электрон тогда движется в плоскостях к которым эта ось перпендикулярна. Таким образом, мы получаем все ту же сферическую плотность, но с ярко выраженным орбитальным движением электрона, зависящим от начального полярного угла и радиуса орбиты.
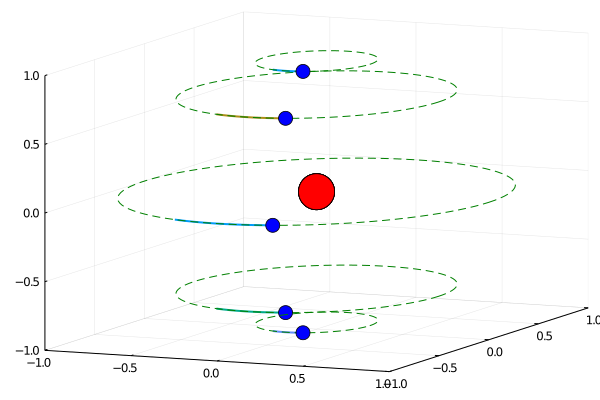
В состояниях с квантовым числом m не равным нулю, оно влияет на скорость, а также говорит, что на одну квантовую орбиту помещается ровно |m| длин волн де Бройля, что можно сравнить с квантованием Бора-Зоммерфельда. Тот факт, что радиус орбиты выбирается свободно, означает, в частности , что он не зависит от энергии или числа m. Поэтому картина несколько отличается от примитивной модели Бора, в которой электрон движется по кругу в экваториальной плоскости, а радиус является функцией m. У нас квантование проявляется скорее в величине скорости частицы.
Интересующимся серьезными выкладками посоветуем изучить диссертацию Кэролайн Колин. Там, помимо анализа орбит для стационарных состояний, предлагается исследование переходов, а также разбор критики траекторного подхода. В конце можно ознакомиться с направлениями дальнейших исследований и может даже выбрать что-либо для себя – Кэролайн теперь занимается эпидемиологией и борется с ковидом.
Разумеется, применение бомовской механики не ограничивается изолированным атомом водорода. Так, например, можно рассмотреть водородоподобные атомы в вакууме (квантовом), что позволяет нащупать всяческие тонкие эффекты типа Лэмбовского сдвига. Наши игрушечные системы выглядели до жути симметричными и простыми, но все же, хаотическое поведение траекторий имеет место быть и задает свой вектор исследований.
После игр с водородом непременно захочется глянуть на более сложные системы. Например, на атом гелия, молекулярные орбитали (+в связке с DFT), молекулярную динамику, туннелирование через пептидные цепочки, аттосекундные процессы, запутанность многих частиц, электромагнетизм, магнитные поля маленьких молекул, терагерцевую электронику (+книга +симулятор), квантовые вычисления, теорию поля, и замахи на релятивистское пространство-время (раз, два, +обзор).
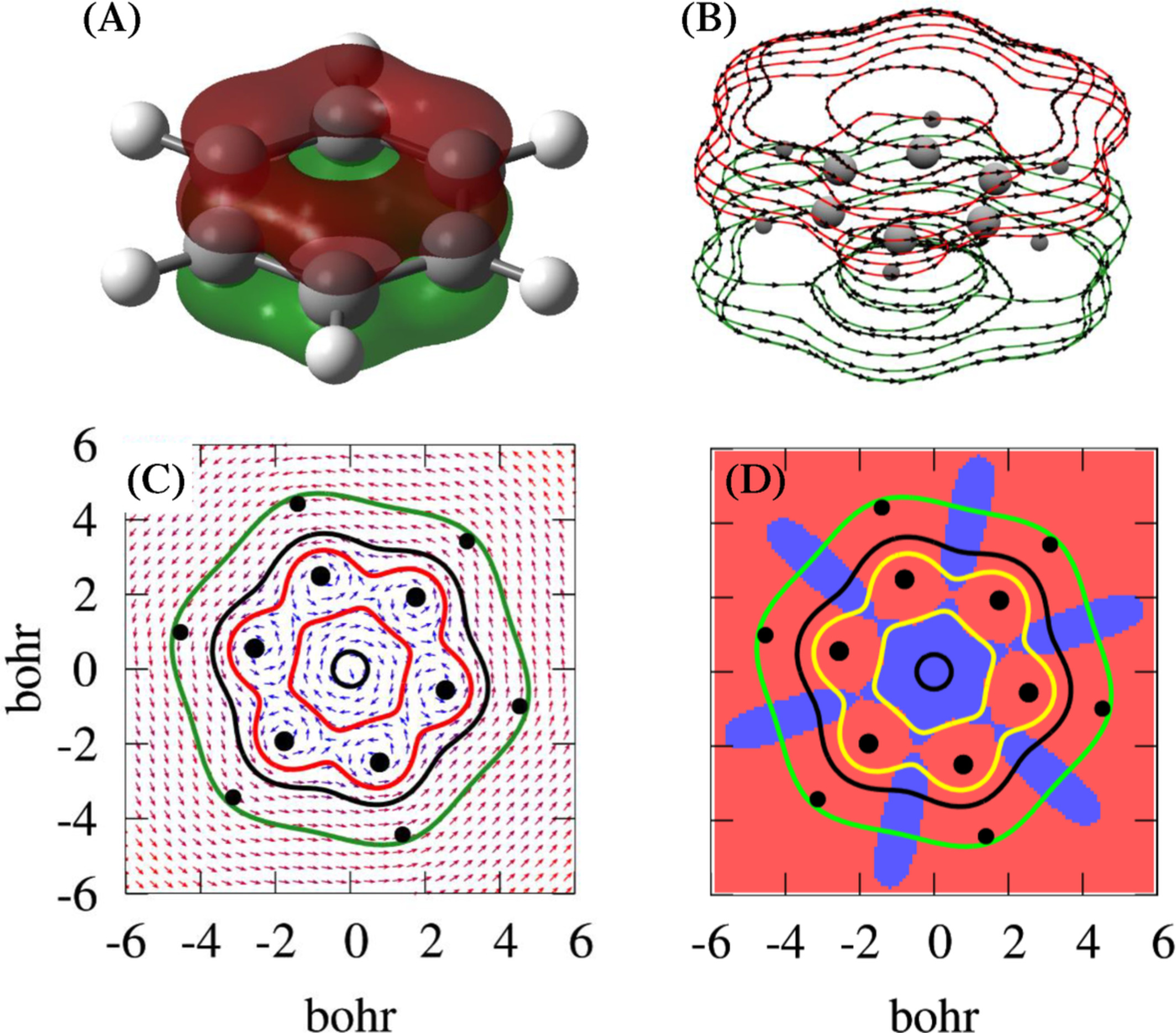
В то время как ортодоксальная интерпретация предполагает, что вероятность носит фундаментальный характер, теория де Бройля-Бома детерминистична, и вероятность проявляется только как выражение невежества, превращая фундаментальный детерминизм в прогностический индетерминизм. Поэтому дальнейшие изыскания должны проходить с оглядкой на проблемы детерминизма (раз, два, три ), локальности (раз, два) и нелинейности.
В целом, просматривая литературу по теории волны-пилота можно выделить три направления:
-
Квантовая гидродинамика. Исторически, все же правильнее связывать с Эрвином Маделунгом и Луи де Бройлем, а также большой вклад был внесен Шредингером, Лондоном и Ландау. В рамках подхода, эволюцию квантовых состояний рассматривают как гидродинамику невязкой идеальной жидкости, а математика уравнения Шредингера – это просто математика уравнения диффузии с мнимой константой скорости. Интерпретационные вопросы, как правило, не поднимаются, а квантовый потенциал воспринимается просто как побочный продукт.
-
Квантовые траектории. Само по себе это довольно обширное направление в физике твердого тела и конденсированных сред, так что неудивительно, что бомовская механика сюда незаметно затесалась. К математике из предыдущего направления добавляются частицы и больше внимания уделяется квантовому потенциалу. Зачастую частицы носят чисто иллюстративную роль, как крупинки красителя, помогающие визуализировать поведение волн и вихрей в жидкости. Либо же, работает синтетический подход, направленный на вычисление квантово-механических величин «на лету» путем прямого синтеза бомовских траекторий без необходимости предварительного определения волновой функции. В этом случае уравнения движения для траекторий интегрируются вместе с квантовым уравнением Гамильтона-Якоби (которое управляет динамикой траектории) и уравнением непрерывности (которое управляет динамикой «ансамбля»). Подробней смотрим в обзоре и книжках:
-
Интерпретация. Здесь уже поднимается философия и метафизика, противопоставление с копенгагенской интерпретацией, трактовка экспериментов, критика и дискуссии. На этой дороженьке можно увязнуть надолго, так что ограничимся лекциями Кембриджского университета.
До сих пор квантовый мир приводил и продолжает приводить нас в замешательство, бросая вызов нашей повседневной интуиции и нашим наисложнейшим математическим моделям, поэтому любой инструмент для его изучения всегда должен приветствоваться, а не запрещаться. Даже простой школьный вопрос способен увести на фундаментальный уровень, где царит лишь экзистенциальный ужас перед той сложностью взаимосвязей, в которых проявляется окружающий мир. Так что, наша задача состоит в том, чтобы не бояться задавать эти вопросы и, сохранив детскую любознательность и открытость новым идеям, прокладывать свою траекторию по волнам бушующей вероятности.


