Последнее время из каждого утюга слышатся хвалебные высказывания о многомировой интерпретации квантовой механики и негативные в сторону Копенгагенской. Вот, например, относительно недавняя статья на Хабре. Приверженцев идей отцов-основателей (Нильса Бора, Вернера Гейзенберга, Пола Дирака, Вольфганга Паули) теперь считают динозаврами, отказывающимися принять современную (1957 год) многомировую трактовку.
Действительно, на первый взгляд многомировая интерпретация кажется логичной и у непосвященного знакомство с ней обычно вызывает недоумение типа «Как же можно с этим спорить? Все же очевидно! Почему ученые так держатся за Копенгагенскую?». Но, как и всегда, дьявол кроется в деталях. Отцы-основатели в отличие от алкоголика Хью Эверетта не были дураками.
Копенгагенская интерпретация

Квантовая механика представляет собой фреймворк, набор постулатов (аксиом). Разные источники приводят различное их количество. В некоторых случаях одни постулаты можно вывести из других. Но тогда изложение и без того сложного материала еще более усложняется, поэтому формулируют обычно 5-6 штук.
Этот фреймворк можно применять к различным ситуациям и разрабатывать на его основе более детальные теории: нерелятивистскую квантовую механику частицы, релятивистскую квантовую механику, квантовую теорию поля (электромагнитного, сильного, слабого, Хиггса и пр.), теорию струн, физику твердого тела и еще много чего.
Большинство постулатов связывают абстрактные математические структуры с физикой, например:
Наблюдаемым величинам соответствуют эрмитовы операторы.
или
При измерении величины, соответствующей данному оператору, возможно получить лишь одно из собственных значений данного оператора.
или
Состояние системы (максимально возможная информация о системе), описывается вектором в Гильбертовом пространстве, называемым вектором состояния.
Эти абстрактные постулаты не с потолка взяты, а из критерия соответствия предсказаний теории экспериментальным данным. Для дальнейшей дискуссии нам понадобятся следующие два постулата. Постулат об измерении:
При измерении величины, соответствующей данному оператору, вектор состояния коллапсирует в один из собственных векторов данного оператора, причем в тот, что соответствует измеренному собственному значению.
и правило Борна:
Вероятность того, что при измерении мы получим данное собственное значение оператора равна квадрату абсолютного значения скалярного произведения текущего вектора состояния с соответствующим собственным вектором оператора.
Довольно абстрактно, не так ли?
Как я отмечал, многие постулаты взаимосвязаны. Например то, что скалярное произведение надо возводить именно в квадрат, а не в куб скажем, можно вывести из других постулатов.
Итак, применим эту математическую махину к знаменитому «парадоксу» кота Шредингера.
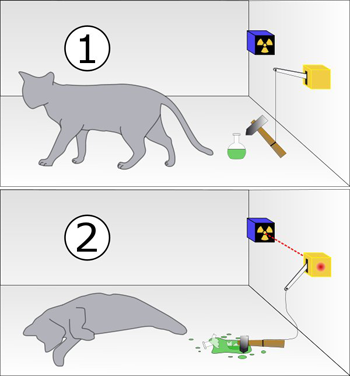
Нам надо измерить состояние кота (жив/мертв). Согласно постулату такой измеряемой величине должен соответствовать эрмитов оператор. И действительно, можно такой найти. Операторы, отвечающие на вопросы да/нет (жив ли кот?), называются операторами проекции. У них только два собственных значения – ноль и единица. Единица в нашем случае соответствует живому коту, ноль – мертвому.
Согласно постулату, при измерении мы можем получить только одно из этих двух собственных значений. Поэтому мы никогда не получим жив+мертв. Нет такого собственного значения, соответствующего вектору у нашего оператора проекции. Всё, «парадокс» исчерпан.
Но квантовая механика также позволяет посчитать вероятность того, что при наблюдении у нас окажется живой кот, и вероятность того, что мертвый. Скажем сейчас состояние кота описывается вектором . Вероятность, что при наблюдении кот будет жив, согласно правилу Борна равна:
и тому, что мертв:
Всё, нудные квантовомеханические вычисления закончены. Существуют теоремы, показывающие, что извлечь больше информации, нежели эти вероятности невозможно в принципе.
Многомировая интерпретация
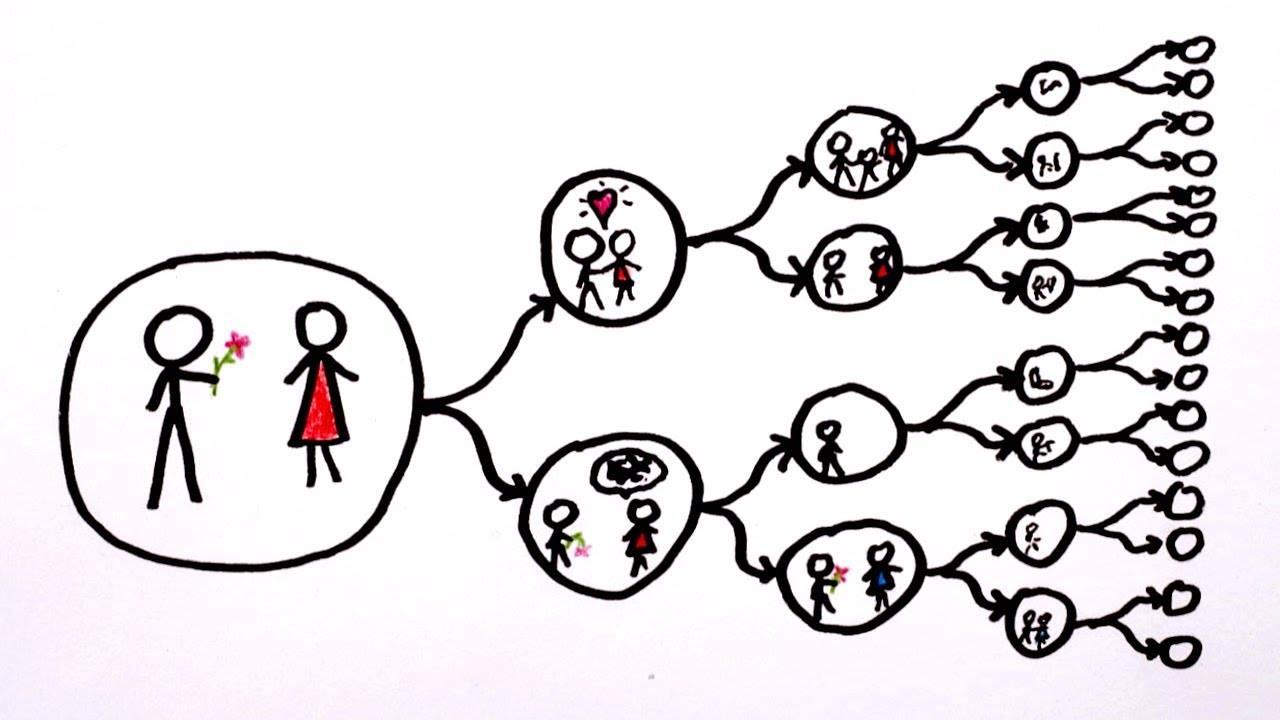
—
Адепты многомировой интерпретации просто отбрасывают два последних постулата. Они нам не нужны, лишние.
Но понятно, что если бы без них можно было обойтись, отцы-основатели их бы и не вводили. Чем же их заменяют сторонники многомировой? Как ни странно, многими мирами.
Все альтернативы реализуются в том или ином мире. Если система описывается вектором , то вселенная делится на два мира: в одном кот жив, а в другом мертв.

—
Гениально, не правда ли? И привлекательно чисто психологически. Приятно думать, что есть миры где вы миллиардер.
Но многомировая заходит в тупик если просто взять другие коэффициенты (амплитуды вероятности) перед векторами и . Возьмем, например:
Стандартная копенгагенская интерпретация говорит, что при наблюдении с 99%-ной вероятностью мы увидим мертвого кота. И поверьте мне, так оно и будет. Но что поменялось в многомировой? Ничего. Как было два мира, так и осталось. Вероятность должна быть 0.5.
Особо продвинутые адепты говорят, что «толщина ветки» поменялась. Но объясните мне, пожалуйста, от чего зависит эта толщина и что заставляет ее меняться? Чем слово «толщина ветки» отличается от слова «вероятность»? Все-таки вам необходимо правило Борна, просто вероятность заменяется толщиной? Ну ОК.
Вообще-то в оригинальной версии эксперимента, судьба кота связывается с тем распался атом или нет. Вероятность, что атом распался увеличивается с течением времени, а то что не распался уменьшается. В рамках стандартной копенгагенской интерпретации даже можно найти точную зависимость вероятности от времени.
У многомировых адептов видимо получается, что «толщина ветки» меняется со временем. В общем 1%-но реальный мир и 99%-но реальный мир как-то не очень красиво смотрятся.
Другая группа утверждает, что образуется сто миров.
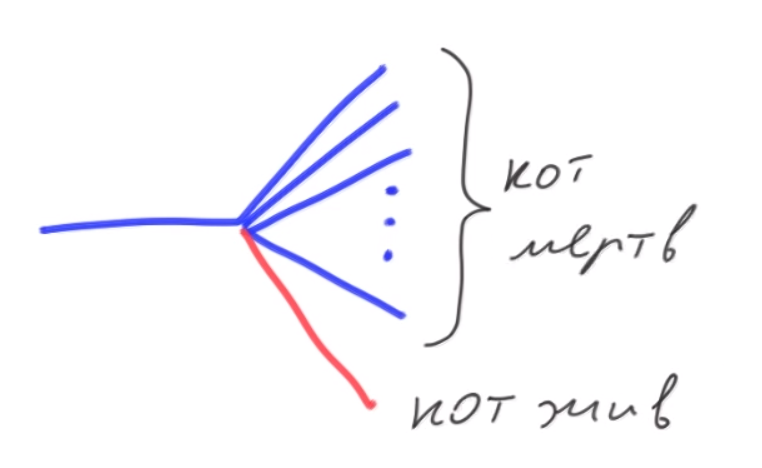
В одном кот жив, а в 99-ти мертв. Но откуда взялось сто, если слагаемых в суперпозиции всего два: жив+мертв? Утверждается ведь, что многомировая интерпретация не изменяет математику КМ. И опять же, вероятности меняются со временем. С течением времени появляется все больше и больше миров с мертвым котом? Даже если я оказался в мире с живым котом?
Кстати о времени. В представлении Гейзенберга вектор состояния вообще статичен, а со временем меняются операторы. Но многомировая интерпретация работает только в представлении Шредингера, когда эволюция во времени возложена на вектор состояния (волновую функцию). Получается все-таки она не со всей математикой стандартной КМ совместима, как заявляется.
Когда именно происходят эти разветвления? Согласятся ли о времени разветвления наблюдатели из разных систем отсчета? Кто-то вообще пытался скомбинировать многомировую с теорией относительности?
Еще один аргумент связан с таким нюансом квантовой механики, что наблюдатель может выбирать базис в котором будет измерена наблюдаемая величина. С котом Шредингера не совсем очевидно какой вообще другой базис можно использовать. Но если рассмотреть что-то «более квантовое», спин электрона например, то несмотря на то, что при измерении тоже получим только одно из двух значений (спин вверх или спин вниз), вид эрмитового оператора для спина будет разным для разного базиса. А их бесконечно много. Он связан с выбором оси относительно которой будет измеряться спин.

Но направлений в пространстве бесконечно много. Распределение вероятностей каким окажется спин при измерении зависит от выбранного направления (базиса).
Приделаем прибор по измерению спина к автомату, убивающему кота. Тогда окажется, что его судьба связана с результатом измерения спина и выбором наблюдателем определенного базиса. Получается экспериментатор определяет своим выбором на сколько миров поделится вселенная?
Сколько вообще образуется миров? Два для каждого из результатов измерения спина (вверх/вниз) и бесконечность для каждого из базисов? Два умножить на бесконечность?
А если измерять какую-то величину, оператор которой имеет непрерывный спектр. Например, в какую именно из бесконечного числа точек на экране попадет фотон, пройдя двухщелевую пластинку.
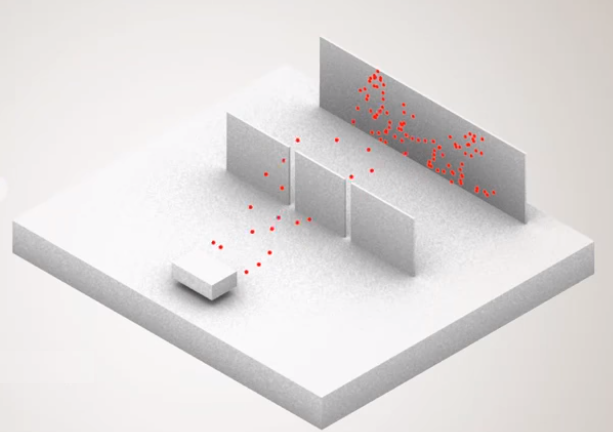
А если наблюдатель опять захочет сменить базис. Будет измерять не координату, а импульс. Сколько появится миров? Бесконечность умножить на два?
А если измерять величину с непрерывным спектром и выбрать базис можно из бесконечности возможностей. Сколько миров образуется? Бесконечность умножить на бесконечность?
ОК, я знаю, что Георг Кантор придумал кардинальные и ординальные числа для таких случаев. Идея для научных фриков: попробуйте описать многомировую интерпретацию с их использованием. Не зря же эти разные бесконечности в Платоновском мире идей существуют. Хоть для чего-нибудь сгодятся.
Можно привести и множество других аргументов. Почему и как эти миры могут опять объединяться, а они должны иметь возможность объединяться, ведь до измерения квантовая эволюция обратима. А поскольку в многомировой интерпретации убраны постулаты о измерении, то эволюция получается обратима всегда. Как объясняются эксперименты по квантовой запутанности? И так далее, и так далее…
В общем с этими крэйзи идеями Хью Эверетт пошел к самому Нильсу Бору, который над ним посмеялся.

Ха-ха
Что такое коллапс
Сторонники многомировой надеется, что правило Борна когда-нибудь будет получено из «физики деления миров». Вероятности не фундаментальны, говорят они. Я вас разочарую, но этого никогда не произойдет. Невозможно построить вероятностную теорию не вводя вероятности изначально.
Особо яро адепты критикуют постулат об измерении. Что же он означает?
При измерении вектор состояния (волновая функция) коллапсирует в один из собственных векторов оператора измеряемой величины. В случае кота Шредингера это векторы и . Постулат просто говорит: каким бы не был вектор состояния до измерения, если вы увидели живого кота, то теперь систему следует описывать вектором . Если же вы увидели мертвого кота, то описывать его теперь надо вектором .
То есть коллапс отражает обновление знаний наблюдателя при получении им новой информации. Это субъективный процесс. Никакой физический процесс не связан с коллапсом. И да, разные наблюдатели могут описывать одну и ту же систему разными векторами состояния. И коллапс для них может происходить в разное время. Это видно на примере мысленного эксперимента с другом Вигнера.
Можно провести аналогию с подбрасыванием монетки.

Изначально вы описываете систему вероятностями: 50%, что выпадет орел и 50%, что решка. Но после подбрасывания выпадает либо орел, либо решка. Вы обновляете свою информацию и описываете текущее состояние системы как 100% орел и 0% решка. Произошел «коллапс» распределения вероятностей в одну из реализовавшихся альтернатив.
Квантовая механика в ее стандартной Копенгагенской интерпретации субъективна. Из нее нельзя выкинуть ни наблюдателя ни наблюдение (измерение).
Фейнман о многомировой интерпретации

Ричарда Фейнмана принято приводить в качестве примера гуру по квантовой физике. Он уделил многомировой интерпретации целых 30 секунд из своей жизни. Этот момент сохранился в виде стенограммы конференции. Фейнман выразил мнение, что многомировая интерпретация – полная чушь и больше к ней никогда не возвращался.
Источник


