[Перевод] Спросите Итана: нарушает ли кульминация фильма «Гравитация» простейшие законы физики?

Фильмы играют важнейшую роль в стимуляции нашего воображения на тему будущего человечества, и очевиднее всего это проявляется в области космических путешествий. За последние несколько лет такие фильмы, как «Интерстеллар», «Марсианин» и «Гравитация» помогли нам представить, что станет возможным в будущем, но при этом оставили вопросы о том, насколько эти фильмы могут быть точны. Я получил такой вопрос от Троя Стюарта:

Мы с женой смотрели вечером «Гравитацию» и увидели то, что изображено на картинке ниже. Вопрос такой почему, когда Джордж отпускает натянутый фал, когда они висят в пространстве, он улетает? Ведь в этот момент вес одинаков и не играет роли. Жена считает, что они плывут в пространстве с разной скоростью из-за разницы масс. Я считаю, что масса играет роль только при попытке сменить направление. Так почему же Джордж улетает, отцепив себя?

И вот эта картинка.

В этой сцене два космонавта пролетают мимо Международной космической станции в отчаянной попытке добраться до неё. Там находится один из модулей «Союз» со сработавшим парашютом. Райан Стоун (Сандра Баллок) и Мэтт Ковальски (Джордж Клуни) пытаются зацепиться за него. У обоих ничего не получается, но Стоун цепляется за парашютную стропу ногой и держит Ковальски. Они видят, что шнур не выдержит их двоих, поэтому Ковальски отцепляется и медленно уплывает в космос, вдаль от Стоун и космической станции.

Но с этим сценарием есть одна проблема, описанная Троем. Судя по всему, она противоречит первому закону Ньютона.

Первый закон Ньютона можно назвать самым старым законом физики из известных человечеству: находящиеся в покое объекты сохраняют покой, а двигающиеся сохраняют направление и скорость движения, если на них не действуют внешние силы. После того, как Стоун и Ковальски поймали парашютную стропу, она натянулась и больше не растягивается, они должны двигаться с одинаковой скоростью и в одном направлении. С первого взгляда нет никаких причин даже для того, чтобы они натянули стропу – они двигались с постоянной скоростью, без ускорения, а значит и силы никакой нет. Но всё-таки Ковальски после отцепления улетает.

Суть в том, что здесь работают внешние силы. Есть сила притяжения Земли, к примеру. Есть небольшое, но не пренебрежимо малое, воздействие со стороны разреженной атмосферы (поэтому спутники на низких орбитах периодически нужно приподнимать, иначе они сойдут с орбиты и сгорят в атмосфере). Международная космическая станция гораздо массивнее Стоуна или Ковальски, поэтому она больше подвержена гравитации. Но это не должно иметь значения, поскольку третий закон Ньютона, утверждающий, что F = ma, говорит, что ускорения у МКС, Стоун и Ковальски должны быть одинаковыми, даже при разной массе.

Воздействие атмосферы – тоже интересный вопрос. Она зависит от плотности объекта, площади его поверхности и размера. По этой причине, если бы Галилей действительно ставил свой эксперимент по сбрасыванию двух шаров разной массы и одинакового размера с наклонённой башни в Пизе, он бы обнаружил, что более тяжёлый мяч долетел до земли быстрее: по сравнению с шаром весом в 5 кг, шар весом в 500 г испытывал бы всего лишь 10% притяжения но 22% сопротивления воздуха! Более лёгкий и менее плотный объект, чем МКС – например, человек – будет испытывать большее тянущее усилие со стороны атмосферы, и поэтому будет активнее замедляться, будучи на орбите.

Но этого недостаточно для происходящего в фильме. Плотность воздуха на высоте МКС настолько мала, что потребовались бы месяцы на то, чтобы Ковальски снесло в сторону. Его можно было отправить в сторону космического корабля простым рывком за трос, и это обесценило бы весь эпизод.

Но кое-что, если рассматривать постер фильма, как истину, мы не учли. Что, если мы не будем рассматривать трос, как линейную систему, а отметим, что в расположении объектов присутствуют углы?

Ковальски, очевидно, расположен под углом к Стоун, которая расположена под углом к МКС. Что могло привести к такому положению в космосе? Вращение космического аппарата! К этому может привести даже небольшое вращение, вызванное недавним запуском или столкновением (как оно и происходит в фильме), произошедшим в любом месте, кроме центра масс МКС. Если вы когда-нибудь вращали мяч на верёвке, а потом перерезали её, вы знаете, что мяч улетает прочь по прямой линии.

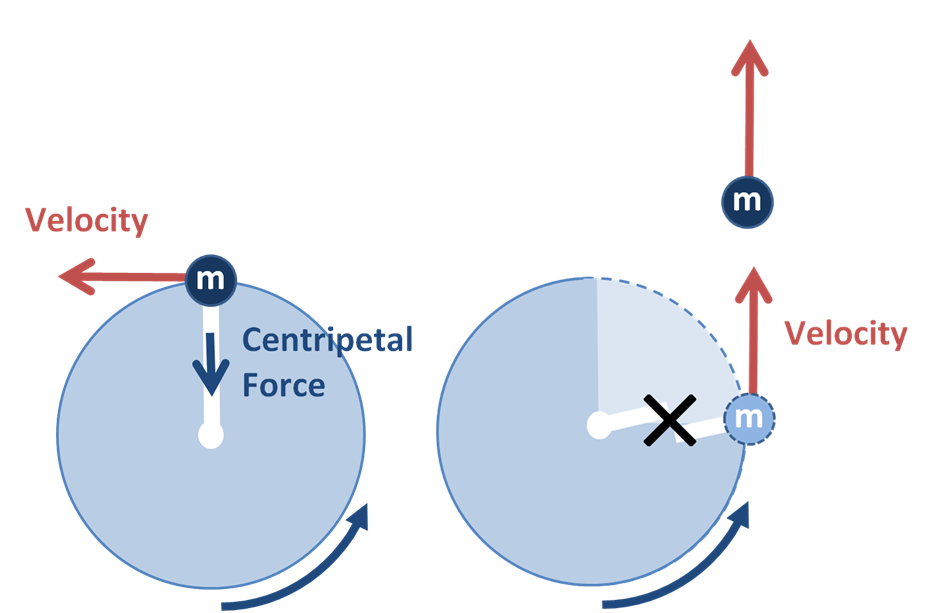
В космосе такое вращение может быть очень медленным. Таким медленным, что оно может практически не восприниматься при просмотре эпизода. Но его может хватить на то, чтобы:
• Держать трос натянутым.
• Обеспечить риск того, что масса на конце троса может его порвать.
• Если находящийся на конце вес отцепится (Ковальски отпустит трос), он будет двигаться прочь под действием инерции.

Так что, Трой, ты прав, какой-то из видом ускорения необходим для того, чтобы натягивать трос, рисковать порвать его, а также сдвинуть Ковальского, когда он отпустит трос, прочь от станции. Это ускорение может быть вызвано внешней силой, вызывающей изменение вашей скорости, или вращательным движением, вызывающим смену направления. На основании увиденного в фильме я выбираю изменение направления: небольшое, но достаточное для того, чтобы вызвать показанный в фильме эффект.

Возможно, я не смотрю фильмы так, как это делает большинство учёных. Я не выискиваю недостатки или дыры сюжета, не говорю: «это невозможно!». Я пытаюсь примирить происходящее с возможностями, предоставляемыми законами физики, и здесь я нашёл такой вариант. Вращение также играло большую роль и в фильме «Марсианин»; там был один момент, когда мне захотелось закричать на Мэтта Деймона, проткнувшего дыру в рукаве своего скафандра – я не мог понять, почему он не держал её ближе к своему центру масс, чтобы лучше контролировать полёт!

В итоге, такой опытный космонавт, как Ковальски, мог бы попробовать сделать один мощный рывок, чтобы приблизиться к станции, если только её вращение не было большим, чем это было видно в фильме – тогда такой манёвр был бы невозможным. Но ускорение любого рода – единственная причина, по которой космонавт, отцепившись, начал бы улетать прочь. Так что объяснение такому эффекту должно быть. Ну или киношники просто решили, что сюжет, история и развязка важнее науки, и они просто ждали появления не особенно привередливого астрофизика, который дал бы всему происходящему подходящее объяснение!