[Перевод] Инженерный анализ схемы ускоренного переноса процессора Intel 8008

В 1972 году Intel представили свой первый 8-битный микропроцессор – 8008. Несмотря на свою примитивность в сравнении с современными стандартами, Intel 8008 важен исторически, потому что именно он положил начало микропроцессорной революции и является предком современного семейства процессоров x86. Я поизучал кремниевый кристалл этого процессора под микроскопом и произвел инженерный анализ его схемы.
На нижеприведенном фото кристалла показаны главные функциональные блоки ¹, включая регистры, декодер команд и хранилище стека. 8-битное арифметико-логическое устройство (АЛУ) находится слева. Над ним расположен генератор ускоренного переноса, повышающий производительность путем упреждающего вычисления переносов суммирования до выполнения самого суммирования. Немного удивительно видеть реализацию ускоренного переноса в столь ранней модели процессора. Но раз она в нем есть, то есть повод рассказать вам о способе ее технической реализации.

Кристалл Intel 8008 и его ключевые функциональные блоки.

Большая часть из того, что вы видите на фото кристалла – это верхняя зеленовато-белая разводка металлического слоя. Под металлом находится разводка из поликремния, обеспечивающая большее число соединений, а также реализующая транзисторы, которые можно отличить по ярко-желтому цвету. Их в этой микросхеме насчитывается около 3 500. Расположенная еще ниже кремниевая подложка представлена пурпурно-серым цветом и большей частью скрыта. Вдоль краев кристалла размещены 18 прямоугольных площадок, которые крошечными проводками подключены к внешним контактам корпуса самой интегральной схемы (показана ниже).

Интегральная схема Intel 8008 в 18-контактном DIP (корпус с двухрядным расположением выводов). Этот корпус сильно пошарпан, но я не видел смысла переплачивать за идеальное состояние чипа, который предполагалось тут же вскрыть.

Intel 8008 продавался в виде миниатюрной 18-контактной интегральной схемы в DIP. 18 – это неудобно маленькое число контактов для микропроцессора, но Intel придерживались в то время именно небольших корпусов². Для сравнения, другие ранние микропроцессоры обычно задействовали 40 контактов, что существенно облегчало подключение к процессору шины данных, шины адреса, шины управления и питания.

Сложение

Сердце процессора – это арифметико-логическое устройство, функциональный блок, выполняющий арифметические (например, сложение или вычитание) и логические (например, AND, OR и XOR) операции. Эффективная реализация сложения вызывала наибольшие сложности из-за необходимости переносов ³.

Для наглядного представления процесса рассмотрим сложение столбиком двух десятичных чисел 8888 и 1114. Начиная с крайнего правого разряда, вы складываете каждую пару цифр (8 и 4), записываете их сумму (2) и переносите остаток (1) влево. В следующем разряде вы складываете очередную пару цифр (8 и 1) и перенос (1), записывая сумму (0) и снова перенося (1) в следующий разряд. Продолжая таким образом переходить все левее, вы в итоге получите результат 10002. Имейте в виду, что вычисление разрядов происходит строго поочередно и пропуски не допускаются.

Двоичные числа можно складывать аналогичным образом с помощью схемы под названием каскадный сумматор, применяющейся во многих микропроцессорах. В ней каждый бит вычисляется полным сумматором, который получает на входе два бита и перенос, производя суммированный бит и выходной перенос. Например, двоичное сложение 1 + 1 без входного переноса производит 10, где суммированный бит равен 0, а выходной перенос 1. Каждый выходной перенос прибавляется к биту, расположенному слева также, как и в десятичном сложении столбиком.

Проблема каскадного сумматора в том, что при сложении, скажем, 11111111 + 1, вы вынуждены ждать пока перенос распространится через все биты справа налево. Поэтому сложение вместо того, чтобы быть параллельной операцией становится последовательной. Несмотря на то, что Intel 8008 выполняет сложение только 8-битных чисел, такая задержка замедлила бы его работу слишком сильно. Решением оказалось применение схемы ускоренного переноса, которая оперативно вычисляет переносы для всех 8 позиций битов. После этого полученная сумма может вычисляться параллельно, не требуя ожидания сквозного прохождения переноса через все биты. Как сказал тогда сам проектировщик Intel 8008 Хэл Фини:

«Мы разработали логику упреждающего переноса, потому что нуждались в повышении скорости со стороны процессора. Ее схема показалась нам весьма удобной для интегрирования, не требующей больших накладных расходов и много места для своего размещения. Обратите внимание, что она вся занимает очень небольшую часть микросхемы».

Реализация ускоренного переноса

Идея ускоренного переноса в том, что, если есть возможность вычислять все значения переносов наперед, значит можно быстро суммировать все позиции битов параллельно. Но как тогда вычислить перенос, не выполняя сложение? В Intel 8008 решением было собрать отдельную схему для каждой позиции бита, чтобы вычислять переносы на основе входных значений.

На диаграмме ниже в увеличенном масштабе представлены схема ускоренного переноса и арифметико-логическое устройство. Два 8-битных аргумента и входной перенос поступают сверху. Эти значения переходят по вертикали через схему ускоренного переноса, по пути генерируя значения переносов для каждого бита. Каждый блок АЛУ получает два входных бита и бит переноса, производя один выходной бит. Схема ускоренного переноса имеет треугольную структуру, потому что последующие биты переноса требуют все больше цепей, что будет объяснено позже. Необычная форма 8-битного АЛУ объясняется стремлением максимально задействовать площадь треугольника. Практически во всех микропроцессорах АЛУ располагается в прямоугольном блоке. 8-битное АЛУ тоже должно иметь 8 похожих частей, но в Intel 8008 эти части распределены неравномерно, а некоторые даже повернуты боком. Я уже писал статью про арифметико-логическое устройство этого процессора, так что можете ознакомиться в ней с подробностями.

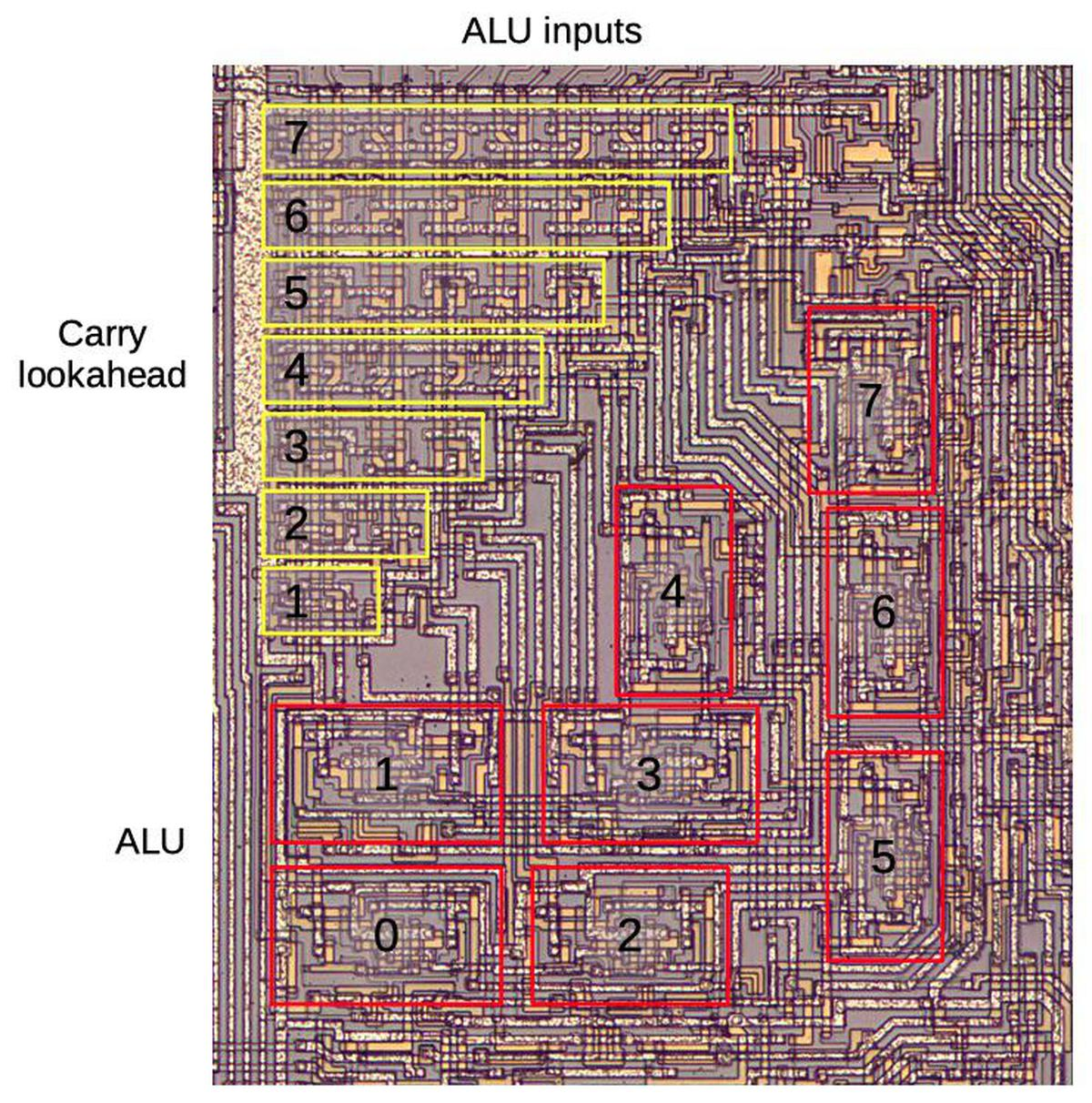
Увеличенный сегмент кристалла Intel 8008 со схемой ускоренного переноса и АЛУ.

Чтобы представить принцип работы ускоренного переноса, рассмотрим три случая сложения. Первый – это сложение 0+0. Этот вариант не может создать перенос, даже если таковой поступит на входе. Сумма в данном случае будет 0 при отсутствии входного переноса или 1 при его наличии. Второй вариант – это 0+1 или 1+0. Здесь перенос возникнет только, если он изначально будет подан на входе. С входным переносом результат будет 10, без него 1. Это ситуация «распространения», поскольку входной перенос распространяется в выходной. Последний случай сложения – это 1+1. Здесь перенос возникнет независимо от наличия входного переноса, а сам случай рассматривается как случай «генерации», поскольку происходит именно генерация переноса.

Показанная ниже схема вычисляет выходной перенос при сложении двух битов (X и Y) и входного переноса. Данная схема состоит из затвора OR слева, двух затворов AND в середине и затвора OR справа. (Несмотря на то, что выглядит эта схема сложной, она очень эффективно реализуется в устройствах). Чтобы увидеть, как она работает, рассмотрите три случая. Если X и Y оба равны 0, выходной перенос будет 0. В противном случае первый затвор OR выведет 1. Если входной перенос будет 1, то верхний затвор AND выведет 1, и перенос будет 1 (случай распространения). И наконец, если как X, так и Y будут 1, то нижний затвор AND выведет 1, и выходной перенос тоже будет 1 (случай генерации).

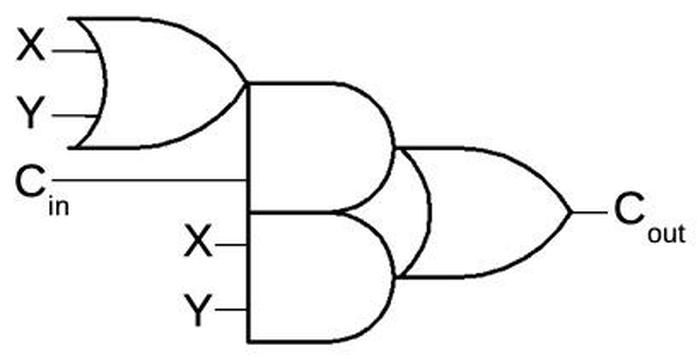
Эта схема вычисляет выходной перенос при получении входного переноса и двух входных бит X и Y.

Чтобы вычислить перенос для более высокого разряда, можно объединить несколько экземпляров этой схемы. Например, схема ниже вычисляет перенос в позиции 2-го бита (C₂). Блок затвора слева вычисляет C₁, перенос в позиции 1-го бита из входного переноса (С₀) и битов нижнего разряда X₀ и Y₀, как и объяснялось выше. Затворы справа применяют тот же процесс к следующим битам, генерируя перенос в позиции 2. Для других позиций битов используется тот же принцип, но с дополнительными блоками затворов. Например, перенос в позиции 7 вычисляется цепочкой из семи блоков затворов. Поскольку эта схема для каждого последующего бита становится на одну единицу длиннее, общая структура переноса реализуется в треугольном виде, как мы видели на кристалле.

Для вычисления переноса в позиции 2 необходимо два каскада его прогнозирования.

Нижеприведенный чертеж показывает, как на кристалле реализована схема переноса для 2-го бита. Схема для других битов аналогична, просто содержит больше повторяющихся блоков. На фотографии металлическая проводка верхней части кристалла имеет серебристый цвет. Под ней располагается желтая поликремниевая проводка. Самая же нижняя кремниевая часть окрашена в сероватый оттенок. Под фотографией приведена схема подключения транзисторов. Расположение элементов на этой схеме близко к их физическому расположению.

Реализация схемы ускоренного переноса для 2-го бита.

Я вкратце поясню, как эта схема работает. В реализации Intel 8008 использован тип транзисторов под названием PMOS. Принцип действия такого транзистора можно представить как открывание при входном 0 и закрывание при входной 1⁴. Вместо стандартного затвора логики эта схема использует технику динамической логики, основанную на емкостном сопротивлении. Первым шагом сигнал предварительной зарядки подается на схему -9В, предварительно заряжая ее. Вторым шагом применяются входные сигналы (сверху), активируя разные транзисторы. Если образуется проход через транзисторы от питания +5В к выходу, то напряжение на выходе возрастает. В противном случае его значение остается на уровне предварительного заряда. Емкостное сопротивление проводов сохраняет значение -9В. Я не будут комментировать всю цепь, но верхние пары транзисторов X/Y реализуют затвор OR, так как, если любой из них активен, то перенос может пройти. Нижние транзисторы X/Y реализуют затвор AND, т.е. если они оба окажутся активны, то пропустят сигнал +5В, сгенерировав 1.

Вам может стать интересно, почему эта схема ускоренного переноса быстрее простого каскадного сумматора, ведь этому сигналу переноса для генерации итогового бита переноса необходимо пройти вплоть до 7 затворов. Хитрость в том, что вся эта схема благодаря своей динамической структуре электрически представляет собой один огромный затвор. Все транзисторы активируются параллельно, после чего сигнал 5В может все их пройти очень быстро⁵. Хоть здесь и присутствует небольшая задержка, вызванная перемещением сигнала по цепи, эта схема намного быстрее, чем стандартный каскадный сумматор, активирующий транзисторы последовательно.

Краткая история схем переноса

Эффективная обработка переносов вызывала сложности еще на ранних этапах механических вычислений. Математик Блез Паскаль в 1645 году создал суммирующую машину, которая задействовала работавший на гравитации механизм сквозного переноса. Этот механизм стремительно распространял перенос от одной цифры к другой (видео). Почти два века спустя, Чарльз Бэббидж спроектировал известную разностную машину (1819 – 1842). В ней использовался медленный сквозной перенос: после цикла сложения спиральные рычаги на вращающемся валу активировали перенос каждой цифры последовательно. После этого Бэббидж провел многие годы разрабатывая улучшенную механику переноса уже для другой своей многообещающей Аналитической машины (1937), спроектировав «опережающий механизм», который должен был осуществлять все переносы параллельно. Этот сложный механизм предусматривал наличие в зубчатом колесе каждой цифры скользящего стержня, который при переключении колеса на цифру 9 задвигался в соответствующее положение. Когда цифра активировала перенос, сменяясь с 9 на 0, механизм поднимал стек этих стержней, параллельно увеличивая соответствующие цифры (видео).

Подробная схема «опережающего механизма», вычисляющего переносы в Аналитической машине. Принцип ее работы мне до конца не понятен. Чертеж взят из The Babbage Papers at the Science Museum, London, CC BY-NC-SA 4.0.

В первых цифровых компьютерах использовался сквозной перенос. Инженер, работавший над релейной вычислительной машиной Bell Labs (1939) утверждал, что «схема переноса оказалась сложна» из-за использования двоично-десятичного кода (BCD). Революционный ENIAC (1946) задействовал десятичные счетчики со сквозным переносом. Первые компьютеры с двоичной электроникой, такие как EDSAC (1949) и SEAC (1950) были последовательными, обрабатывая по одному биту за раз, в связи с чем и переносы они вычисляли по одному биту за раз. Первые компьютеры с параллельным сложением, такие как SWAC 1950 года (самый быстрый компьютер того времени) и коммерческий IBM 701 (1952) использовали сквозной перенос.

Так как в 50-х годах компьютеры стали уже шустрее, сквозной перенос начал ограничивать их производительность, в связи с чем были разработаны альтернативные решения. В 1956 году Национальное бюро стандартов запатентовало 53-битный сумматор, работавший на вакуумных трубках. Такой дизайн ввел в индустрию значимый принцип ускоренного переноса наряду с идеей использования иерархии переноса (в данном случае двух уровней). Схема ниже иллюстрирует сложность этого сумматора.

Структура 53-битного сумматора из A 1-microsecond adder using one-megacycle circuitry, 1956 год.

Разработка суперкомпьютеров привела к появлению новых технологий. В 1962 году в Манчестерском университете при участии компаний Ferranti и Plessey был собран транзисторный Atlas. В нем использовалась внушительная техника манчестерских цепей переноса, описанная в 1959 году. Atlas соперничал с IBM Scretch (1961) за титул самого быстрого в мире компьютера. В Scretch были реализованы новейшие высокоскоростные техники, включая сумматор с переключением переноса и запатентованный сумматор с сохранением переноса для умножения.

Как и в случае с мейнфреймами, микропроцессоры начали с простых сумматоров, но с ростом потребности в производительности стали нуждаться в более совершенных техниках переноса. Большинство ранних версий микропроцессоров задействовали сквозной перенос, как, например, в 6502, Z-80 и ARM-1. Пропуск переноса частенько использовался для счетчиков команд (как в 6502 и Z-80). Скорости сквозного переноса было достаточно для 8-битных слов, но уже существенно не хватало для 16-битных счетчиков команд. В АЛУ процессора Intel 8086 (1978) использовалась манчестерская цепь переноса совместно с пропуском переноса. Большое количество транзисторов в микросхемах СБИС позволяло применять более сложные сумматоры, полученные в ходе исследований сумматоров с параллельным префиксом. DEC Alpha 21064 (1992) совмещал в себе несколько техник: манчестерскую цепь переноса, ускоренный перенос, условное суммирование и сумматор с переключением переноса (подробнее). В Hewlett-Packard PA_8000 (1995) содержалось более 20 сумматоров, предназначавшихся для разных целей, включая сумматор Линг, который был разработан IBM в 1966 году (подробнее). В Pentium II (1997) был применен 72-битный сумматор Когге-Стоуна, а в Pentium 4 сумматор Хан-Карлсона⁶

Приведенные исторические факты показывают, что распространение переноса являлось важной проблемой производительности еще в 50-е годы и вызывает сложности по сей день, в связи с чем исследования и поиск более совершенных механизмов продолжаются. За это время уже было разработано множество различных решений, сначала для мейнфреймов, а затем и для микропроцессоров. Сложность подобных решений возрастает параллельно с техническим прогрессом. У каждого подхода есть свои недостатки, проявляющиеся в площади кристалла, стоимости и скорости. Поэтому в разных процессорах задействуются разные их реализации.

Фото кристалла процессора Intel 8008.

Если вы хотите побольше узнать об Intel 8008, то у меня есть ряд других статей, где я описываю его архитектуру, АЛУ, стек микросхемы, начальную загрузку и необычную историю этого микропроцессора.
О свежих материалах я пишу в Twitter, так что можете подписаться на мой аккаунт @kenshirriff. У меня также есть RSS лента.

Заметки и ссылки

1. Функциональные блоки Intel 8008 подробно описаны в его прикрепленном ниже паспорте. Расположение элементов представленной схемы очень близко к их физическому расположению на кристалле. Желтым выделен блок ускоренного переноса.

Функциональные блоки 8008 процессора из его паспорта.

2. Как рассказывал Федерико Фаггин, команде инженеров, разрабатывавших Intel 8008, посчастливилось использовать для своего детища 18-контактный корпус. «В Intel это был некий канон» применять 16-контактные корпуса несмотря на то, что другие производители, как правило, использовали 40- или 48-контактные. Когда Intel были вынуждены перейти на 18-контактные корпуса для микросхемы ОЗУ 1103, это решение прогремело, как «гром среди ясного неба. Такое количество одновременно вытянувшихся лиц в этой компании мне еще видеть не доводилось.» Переход на 18 контактов оказался на руку команде Intel 8008, которая при разработке предыдущей версии Intel 4004 довольствовалась 16-контактным корпусом. Тем не менее даже 18 контактов категорически не хватало с учетом того, что микросхема использовала 14-битные адреса. В результате сигналы адресов и данных мультиплексировались на 8 контактах для передачи данных. Это как замедляло сам процессор, так и усложняло использование микросхемы. Вскоре Intel отказались от использования маленьких корпусов и в 1974 году перешли на стандартные 40-контактные, начав с их применения для процессора 8080.

3. Здесь я игнорирую вычитание, потому что оно было реализовано операцией сложения с добавлением значения дополнительного кода. Умножение и деление в ранних микропроцессорах не использовалось. При этом очень интересно, что даже в ранних мейнфреймах эти операции все-таки аппаратно реализовывались.

4. Большинство «классических» микропроцессоров создавались на транзисторах NMOS. Если вы знакомы с затворами NMOS, то в PMOS все наоборот. Несмотря на то, что в производительности PMOS уступают NMOS, по началу они были проще в производстве, поэтому и использовались в процессорах Intel 4004 и 8008. Эти транзисторы требовали довольно больших отрицательных напряжений, почему на схеме и показаны -9В и +5В.

5. Я активно работаю над определением тайминга схемы ускоренного переноса. Точный анализ тайминга потребует учета емкостного сопротивления на каждом каскаде, что может добавить член O(n2).

Обратите также внимание, что эта схема ускоренного переноса несколько необычна. В ее стандартном варианте (например, в микросхеме АЛУ 74181) затворы расширяются, что существенно увеличивает схему, но при этом делает ее более плоской, минимизируя тем самым задержки распространения. С другой стороны, схема Intel 8008 имеет много общего с манчестерской цепью переноса, которая использует аналогичную технику передачи входящего переноса через цепочку проходных транзисторов или потенциальной генерации переноса на каждом каскаде. Тем не менее манчестерская цепь переноса задействует одну цепочку N-каскада вместо треугольной структуры раздельных цепей для каждого бита в Intel 8008. Она может выбирать перенос каждого бита с каждого каскада цепи, поэтому и требуется всего одна цепь. При этом схеме переноса Intel 8008 недостает транзисторов, блокирующих распространение переноса назад, в связи с чем его промежуточные значения могут оказаться не действительными.

Как бы то ни было, для нужд Intel быстродействия схемы ускоренного переноса, реализованной в Intel 8008, было достаточно.

6. Дополнительную информацию по различным сумматорам можете найти в этой презентации, этой и в справочном материале “Advanced Arithmetic Techniques”.