Немного о явлении испарения Хокинга

Несмотря на большой интерес к этой теме очень многие источники и практически все научно популярные неверно объясняют это явление. Причина в том, что первоначально некорректную эвристическую интерпретацию своего  открытия привел сам С. Хокинг, а именно: привлекая комбинацию квантовой физики и теории гравитации Эйнштейна, он обьяснял, что спонтанное рождение и аннигиляция пар частиц могут происходить вблизи горизонта событий. Обычно частица и ее античастица рождаются из квантового поля на очень короткое время, после чего тут же аннигилируют. Но иногда может произойти так, что одна частица падает за горизонт событий в черную дыру, а другая убегает.  Убежавшая частица, отдалившись от оппонентки на расстояние больше гейзенберговского, превращается в реальную и мы можем ее зафиксировать как излучение. Энергия реальных частиц равна произведению массы на квадрат скорости света, когда частица находится в покое, а с началом движения частицы возрастает; следовательно, энергия никогда не может быть отрицательной. Таким образом, если у реальной частицы, убежавшей от черной дыры, положительная энергия, а общая энергия исходной виртуальной пары была нулевой, значит, у частицы, упавшей в черную дыру, энергия отрицательная. И когда эта частица падает в черную дыру, общая масса черной дыры уменьшается.

По мнению самого Хокинга, этот процесс в конечном итоге должен приводить к испарению черной дыры. Однако даже невооруженным взглядом видны серьезные недостатки данного объяснения. Существует множество научных статей указывающих на ошибки этой интерпретации, например, можно порекомендовать блестящую статью [1] , однако наша цель привести более корректное объяснение испарению Хокинга.

Прежде всего напомним некоторые сведения о поведении времени-пространства в окрестностях черной дыры. Внешний наблюдатель, следящий за процессами вблизи горизонта событий черной дыры, видит, что частицы, падающие на черную дыру, никогда не достигнут горизонта событий за конечное время. Это связано с тем, что гравитационное притяжение черной дыры так велико, что частицы, падающие в нее, очень сильно замедляют свое движение, пока они приближаются к горизонту событий.

Согласно общей теории относительности, когда объект приближается к горизонту событий, время для него замедляется с точки зрения внешнего наблюдателя. Это означает, что для внешнего наблюдателя падение частицы к горизонту событий занимает бесконечно долгое время, так как время для этой частицы замедляется до бесконечности. Таким образом, с точки зрения внешнего наблюдателя, частицы, падающие в черную дыру, никогда не пересекут горизонт событий за конечное время.

Приведём соответствующие выкладки. (В дальнейшем все тексты на курсиве можно пропускать, так как они требуют достаточной математической подготовки).

Для простоты возьмем самый экстремальный случай радиального движения частицы к черной дыре и уравнение ее геодезической:

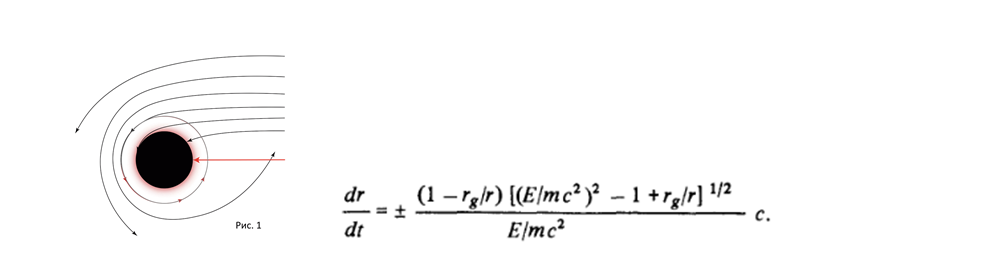
Время движения частицы от r = r₁  до горизонта событий  r = r _g определяется интегрированием этого уравнения, причем полученный интеграл расходится, что говорит о бесконечном времени падения частицы на черную дыру [1].

Таким образом, структура областей внутри черной дыры решающим образом зависит от судьбы черной дыры в бесконечном будущем внешнего наблюдателя, например, от конечного состояния испарения черной дыры, от возможных столкновений черной дыры с другими черными дырами и от судьбы самой Вселенной. Ясно, что теоретики чувствуют себя весьма неуютно и всеми силами уходят от такой постановки вопроса, перенося исследования на внутреннее время как падающей частицы, так и самой черной дыры. Эти изыски  представляются контрпродуктивным, так как  никоим образом не могут сказываться на процессах внешней Вселенной, поскольку время существования Вселенной- меньше времени достижения частицей горизонта событий. И кроме того   вновь рождаются  «нерешаемые» вопросы, как то.

а) интерпретация процесса трансформации пространства-времени на горизонте событий  и  за ним, поскольку  свойства пространства становятся  временно подобными, а свойства времени пространственно подобными.

б)  трансформация материи и энергии за горизонтом

в)  существование в этом «новом пространстве» обычной материи и энергии.

Кроме того, падений массовых и безмассовых частиц за горизонт событий  за конечное время нет, а испарение черной дыры происходит за конечное время [2]:

Далее всюду:  ℏ — приведенная постоянная Планка, c — скорость света в вакууме, G — гравитационная постоянная, M — масса черной дыры.

Мы  приведем     механизм испарения черных дыр, который не использует горизонт событий, тем самым решая указанные  проблемы.

Наша интерпретация использует подход  аналогичный  эффекту Швингера [3]  суть которого  состоит в том, что частицы самопроизвольно созданной виртуальной пары ускоряются в противоположных направлениях внешним электромагнитным фоновым полем. Если частицы разделяются достаточно далеко за время, отведенное им по принципу неопределенности Гейзенберга, то есть, если виртуальные частицы набирают достаточно энергии на расстоянии комптоновской длины волны, чтобы подчиняться релятивистской энергии  соотношения импульсов E2 = m2 + ⃗p2, они становятся реальными.

В пространстве-времени кривизна  будет играть ту же роль, что и напряженность электрического поля в эффекте Швингера.  По мере приближения к горизонту событий  искривление пространства  стремительно увеличивается, а приливные силы   становятся все более неравномерными. В силу этого часть виртуальных пар будет разделяться  этими силами и становиться реальными. Далее  какая-то их часть убежит от черной дыры, часть аннигилирует и часть будет вновь захвачена, в соответствии со стандартной долей убегания безмассовых частиц, рождающихся вблизи черной дыры (см. рис. 2 )

Рассмотрим формальное представление рождения виртуальных частиц в области черной дыры от  горизонта событий до бесконечности, а в дальнейшем приведем краткое математическое обоснование.

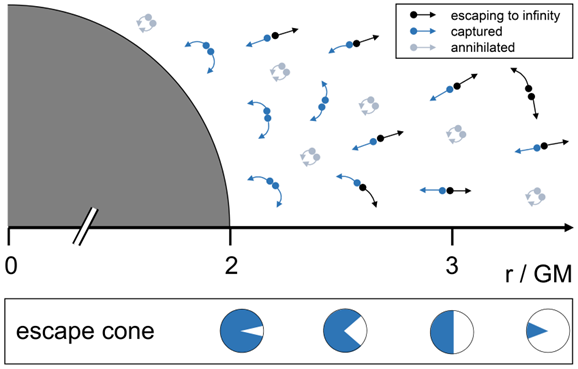
Как говорилось выше, в областях размером ниже гейзенберговских постоянно рождаются виртуальные частицы. В обычном плоском пространстве частицы не успевают разлететься и аннигилируют, но если пространство сильно искривлено, то это помогает частицам разлететься. Подсчитывая с помощью введенного подхода статистику, определяется, что частота событий образования частиц самая высокая на небольших расстояниях от горизонта событий, тогда как вероятность убегания самая высокая на больших расстояниях (шкала escape cone  на рисунке 1).

Кроме того, математический аппарат позволяет  посчитать радиальный профиль образования частиц, уходящих на бесконечность, за единицу времени внешнего наблюдателя :от резкого падения к горизонту событий до степенного уменьшения на больших расстояниях. Самая высокая плотность рождения убежавших частиц наблюдается при 2,32GM, тогда как наибольшее количество частиц на сферическую оболочку равно прибл. 2.47GM, что находится примерно на полпути между горизонтом событий и круговой фотонной орбитой в 3GM.

Далее оценивается  поток энергии созданных частиц на бесконечности и выводится энергия гравитационно созданной частицы.

Сравнивая число частиц и поток энергии со случаем Хокинга, устанавливается, что оба эффекта имеют одинаковый порядок. Представленный механизм рождения пар сам по себе не использует явным образом наличие горизонта событий  и не противоречит введенным ранее ограничениям.

Понятно, что если существует излучение без внешнего энергетического источника, то это означает, что пространство-время не стационарно. Следовательно,  черная дыра действительно испаряется.

Последнее утверждение требует особого внимания. Оно говорит что  в области пространства, содержащей черную дыру происходит уменьшение гравитационного поля и «распрямление» пространства. Это означает что происходит уменьшение массы вещества в этой области и следовательно в силу адиабатического принципа уменьшение массы самой черной дыры.

Кроме того, в силу ограничения о проникновении частиц за горизонт событий по времени внешней Вселенной, мы избегаем информационного парадокса следующим образом. Понятие информационного парадокса тесно связано с унитарностью квантовых операций и лишь нарушение унитарности ведет к потере информации. После гравитационного коллапса, с точки зрения внешней Вселенной в черной дыре не происходит никаких изменений, в том числе никаких преобразований (ни унитарных и никаких других прочих). В черную дыру не попадает никакой материи и энергии. Описанные выше механизмы рождения и убегания частиц, обеспечивающие испарение черных дыр — унитарны. Следовательно, всюду присутствуют только унитарные операторы и нет предпосылок для создания информационного парадокса.

Грубо говоря для квантовых физиков необходима унитарность, без нее все здание квантовой физики рухнет. Все остальные вопросы про информацию никого не трогают. К примеру все процессы в макромире сопровождаются ростом энтропии (согласно законам термодинамики), которая в конце концов поглотит всю информацию — и что? Физиков эта информация не заботит, поэтому и нет разговоров. На самом деле этот парадокс ничего не стоит, пропадает она ли, сгорает ли, восстанавливается — что это меняет? Ничего. А вот унитарность это -да. Это святое.

Рождение частиц.

Для построения математической модели будет использоваться идея однопетлевого эффективного действия. В квантовой теории поля эффективное действие может быть использовано для описания поведения поля на некоторых энергетических или временных масштабах, игнорируя подробности масштабов, которые слишком малы или слишком большие для интересующего нас явления.

 Обратимся к рисунку 1. Что бы реализовать   визуализированные идеи , нам надо ввести карту области вблизи черной дыры, смоделировать рождение и поведение частиц, и набрать статистику  убежавших частиц. Для этих целей мы будем использовать следующие понятия из квантовой теории поля : классическое действие W (или эффективное действие)  и однопетлевое эффективное действие W_E. Физический смысл W заключается в том, что оно представляет  карту области на рисунке 1, и  характеризует поведение частиц на этой карте, W_эфф отвечает за виртуальные частицы на этой карте.

 В квантовой теории поля эффективное действие может быть использовано для описания поведения поля на некоторых энергетических или временных масштабах, игнорируя подробности масштабов, которые слишком малы или слишком большие для интересующего нас явления. Действие W электромагнитного поля является скалярной функцией полей Aμ​ (векторного потенциала) и может быть записано как интеграл Лагранжиана по всему пространству-времени. Оно описывает, как электромагнитное поле взаимодействует с заряженными частицами и само с собой. Например, классическое действия W для взаимодействия заряженной частицы с фоновым электромагнитным полем. Предположим, что данная частица имеет заряд q, а фоновое электромагнитное поле характеризуется потенциалом Aμ​ и тензором электромагнитной поля Fμν​. Тогда классическое действие W может быть записано следующим образом:

W=−m∫ds+q∫Aμ​dxμ

где первый интеграл представляет действие для движения частицы в пространстве-времени, а второй интеграл представляет действие для ее взаимодействия с электромагнитным полем.

Теперь перейдем к однопетлевому эффективному действию W_E. Это включает в себя квантовые поправки к классическому действию, учитывающие взаимодействие частицы с виртуальными квантами электромагнитного поля. Формула для однопетлевого эффективного действия может быть записана как сумма классического действия и поправок в одной петле:

W_E ​=W+δW(1)

δS(1) представляет собой однопетлевую поправку к действию, которая зависит от виртуальных квантов электромагнитного поля.

Формально выражение δW(1) включает в себя сумму по всем виртуальным частицам , которые могут возникнуть в фоновом поле. У нас он будет представляться в виде формального интеграла по траекториям. Так как мы будем изучать и искать излучение ,а испарение Хокинга это излучение почти черного тела ( серго тела), нам потребуется формулы для однопетлевого эффективного действия в представлении теплового ядра. В таком случае

Если  обозначает действие электромагнитного поля W, а W_E — однопетлевое
эффективное действие. тогда: exp(-W_E )  ⁼  ∫ DAe^−W , где интеграл берется
по всем возможным конфигурациям поля A. Или Z=∫DAe^−W   , где Z — это функция, описывающая вероятность того, что заданная конфигурация поля A будет реализована

Эффективное действие может быть выражено через след оператора  распространения. В однопетлевом приближении, эффективное действие W_E может быть записано в виде функционала следа оператора распространения D. Формально это выражается как:

W_E ​=−lnTrD. Здесь D — оператор распространения частицы в заданном фоновом поле. Путем взятия следа этого оператора учитываются все возможные петлевые диаграммы.

Рассмотрим стационарное рождение реальных безмассовых скалярных частиц  слабыми, электрическими и гравитационными фоновыми полями. Следуя технике Швингера [4], видно, что  соответствующая скорость неустойчивости вакуума кодируется в мнимой части однопетлевого эффективного действия, которое определяется как:

В евклидовом пространстве с метрикой g_E^μν возможна  замена переменных до лоренцевой сигнатуры в случае стационарного пространства-времени. В первой строке эффективное действие выражается через эллиптический дифференциальный оператор второго порядка для скалярного поля H. Вторая строка делает очевидной интерпретацию в терминах полевых возбуждений, локализованных в точке x(τ), которые классически развивались бы согласно H как оператор Гамильтона в течение  собственного времени s. В терминах интеграла по путям рассматриваются все траектории возбуждения, которые начинаются и заканчиваются в одной и той же точке, и взвешиваются в соответствии с классическим действием [5]: .

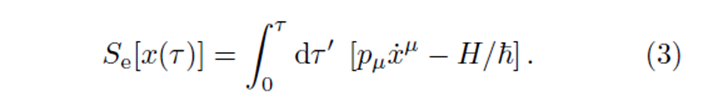
В лоренцевом аналоге замкнутая траектория требует, чтобы возбуждение поля двигалось вперед и назад во внешнем времени. Его можно интерпретировать как виртуальное рождение и уничтожение пары частица-античастица (на рис. 1 представлены светло-серыми траекториями). Сумма всех путей частица-античастица, т.е. интеграл пути в уравнении (2), называется пределом совпадения теплового ядра.   Его можно разложить на чисто классический вклад exp(−m2s) и вклад флуктуаций . Это позволяет получить мнимую часть лоренцева эффективного действия для безмассового скаляра в пределе слабого поля, в виде:

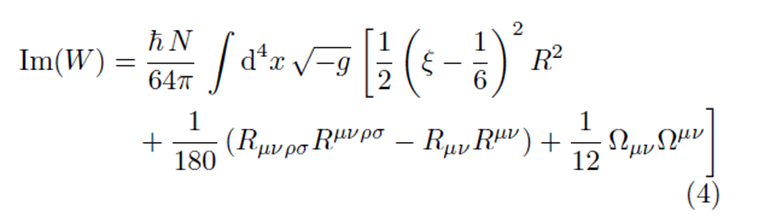
Скаляр и тензор Риччи обозначаются R и R_μν, а тензор Римана R^μνρσ . Кривизна калибровочного поля в электродинамике имеет вид  Ωμν = iqFμν/ℏ,   что дает вклад только для заряженного, то есть комплексного, скаляра. Это эффективное действие позволяет единообразно описать эффект Швингера и наш механизм образования гравитационных частиц. Уравнение (4) позволяет напрямую рассчитать эффект Швингера, т.е. плотность скоростей вакуумной неустойчивости с учетом спонтанного рождения безмассовых частиц в однородном электрическом фоновом поле в Е , а именно:

где L_eff — эффективная плотность Лагранжа, принадлежащая эффективному действию W. Этот результат согласуется с работами Эйлера, Гейзенберга  и Швингера [2] об электрон-позитронных парах при обобщении на безмассовое комплексное скалярное поле  и при обобщения на безмассовые векторные бозоны в неабелевой теории Янга–Миллса, в частности КХД

Теперь мы можем применить тот же метод к квантовому полю в искривленном пространстве-времени черной дыры. Мы рассматриваем асимптотически плоское, сферически симметричное и статическое пространство-время Шварцшильда в (3 + 1) измерениях:

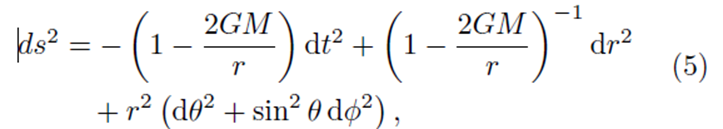
Из-за плоскостности Риччи R_μν = 0 единственный ненулевой вклад в мнимую часть
подынтегрального выражения эффективного действия (4) вносит скаляр
Кречмана   R_μνρσ

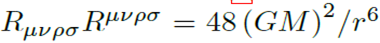
При пространственном интегрировании по внешности черной дыры, которая представляет собой область пространства-времени, причинно связанную с внешними наблюдателями,  для эффективной функции Лагранжа получается

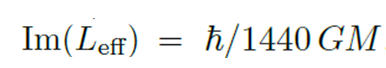
Это предсказывает плотность скорости событий образования частиц : 

где скорость относится к последующим срезам постоянного времени Шварцшильда t,  собственного времени для статического наблюдателя на бесконечности.

С помощью этого уравнения в конечном итоге и строится радиальный профиль скоростей рождаемых из гравитационного поля частиц (рис 2). Более детальное изложение можно найти в [6]

Популярное описание излучения Хокинга предполагает, что большая часть рождения частиц происходит на бесконечно малом расстоянии от горизонта событий. Для нашего механизма мы явно выводим радиальный профиль образования частиц для испаряющихся черных дыр. Его пик определяется противодействием скорости создания локальных пар и вероятность побега ( рис. 1. .

Локальное, обще ковариантное выражение для мнимой части эффективного действия в уравнении (4) фактически указывает на то, что это рождение гравитационных частиц не зависит от выбора вакуумного состояния квантового поля. Этот вывод позволяет сделать заключение, что любой массивный гравитационный объект во Вселенной будь то звезда, галактика, или туманность испаряются со временем.

Литература.

1. Joseph Polchinski  “The Black Hole Information Problem” (2016). https://arxiv.org/abs/1609.04036

2. И.Д. Новиков, В.П. Фролов “Физика черных дыр”, Москва, “Наука”, 1986.

3. J. S. Schwinger, Phys. Rev. 82, 664 (1951).

4. С Хокинг «Particle creation by black holes»   «Communications in Mathematical Physics»,1975 .

5. Matthew J. Strassler “Field Theory Without Feynman Diagrams: One-Loop Effective Actions”, 1992, https://arxiv.org/abs/hep-ph/9205205.

6. Michael F. Wondrak, Walter D. van Suijlekom, Heino Falcke “Gravitational Pair Production and Black Hole Evaporation”, 2023, https://arxiv.org/abs/2305.18521

 

 

 

Источник