Книга «Мода, вера, фантазия и новая физика Вселенной»

09.01.2020

Привет, Хаброжители! Можно ли говорить о моде, вере или фантазии в фундаментальной науке?

Вселенной не интересна человеческая мода. Науку невозможно трактовать как веру, ведь научные постулаты постоянно подвергаются строгой экспериментальной проверке и отбрасываются, как только догма начинает конфликтовать с объективной реальностью. А фантазия вообще пренебрегает и фактами, и логикой. Тем не менее великий Роджер Пенроуз не желает полностью отвергать эти феномены, ведь научная мода может оказаться двигателем прогресса, вера появляется, когда теория подтверждается реальными экспериментами, а без полета фантазии не постичь все странности нашей Вселенной.

В главе «Мода» вы узнаете о теории струн — самой модной теории последних десятилетий. «Вера» посвящена догматам, на которых стоит квантовая механика. А «Фантазия» касается ни много ни мало — теорий происхождения известной нам Вселенной.

3.4. Парадокс Большого взрыва

Сначала поставим вопрос о наблюдениях. Какие есть прямые доказательства в пользу того, что когда-то вся наблюдаемая Вселенная находилась в чрезвычайно сжатом и невероятно горячем состоянии, чтобы это согласовывалось с картиной Большого взрыва, представленной в разделе 3.1? Наиболее убедительным свидетельством является реликтовое излучение (РИ), иногда именуемое отблеском большого взрыва. Реликтовое излучение представляет собой свет, но с очень большой длиной волны, так что увидеть его глазами совершенно невозможно. Этот свет льется на нас со всех сторон исключительно равномерно (но в основном некогерентно). Он представляет собой тепловое излучение с температурой ~2,725 K, то есть на два с лишним градуса выше абсолютного нуля. Cчитается, что наблюдаемый «отблеск» зародился в невероятно горячей Вселенной (~3000 K на тот момент) примерно через 379 000 лет после Большого взрыва — в эпоху последнего рассеяния, когда Вселенная впервые стала прозрачной для электромагнитного излучения (хотя это произошло совсем не при Большом взрыве; данное событие приходится на первую 1/40 000 общего возраста Вселенной — от Большого взрыва до наших дней). С эпохи последнего рассеяния длина этих световых волн увеличилась примерно настолько, насколько расширилась и сама Вселенная (приблизительно в 1100 раз), так что плотность энергии столь же радикально уменьшилась. Поэтому наблюдаемая температура РИ составляет всего 2,725 K.

Тот факт, что это излучение существенно некогерентное (то есть тепловое), впечатляюще подтверждается самой природой его частотного спектра, приведенного на рис. 3.13. По вертикали на графике откладывается интенсивность излучения на каждой конкретной частоте, а частота возрастает слева направо. Непрерывная кривая соответствует планковскому спектру абсолютно черного тела, о котором шла речь в разделе 2.2, для температуры 2,725 K. Точки на кривой — это данные конкретных наблюдений, для которых указаны планки погрешностей. При этом планки погрешностей увеличены в 500 раз, поскольку иначе их было бы просто невозможно рассмотреть, даже справа, где ошибки достигают максимума. Совпадение между теоретической кривой и результатами наблюдений просто замечательное — пожалуй, это самое лучшее совпадение с тепловым спектром, найденное в природе.

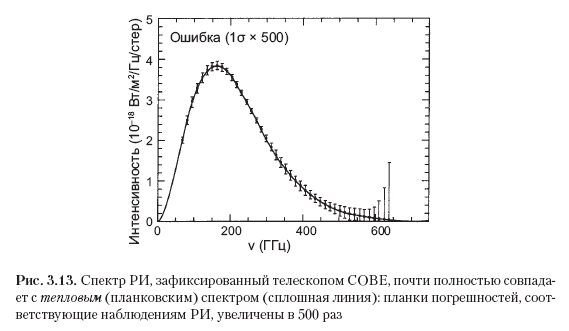
Однако о чем свидетельствует это совпадение? О том, что мы рассматриваем состояние, которое, по-видимому, находилось очень близко к термодинамическому равновесию (поэтому ранее и использовался термин некогерентный). Но какой вывод следует из того, что новоиспеченная Вселенная была очень близка к термодинамическому равновесию? Вернемся к рис. 3.12 из раздела 3.3. Самая обширная область с крупнозернистым разбиением (по определению) будет гораздо больше, чем любая другая такая область, и, как правило, она настолько велика по сравнению с остальными, что значительно превзойдет по объему их все! Термодинамическое равновесие соответствует макроскопическому состоянию, в которое, надо полагать, рано или поздно придет любая система. Иногда оно называется тепловой смертью Вселенной, но в этом случае, как ни странно, речь должна идти о тепловом рождении Вселенной. Ситуация осложняется тем, что новорожденная Вселенная стремительно расширялась, поэтому то состояние, которое мы рассматриваем, на самом деле неравновесное. Тем не менее расширение в данном случае может считаться по сути адиабатическим — данный момент в полной мере оценил Толман еще в 1934 году [Tolman, 1934]. Это означает, что величина энтропии при расширении не изменялась. (Ситуацию, подобную данной, когда благодаря адиабатическому расширению сохраняется термодинамическое равновесие, можно описать в фазовом пространстве как совокупность равных по объему областей с крупнозернистым разбиением, которые отличаются друг от друга лишь конкретными объемами Вселенной. Можно считать, что для этого первичного состояния была характерна максимальная энтропия — несмотря на расширение!).

По-видимому, мы столкнулись с исключительным парадоксом. Согласно аргументам, изложенным в разделе 3.3, Второй закон требует (и, в принципе, тем самым и объясняется), чтобы Большой взрыв был макроскопическим состоянием с крайне низкой энтропией. Однако наблюдения РИ, по-видимому, свидетельствуют о том, что макроскопическое состояние Большого взрыва отличалось колоссальной энтропией, пожалуй, даже максимально возможной. Где же мы так серьезно ошибаемся?

Вот один из распространенных вариантов объяснения этого парадокса: предполагается, что, поскольку новорожденная Вселенная была очень «маленькой», там мог существовать некий предел максимальной энтропии, и состояние термодинамического равновесия, которое, по-видимому, поддерживалось в то время, было попросту предельным уровнем энтропии, возможным на тот момент. Однако это неверный ответ. Такая картина могла бы соответствовать совершенно иной ситуации, в которой размеры Вселенной зависели бы от некоего внешнего ограничения, например, как в случае с газом, который заключен в цилиндре с герметичным поршнем. В таком случае давление поршня обеспечивается неким внешним механизмом, который оснащен внешним источником (или отводом) энергии. Но эта ситуация неприменима ко Вселенной в целом, геометрия и энергия которой, а также «габаритный размер» определяются исключительно внутренним устройством и управляются динамическими уравнениями эйнштейновской общей теории относительности (включая уравнения, описывающие состояние материи; см. разделы 3.1 и 3.2). В таких условиях (когда уравнения полностью детерминистичны и инвариантны по отношению к направлению времени — см. раздел 3.3) с течением времени не может меняться общий объем фазового пространства. При этом предполагается, что само по себе фазовое пространство P не должно «развиваться»! Вся эволюция попросту описывается расположением кривой C в пространстве P и в данном случае представляет полную эволюцию Вселенной (см. раздел 3.3).

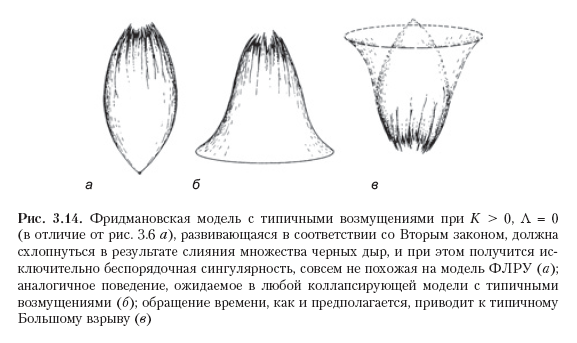
Пожалуй, проблема прояснится, если рассмотреть поздние стадии коллапса Вселенной, когда она приближается к Большому краху. Вспомните модель Фридмана при K > 0, Λ = 0, представленную на рис. 3.2 a в разделе 3.1. Теперь мы считаем, что возмущения в этой модели возникают из-за нерегулярного распределения материи, и в некоторых частях уже произошли локальные коллапсы, на месте которых остались черные дыры. Тогда следует предположить, что после этого какие-то черные дыры будут сливаться друг с другом и что схлопывание в конечную сингулярность окажется исключительно сложным процессом, не имеющим почти ничего общего со строго симметричным Большим крахом идеально шарообразной симметричной фридмановской модели, представленной на рис. 3.6 a. Напротив, в качественном отношении ситуация коллапса будет гораздо больше напоминать ту грандиозную мешанину, которая показана на рис. 3.14 a; возникающая в данном случае итоговая сингулярность может в какой-то степени согласовываться с гипотезой БКЛМ, упомянутой в конце раздела 3.2. Конечное схлопывающееся состояние будет обладать невообразимой энтропией, несмотря на то что Вселенная вновь сожмется до крохотных размеров. Хотя именно такая (пространственно-замкнутая) реколлапсирующая фридмановская модель сейчас не считается правдоподобным вариантом представления нашей собственной Вселенной, те же соображения актуальны и для других фридмановских моделей, с космологической постоянной или без нее. Коллапсирующая разновидность любой такой модели, испытывающая схожие возмущения из-за неравномерного распределения материи, опять же, должна превратиться во всепоглощающий хаос, сингулярность вроде черной дыры (рис. 3.14 б). Обратив время вспять в каждом из этих состояний, мы дойдем до возможной исходной сингулярности (потенциального Большого взрыва), имеющей, соответственно, колоссальную энтропию, что противоречит высказанному здесь предположению о «потолке» энтропии (рис. 3.14 в).

Здесь я должен перейти к альтернативным возможностям, которые также порой рассматриваются. Некоторые теоретики предполагают, что второй закон должен каким-то образом обращаться вспять в таких коллапсирующих моделях, так что общая энтропия Вселенной будет становиться все меньше (после максимального расширения) по мере приближения Большого краха. Однако такую картину особенно сложно представить себе при наличии черных дыр, которые, стоит им образоваться, сами станут работать на повышение энтропии (что связано с асимметрией времени в расположении нулевых конусов у горизонта событий, см. рис. 3.9). Это будет продолжаться и в отдаленном будущем — как минимум до тех пор, пока черные дыры не испарятся под действием хокинговского механизма (см. разделы 3.7 и 4.3). В всяком случае, подобная возможность не отменяет представленных здесь аргументов. Существует еще и другая важная проблема, которая связана с такими сложными коллапсирующими моделями и о которой, возможно, задумывались и сами читатели: сингулярности черных дыр вполне могут возникать совсем не одновременно, поэтому при обращении времени мы не получим Большой взрыв, который происходит «весь и сразу». Однако именно таково одно из свойств (пока не доказанной, но убедительной) гипотезы сильной космической цензуры [Penrose, 1998a; ПкР, раздел 28.8], согласно которой в общем случае такая сингулярность будет пространственноподобной (раздел 1.7), а потому может считаться единовременным событием. Более того, безотносительно к вопросу о справедливости самой гипотезы сильной космической цензуры известно множество решений, удовлетворяющих этому условию, и все подобные варианты (при расширении) будут обладать относительно высокими значениями энтропии. Это существенно снижает степень беспокойства относительно справедливости наших выводов.

Соответственно, мы не находим доказательств того, что при малых пространственных размерах Вселенной в ней бы обязательно существовал некий «низкий потолок» возможной энтропии. В принципе, скопление материи в виде черных дыр и слияние «чернодырных» сингулярностей в единый сингулярный хаос — это процесс, который отлично согласуется со вторым законом, и этот финальный процесс должен сопровождаться колоссальным возрастанием энтропии. «Крошечное» по геометрическим меркам окончательное состояние Вселенной может обладать невообразимой энтропией, гораздо более высокой, чем на сравнительно ранних этапах такой коллапсирующей космологической модели, и пространственная миниатюрность сама по себе не устанавливает «потолок» для максимального значения энтропии, хотя такой «потолок» (при обращении хода времени) как раз мог бы объяснить, почему при Большом взрыве энтропия была чрезвычайно мала. На самом деле такая картина (рис. 3.14 a, б), на которой в общем виде представлен коллапс Вселенной, подсказывает разгадку парадокса: почему при Большом взрыве была исключительно низкая энтропия по сравнению с той, что могла быть, несмотря на то что взрыв был горячим (а такое состояние должно обладать максимальной энтропией). Ответ заключается в том, что энтропия может радикально увеличиваться, если допустить серьезные отклонения от пространственной однородности, и величайший прирост такого рода связан с неравномерностями, обусловленными как раз возникновением черных дыр. Следовательно, пространственно-однородный Большой взрыв действительно мог обладать, условно говоря, неимоверно низкой энтропией, несмотря на то что его содержимое было невероятно горячим.

Одно из наиболее убедительных доказательств в пользу того, что Большой взрыв действительно был довольно однородным с пространственной точки зрения, хорошо согласующееся с геометрией модели ФЛРУ (но не согласующееся с гораздо более общим случаем беспорядочной сингулярности, проиллюстрированным на рис. 3.14 в), вновь связано с РИ, но на этот раз с его угловой однородностью, а не с термодинамической природой. Такая однородность проявляется в том, что температура РИ практически одна и та же в любой точке неба, и отклонения от однородности составляют не более 10–5 (с поправкой на небольшой доплеровский эффект, связанный с нашим движением сквозь окружающую материю). Кроме того, наблюдается практически всеобщая однородность в распределении галактик и другой материи; так, распределение барионов (см. раздел 1.3) в достаточно больших масштабах характеризуется значительной однородностью, хотя и есть заметные аномалии, в частности так называемые войды, где плотность видимой материи кардинально ниже среднего. В целом можно утверждать, что однородность оказывается тем выше, чем дальше в прошлое Вселенной мы заглядываем, а РИ — это древнейшее свидетельство распределения материи, которое мы можем непосредственно наблюдать.

Эта картина согласуется с точкой зрения, согласно которой на ранних этапах развития Вселенная действительно была исключительно однородной, но со слегка нерегулярной плотностью. С течением времени (и под влиянием различного рода «трения» — процессов, замедляющих относительные движения) эти плотностные неравномерности усиливались под действием гравитации, что согласуется с представлением о постепенном комковании вещества. Со временем комкование нарастает, в результате образуются звезды; они группируются в галактики, в центре каждой из которых образуется массивная черная дыра. В конечном итоге такое комкование обусловлено неотвратимым действием гравитации. Такие процессы действительно сопряжены с сильнейшим нарастанием энтропии и демонстрируют, что с учетом гравитации тот первозданный сияющий шар, от которого сегодня осталось лишь РИ, мог обладать далеко не максимальной энтропией. Термическая природа этого шара, о которой свидетельствует планковский спектр, показанный на рис. 3.13, говорит лишь вот о чем: если рассмотреть Вселенную (в эпоху последнего рассеяния) просто как систему, состоящую из вещества и энергии, взаимодействующих друг с другом, то можно считать, что она фактически находилась в термодинамическом равновесии. Однако если при этом учесть и гравитационные воздействия, то картина драматическим образом меняется.

Если представить себе, например, газ в герметичном контейнере, то естественно считать, что максимальной энтропии он достигнет в том макроскопическом состоянии, когда равномерно распределится по всему контейнеру (рис. 3.15 a). В данном отношении он будет напоминать раскаленный шар, породивший РИ, которое равномерно распределено по небу. Однако если заменить молекулы газа обширной системой тел, связанных друг с другом гравитацией, например отдельных звезд, то получится совершенно иная картина (рис. 3.15 б). Из-за гравитационных эффектов звезды распределятся неравномерно, в виде скоплений. В конечном итоге наибольшая энтропия будет достигнута, когда многочисленные звезды сколлапсируют или сольются в черные дыры. Несмотря на то что на этот процесс и может потребоваться немало времени (хотя ему и будет способствовать трение, обусловленное присутствием межзвездного газа), мы увидим, что в конечном итоге при доминировании гравитации энтропия тем выше, чем менее равномерно распределено вещество в системе.

Такие эффекты прослеживаются даже на уровне повседневного опыта. Возможен вопрос: а какова роль Второго закона в поддержании жизни на Земле? Часто можно услышать, что мы живем на этой планете благодаря энергии, получаемой от Солнца. Но это не вполне верное утверждение, если рассматривать Землю в целом, так как практически вся энергия, получаемая Землей днем, вскоре вновь улетучивается в космос, в темное ночное небо. (Разумеется, точный баланс будет немного корректироваться под влиянием таких факторов, как глобальное потепление и разогрев планеты под действием радиоактивного распада.) В противном случае Земля попросту раскалялась бы все сильнее и за несколько дней стала бы необитаемой! Однако фотоны, получаемые непосредственно от Солнца, обладают относительно высокой частотой (они сосредоточены в желтой части спектра), а Земля отдает в космос гораздо более низкочастотные фотоны, относящиеся к инфракрасному спектру. По формуле Планка (E = hν, см. раздел 2.2) каждый из поступающих от Солнца фотонов в отдельности обладает гораздо более высокой энергией, чем фотоны, излучаемые в космос, поэтому для достижения баланса с Земли должно уходить гораздо больше фотонов, чем приходит (см. рис. 3.16). Если поступает меньше фотонов, то у входящей энергии будет меньше степеней свободы, а у исходящей — больше, и, следовательно, по формуле Больцмана (S = k log V) входящие фотоны будут обладать гораздо меньшей энтропией, чем исходящие. Мы пользуемся низкоэнтропийной энергией, заключенной в растениях, чтобы понижать собственную энтропию: едим растения либо травоядных животных. Так жизнь на Земле сохраняется и процветает. (По-видимому, эти мысли впервые четко сформулировал Эрвин Шрёдингер в 1967 году, написавший свою революционную книгу «Жизнь как она есть» [Schrödinger, 2012]).

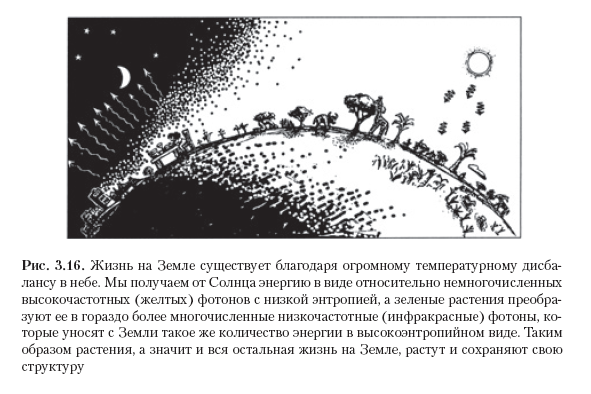
Важнейший факт, связанный с этим низкоэнтропийным балансом, заключается в следующем: Солнце — это горячее пятно в совершенно темном небе. Но как сложились такие условия? Сыграли роль многие сложные процессы, в том числе связанные с термоядерными реакциями и т. д., но самое важное то, что Солнце вообще существует. А оно возникло потому, что солнечная материя (как и материя, образующая другие звезды) развивалась в процессе гравитационного комкования, причем все начиналось с относительно однородного распределения газа и темной материи.

Здесь требуется упомянуть загадочную субстанцию под названием темная материя, которая, по-видимому, составляет 85 % материального (не-Λ) содержимого Вселенной, но она обнаруживается только по гравитационному взаимодействию, а состав ее неизвестен. Сегодня мы всего лишь учитываем эту материю при оценке общей массы, которая нужна при расчете некоторых числовых величин (см. разделы 3.6, 3.7, 3.9, а о том, какую более важную теоретическую роль может играть темная материя, см. раздел 4.3). Безотносительно к проблеме темной материи мы видим, насколько важной для нашей жизни оказалась низкоэнтропийная природа первоначального однородного распределения материи. Наше существование, насколько мы его понимаем, зависит от низкоэнтропийного гравитационного запаса, который характерен для исходного однородного распределения материи.

Здесь мы подходим к примечательному — на самом деле даже фантастическому — аспекту Большого взрыва. Тайна кроется не только в том, как он произошел, но и в том, что это было событие с чрезвычайно низкой энтропией. Более того, примечательно не столько это обстоятельство, сколько сам факт, что энтропия была низкой лишь в одном конкретном отношении, а именно: гравитационные степени свободы по какой-то причине были полностью подавлены. Это резко контрастирует со степенями свободы материи и (электромагнитного) излучения, поскольку они, по-видимому, были максимально возбуждены в горячем состоянии с максимальной энтропией. На мой взгляд, это, пожалуй, глубочайшая космологическая загадка, и по какой-то причине она до сих пор остается недооцененной!

Следует подробнее остановиться на том, сколь особенным было состояние Большого взрыва и какая энтропия может возникнуть в процессе гравитационного комкования. Соответственно, нужно для начала осознать, какая невероятная энтропия на самом деле присуща черной дыре (см. рис. 3.15 б). Этот вопрос мы обсудим в разделе 3.6. Но пока давайте обратимся к другой проблеме, связанной со следующей, довольно вероятной возможностью: ведь Вселенная на самом деле может оказаться пространственно-бесконечной (как в случае ФЛРУ-моделей с K 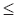0, см. раздел 3.1) или как минимум большая часть Вселенной может быть недоступна для непосредственного наблюдения. Соответственно, мы подходим к проблеме космологических горизонтов, о которой поговорим в следующем разделе.