На первый взгляд, особенно если смотреть на мультяшную версию атома, описанную мною ранее со всеми её недостатками, электроны, двигающиеся по орбите вокруг ядра, выглядят так же, как планеты, двигающиеся по орбите вокруг Солнца. И вроде бы принцип этих процессов одинаков. Но есть подвох.
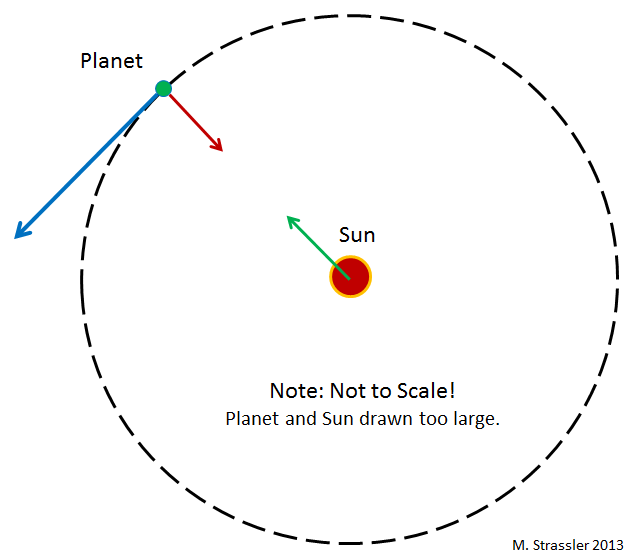
Рис 1
Что удерживает планеты на орбите вокруг Солнца? В Ньютоновской гравитации (Эйнштейновская сложнее, но тут она нам не нужна) любая пара объектов притягивается друг к другу посредством гравитационного взаимодействия, пропорционального произведению их масс. В частности, гравитация Солнца притягивает к нему планеты (с силой, обратно пропорциональной квадрату расстояния между ними. То есть, если расстояние уменьшается вдвое, сила увеличивается вчетверо). Планеты тоже притягивают Солнце, но оно настолько тяжёлое, что это почти не влияет на его движение.
Инерция, тенденция объектов к перемещению по прямым линиям в случае отсутствия действия на них других сил, работает против гравитационного притяжения, и в результате планеты двигаются вокруг Солнца. Это видно на рис.1, где изображена круговая орбита. Обычно эти орбиты эллиптические – хотя в случае планет они почти круглые, поскольку так формировалась Солнечная система. Для различных мелких камней (астероидов) и глыб льда (комет), двигающихся по орбитам вокруг Солнца, это уже не так.
Сходным образом все пары электрически заряженных объектов притягиваются или отталкиваются друг от друга, с силой, тоже обратно пропорциональной квадрату расстояния между ними. Но, в отличие от гравитации, которая всегда притягивает объекты вместе, электрические силы могут как притягивать, так и отталкивать. Объекты, обладающие одинаковыми, положительными или отрицательными зарядами, отталкиваются. А отрицательно заряженный объект притягивает положительно заряженный объект, и наоборот. Отсюда и романтическая фраза «противоположности притягиваются».
Поэтому положительно заряженное атомное ядро в центре атома притягивает легковесные электроны, двигающиеся на задворках атома, к себе, примерно как Солнце притягивает планеты. Электроны тоже притягивают ядро, но масса ядер настолько больше, что их притяжение почти не влияет на ядро. Электроны также отталкиваются друг от друга, что является одной из причин, по которым они не любят проводить время близко друг к другу. Можно было бы считать, что электроны в атоме перемещаются по орбитам вокруг ядра примерно так же, как планеты перемещаются вокруг Солнца. И на первый взгляд, именно так они и поступают, особенно в мультяшном атоме.
Но вот, в чём подвох: на самом деле, это двойной подвох, и каждый из двух подвохов оказывает эффект, противоположный другому, в результате чего они взаимно уничтожаются!
Двойной подвох: как атомы отличаются от планетных систем
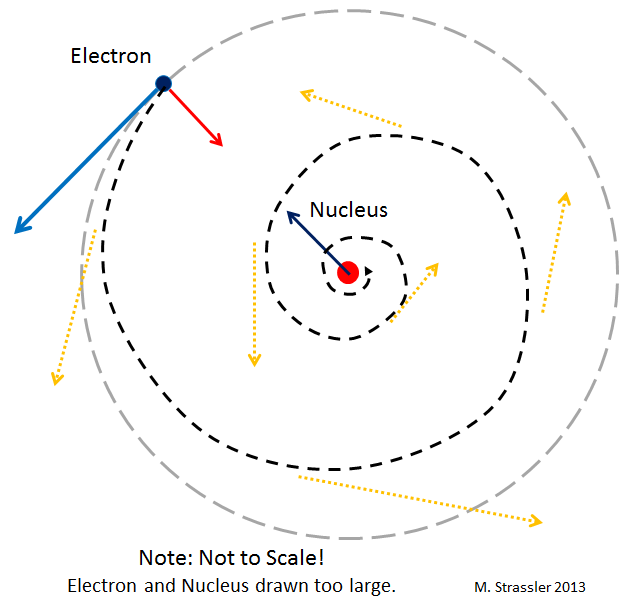
Рис 2
Первый подвох: в отличие от планет, электроны, двигающиеся по орбитам вокруг ядра, должны излучать свет (точнее, электромагнитные волны, одним из примеров которых служит свет). А это излучение должно заставлять электроны замедляться и по спирали падать на ядро. В принципе, в теории Эйнштейна существует схожий эффект – планеты могут испускать гравитационные волны. Но он чрезвычайно мал. В отличие от случая с электронами. Получается, что электроны в атоме должны очень быстро, за малую долю секунды, по спирали упасть на ядро!
И они бы так и сделали, если бы не квантовая механика. Потенциальная катастрофа изображена на рис. 2.
Второй подвох: но наш мир работает согласно принципам квантовой механики! А у неё есть свой удивительный и контринтуитивный принцип неопределённости. Этот принцип, описывающий тот факт, что электроны – это такие же волны, как и частицы, заслуживает своей собственной статьи. Но вот, что нам нужно знать о нём для сегодняшней статьи. Общее следствие этого принципа состоит в том, что невозможно знать все характеристики объекта одновременно. Существуют наборы характеристик, для которых измерение одной из них делает другие неопределёнными. Один из случаев – это местоположение и скорость таких частиц, как электроны. Если вы точно знаете, где находится электрон, вы не знаете, куда он направляется, и наоборот. Можно достичь компромисса и с некоторой точностью знать, где он, и с некоторой точностью знать, куда он направляется. В атоме так всё и получается.
Допустим, электрон по спирали падает на ядро, как на рис. 2. В процессе его падения нам всё точнее и точнее будет известно его местоположение. Тогда принцип неопределённости говорит нам, что его скорость будет становиться всё более и более неопределённой. Но если электрон остановится на ядре, его скорость не будет неопределённой! Поэтому он не может остановиться. Если он вдруг попробует упасть вниз по спирали, ему придётся всё быстрее и быстрее передвигаться случайным образом. И это увеличение скорости уведёт электрон в сторону от ядра!
Так что тенденция падения по спирали будет нейтрализована тенденцией к более быстрому движению согласно принципу неопределённости. Баланс находится, когда электрон располагается на предпочтительном расстоянии от ядра, и это расстояние определяет размер атомов!

Рис 3
Если электрон изначально находится далеко от ядра, он будет двигаться к нему по спирали, как показано на рис. 2, и излучать электромагнитные волны. Но в результате его расстояние от ядра станет достаточно малым для того, чтобы принцип неопределённости запретил дальнейшее сближение. На этом этапе, когда найден баланс между излучением и неопределённостью, электрон организует стабильную «орбиту» вокруг ядра (точнее, орбиталь – этот термин выбран, чтобы подчеркнуть, что в отличие от планет, у электрона из-за квантовой механики нет таких орбит, какие есть у планет). Радиус орбитали определяет радиус атома (рис. 3).
Ещё одна особенность – принадлежность электронов к фермионам – заставляет электроны не спускаться до одного радиуса, и выстраиваться по орбиталям разных радиусов.
Насколько атомы крупные? Приближение на основе принципа неопределённости
На самом деле мы можем примерно оценить размер атома, используя только расчёты для электромагнитных взаимодействий, массу электрона и принцип неопределённости. Для простоты проделаем расчёты для атома водорода, где ядро состоит из одного протона, вокруг которого двигается один электрон.
- Массу электрона обозначим
- Неопределённость позиции электрона обозначим Δx
- Неопределённость скорости электрона обозначим Δv
Принцип неопределённости утверждает:
где ℏ — это постоянная Планка h, делённая на 2 π. Обратите внимание, он говорит, что (Δ v) (Δ x) не может быть слишком малым, что означает, что обе определённости не могут быть слишком малыми, хотя одна из них может быть очень малой, если другая будет очень большой.
Когда атом устанавливается в предпочтительном основном состоянии, мы можем ожидать, что знак ≥ превратится в знак ~, где A ~ B означает, что «A и B не совсем равны, но и не сильно отличаются». Это очень полезный символ для оценок!
Для атома водорода в основном состоянии, в котором неопределённость положения Δx будет примерно равна радиусу атома R, а неопределённость скорости Δv будет примерно равна типичной скорости V движения электрона вокруг атома, мы получим:
Как узнать R и V? Между ними и силой, удерживающей атом вместе, существует взаимоотношение. В неквантовой физике объект массы m, находящийся на круговой орбите радиуса r, и двигающийся со скоростью v вокруг центрального объекта, притягивающего его с силой F, будет удовлетворять уравнению
К электрону в атоме напрямую это неприменимо, но приближённо это работает. Сила, действующая в атоме, это электрическая сила, с которой протон с зарядом +1 притягивает электрон с зарядом -1, и в результате уравнение принимает вид
где k – константа Кулона, e – единица заряда, c – скорость света, ℏ — это постоянная Планка h, делённая на 2 π, а α – определённая нами постоянная тонкой структуры, равная . Совместим два предыдущих уравнения для F, и оценочное соотношение получается следующим:
Теперь применим это к атому, где v → V, r → R, и m → me. Также умножим верхнее уравнение на . Это даёт:
На последнем шаге мы использовали наше соотношение неопределённости для атома, . Теперь можно вычислить радиус атома R:
И это оказывается практически точным! Такие простые оценки не дадут вам точных ответов, но очень хорошее приближение обеспечат!
Источник


