Теория струн
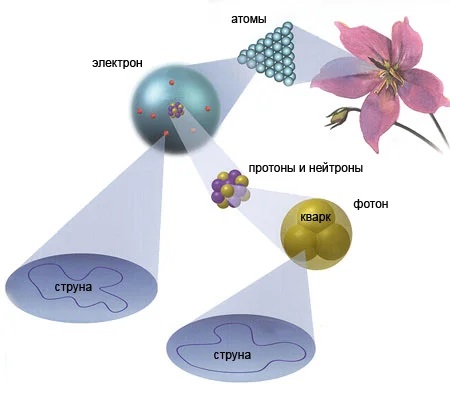
На хабре уже была статья по теории струн. Если вкратце в 1968 году ученые обратили внимание, что математическая функция, которая называется бета-функция Эйлера, идеально описывает свойства частиц, которые участвуют в так называемом сильном взаимодействии — одном из четырёх фундаментальных взаимодействий во Вселенной.
При дальнейших проверках этот факт получил подтверждение, интересно было и то, что ранее данная функция в основном применялась при описании колебаний натянутых струн.
При виде всего этого исследователи задались резонным вопросом «А что, если элементарные частицы вовсе и не частицы, а микроскопические тончайшие струны, а то, что мы наблюдаем на практике — это не траектория движения частицы, а траектория колебания, проходящего по этой струне?».
Первые же исследования показали, что теория струн достигает значительных успехов в описании наблюдаемых явлений. Не без оснований казалось, что теория струн, способна свести все четыре фундаментальных взаимодействия Вселенной к одному — колебанию одномерной струны с соответствующим переносом энергии. При этом теория струн так же позволяет объяснить основные константы микромира с математической точки зрения. Становилось понятно, почему, например, массы элементарных частиц именно такие, какие есть.
Кроме того, теория струн давала надежду на объединение ОТО (общая теория относительности) и квантовой механики в рамках одной теории. При расчётах выяснилось, что собственные колебания струн способны гасить и уравновешивать квантовые флуктуации и тем самым устранить возмущения на микроскопическом уровне, из-за которых ОТО и квантовую механику никак не удавалось подружить.
Однако, при более глубоких исследованиях и проверках теории выявились серьёзные противоречия следствий с экспериментальными данными. Например, в теории струн обязательно присутствовала частица, тахион (квадрат массы которой был меньше нуля) в качестве основного состояния струны, что подразумевало под собой нестабильное состояние струны и явно показывало, что теория струн требует модификации.
Теория суперструн
В 1971 году была создана модифицированная теория струн под названием «теория суперструн».
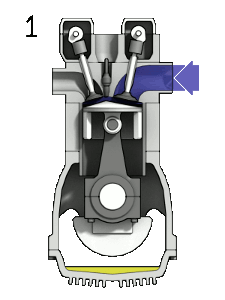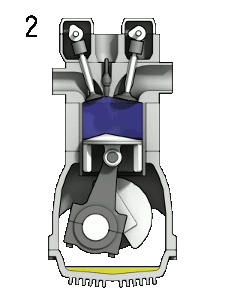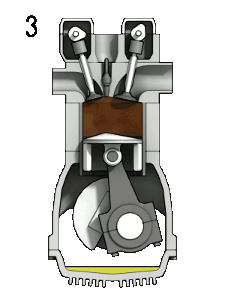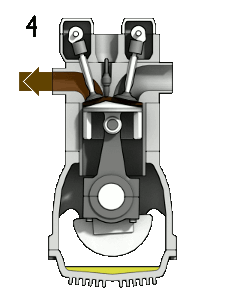
Для понимания модификаций попробуем разобраться с такой характеристикой, как спин. Имеется распространенный вариант объяснения сути спина «на пальцах»: спин — это количество оборотов вокруг своей оси, которые надо сделать частице, чтобы выглядеть так же, как вначале. Для спинов в пределах единицы все вроде понятно (любому предмету неправильной формы можно приписать «спин», равный единице), а для попытки представить себе форму объекта, который надо прокрутить вокруг оси дважды, чтобы он выглядел так же, как вначале, можно посмотреть на иллюстрацию справа. На ней изображен четырёхтактный двигатель, который возвращается в исходное состояние при повороте коленчатого вала на 720°, что является неким аналогом полуцелого спина.
На данный момент считается, что элементарные частицы могут иметь только полуцелый или целочисленный спины. Бозонами называются те частицы, которые имеют целочисленный спин. Фермионы — частицы, у которых спин полуцелый. Исходя из этого, первая версия теории струн описывала только бозоны, из-за чего она также называлась как «бозонная теория струн». Теория суперструн же включала и фермионы — при таком подходе проблема наличия тахионов, как и множество других противоречий в теории разрешались!
Но не обошлось без новых проблем. В теории суперструн получалось, что для каждого бозона должен существовать соответствующий фермион, то есть между бозонами и фермионами должна существовать определённая симметрия. Такой вид симметрии предсказывался и раньше — под названием «суперсимметрия». Но экпериментально существование суперсимметричных фермионов не было подтверждено. Объяснялось это тем, что по расчётам, суперсимметричные фермионы должны обладать огромной для микромира массой, и потому в обычных условиях их не получить. Для того, чтобы зарегистрировать их, нужны огромные энергии, которые достигаются при столкновении лёгких частиц на почти световых скоростях.
Суперсимметричные фермионы и сейчас пытаются зарегистрировать в экспериментах на Большом адронном коллайдере, но пока безуспешно.
Многомерная Вселенная
В то же время уравнения теории суперструн никак не хотели согласовываться с квантовой теорией, выдавая в результате отрицательные или бо́льше единицы вероятности.
Чтобы были понятны предпосылки дальнейшего развития теории, совершим небольшой экскурс в историю. В далёком 1919 году немецкий математик Калуца прислал Эйнштейну письмо, где изложил свою теорию в которой делал допущение, что на самом деле Вселенная может быть четырёхмерной в пространстве, и в доказательство своих слов приводил свои расчёты, из которых получалось, что при таком условии ОТО замечательно согласовывается с теорией электромагнитного поля Максвелла, чего невозможно достичь в обычной трехмерной Вселенной. Современники высмеяли теорию, вскоре и Эйнштейн, изначально заинтересовавшийся теорией, разочаровался в ней.
В 1926 году физик Оскар Клейн тоже заинтересовался работами Калуцы и усовершенствовал его модель. По Клейну получалось, что дополнительное измерение действительно может существовать, но оно находится в «свёрнутом» и зацикленном на самом себе виде. Причём свернуто четвёртое измерение очень туго — до размеров элементарных частиц, поэтому мы его и не замечаем. Теория получила название пятимерного мира Калуцы — Клейна (четыре измерения в пространстве + время), но и она пробыла в забвении вплоть до 80-х годов 20 века.
Ученые в попытке объяснить несоответствия теории струн с квантовой механикой выдвинули предположение, что проблемы в расчётах были из-за того, что струны в нашей теории могут колебаться всего лишь в трёх направлениях, которыми располагает наша Вселенная. Вот если бы струны могли бы колебаться в четырёх измерениях…
Расчёты показали, что и в этом случае проблемы остаются, но зато число противоречия в уравнениях уменьшаются. Исследователи продолжали увеличивать число измерений, пока не ввели целых 9 измерений в пространстве, при которых, наконец-то, теория суперструн сошлась с квантовой механикой и ОТО. Этот момент вошел в историю как «первая революция в теории струн». Именно с этого момента начали раздаваться возгласы, что на самом деле мы живём в десятимерной Вселенной — одно измерение во времени, три знакомых нам измерения развернуты до космических размеров, а остальные шесть свернуты в микроскопических масштабах и потому незаметны.
С практической точки зрения ни подтвердить, ни опровергнуть экспериментально это на данный момент невозможно, так как речь идёт о таких малых масштабах струн и свернутых измерений, которые недоступны для фиксации современной аппаратурой.

При дальнейших разработках ученым удалось в теории установить общий вид шести свернутых измерений, при которых наш мир оставался таким, какой он есть. Этот вид соответствует математическим объектам из группы под названием «многообразия Калаби-Яу» (на илл. справа). Но каких-то многообещающих следствий это не принесло, хотя общий вид этих объектов и вычислили, но точный вид, как оказалось, нельзя установить без эксперимента. А без нахождения точного вида пространства Калаби-Яу нашей Вселенной вся теория суперструн сводилась по сути в гадание на кофейной гуще.

Впрочем, работы продолжались, и постепенно ученым удалось вычленить из общей массы гипотез пять более-менее правдоподобных теорий, которые могли бы описать нашу Вселенную. Это 5 известных суперструнных теорий, при этом все они ра́вно претендовали на звание единственно верной и при этом выглядели несовместимыми между собой, что вызывало у ученых сильную обеспокоенность.
М-теория
Лишь в середине девяностых годов прошлого века произошла так называемая «вторая революция в теории струн». Эдвард Виттен выдвинул гипотезу, что различные суперструнные теории представляют собой различные предельные случаи неразработанной пока 11-мерной М-теории.

Введение ещё одного измерения в целом не нарушает связь квантовой теории и ОТО, и более того — снимает очень многие накопившиеся проблемы в теории суперструн. В том числе успешно скрещивает все пять суперструнных теорий в одну-единственную M-теорию, которая на сегодня является без преувеличения высшим достижением физиков в деле познания Вселенной.
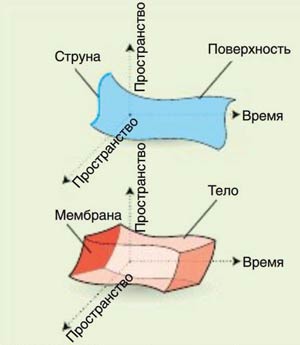
Согласно M-теории получается, что основа Вселенной — не только одномерные струны. Могут существовать и двухмерные аналоги струн — мембраны, и трёхмерные, и четырёхмерные… Эти конструкции были названы бранами (струна — 1-брана, мембрана — 2-брана, и так далее). М-теория оперирует двумерными и пятимерными бранами, но даже базовая теория бран на данный момент все ещё находится в разработке. Существование бран экспериментально не подтверждено — на данном этапе развития теории считается, что браны принципиально ненаблюдаемы.
При всем при этом М-теория при низких энергиях аппроксимируется супергравитацией в одиннадцати измерениях. Связь с гравитацией делает М-теорию претендентом на то, чтобы стать связующей теорией между всеми фундаментальных взаимодействий во Вселенной, или другими словами — «Единой теорией всего».
Однако, проблема с конечным видом пространства Калаби-Яу в М-теории всё ещё остается нерешенной — на макроскопических масштабах теория должна сводиться к известной и очень хорошо проверенной физике элементарных частиц. Но, как выясняется, способов такого сведения существует по меньшей мере 10100, а то и 10500, а то и вовсе бесконечность. При этом каждая из получившихся четырёхмерных теорий описывает свой собственный мир, который может быть похож на реальность, а может и принципиально отличаться от неё.
Всё это из-за того, что свойства частиц считаются способом колебания струн, а возможные способы колебания струн зависят от точной геометрии дополнительных измерений. Существующим приближенным уравнениям удовлетворяет огромное количество разных геометрий. То есть эти уравнения были бы справедливы не только в нашем мире, но и в огромном количестве других миров, а возможно — в любом мире. Будь эти приближенные уравнения окончательными, теорию можно было бы признать нефальсифицируемой по Попперу, то есть ненаучной теорией. А так — нахождение точных уравнений, возможно, всё ещё расставит по своим местам.
В данный момент развитие М-теории осложняется еще и тем, что уравнения её описывающие настолько сложны, что ученые большей частью оперируют только их приближёнными формами, что не ведёт к повышению точности результатов. Более того, часто складывается такая ситуация, что для решения этих уравнений даже соответствующих математических методов не создано, что также создает существенные проблемы. В последнее время там где физика упирается в тупик, на самом деле часто в тупик упирается именно математика. Некоторые ученые говорят, что заметное развитие М-теория получит, только если случится «математический прорыв».
Теория струн и, в частности, М-теория, сегодня является одним из самых динамично развивающихся направлений современной физики. И хотя часть ученых из-за фундаментальных проблем довольно скептически относится к тому, что данная теория в конце концов приведет к физической теории, описывающей наш реальный мир. Существенная часть исследователей не оставляет своих надежд и верит, что в один прекрасный день М-теория таки оформится в элегантную и математически изящную Единую теорию всего.
Надеюсь, что данная статья не оставила Вас равнодушными, и буду очень рад если Вы решите, что не зря потратили время за чтением.


