[Из песочницы] Споривное собеседование

Совсем недавно проходил собеседование в одной уважаемой компании. Дали несколько десятков логических задач. Справился без особого труда, но времени было в обрез. Проверяющий с усмешкой посмотрел на меня: «Вы не справились с простой задачей». Честно, мне стало не по себе.

А вот та самая задача:

Саша и Вася бегут 100 метровку. Когда Саша финиширует, Вася пробегает лишь 90 метров.
Во втором забеге бегут также, только Саша стартует, когда Вася пробегает первые 10 метров.
Кто финиширует первый?

Вроде классическая задача из задачника 7-9 класса. Далее лучше читать, если есть ответ.
Отвечал я интуитивно, особо не задумываясь, была всего минута – «Вася». Возможно у вас противоположный ответ.

Вася и Саша окажутся на отметке 90 метров одновременно (следует из первого забега + учитывая фору в 10 метров). А оставшиеся 10 метров… — Саша быстрее

— вот и весь ответ. Красивое решение, не правда ли?! Я до этого не додумался.

Я бегал на спринтерские дистанции и интуитивно понимал, что 10 метров отыграть нереально. Я знал кинематику 100 метрового забега, что и явилось спасательным кругом. Я был не согласен с таким решением. Попросил 10 мин, чтобы смог обосновать свой ответ. «Ну, давай», — услышал я.

В условии задачи ничего не говорится о характере движения. Соответственно, характер движения возьмем наиболее близкий к реальному. Ниже представлена диаграмма скорости по мере прохождения дистанции.

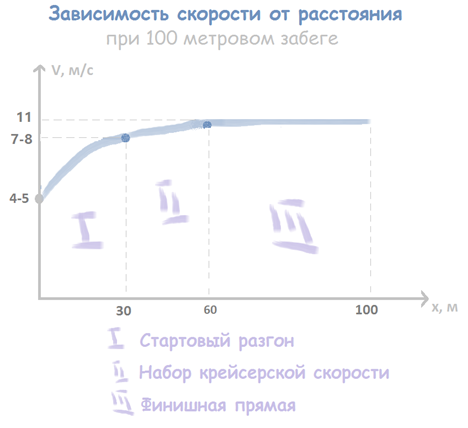
Для простоты возьмем упрощенную модель. Будем считать, что до момента t0 спортсмены набирают скорость линейно, а далее, скорость постоянна. Также, оба спортсмена имеют одинаковую начальную скорость и время разгона.

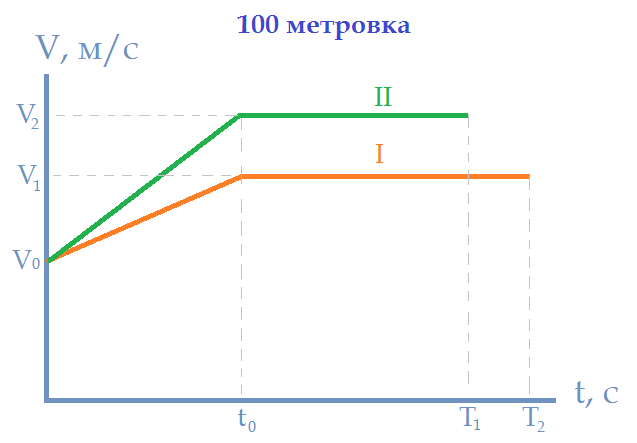
Теперь зафиксируем ряд переменных, чтобы численно решить задачу. Берем сразу диапазоны, чтобы рассмотреть различные категории спортсменов:

1. Мгновенная начальная скорость V0, возьмем от 3-5 м/с, где 3 м/c – студенты, 4 – профи, 5 – чемпионы;
2. Разгонное время t0, на мировых первенствах это ~5 с, у студентов меньше. Возьмем диапазон от 3-х до 5-ти секунд;
3. Максимальная скорость V2, возьмем 8 — 10 м/c, где 10 м/с – уровень ЧМ.

Этого достаточно, чтобы решить задачу полностью. Поехали.

Из первого забега получаем связь максимальных скоростей спортсменов (I) и время T1 и T2, за которые спортсмены пробегают 100 метров (II — III):

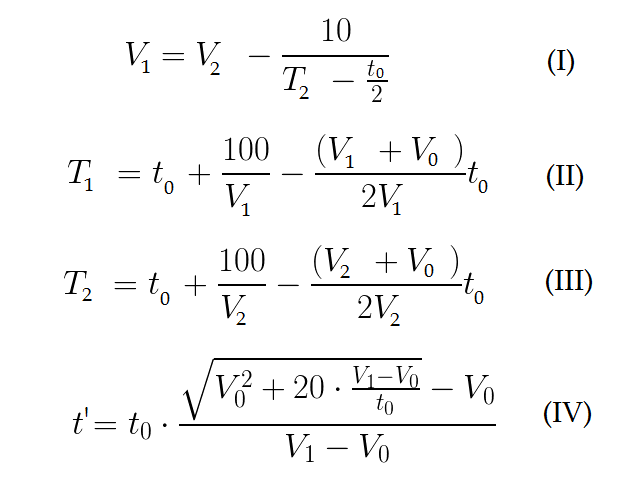
Во втором забеге T1 и T2 будут такими же (по условию), но второй спортсмен стартует с задержкой t`. Таким образом, если T1 — T2 > t`, то второй спортсмен (Саша) снова выиграет. t` – это время, за которое Вася пробежит первые 10 метров (IV).

Ну вот, подставляем различные комбинации начальных параметров и смотрим на результат (T, c – отставание Саши на финише в секундах, X, м – отставание в метрах):

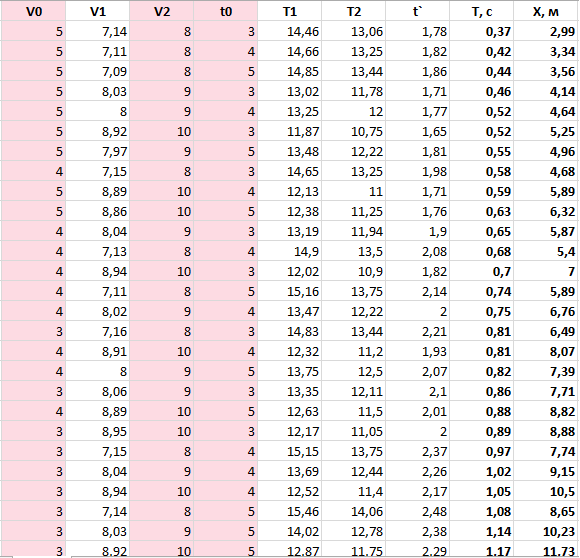
Таблица отсортирована по времени отставания. Как видим, во всех рассмотренных нами случаях Саша прибегает вторым. Даже есть случаи, когда начальная фора в 10 м увеличивается. Таким образом, в нашей модели, которая максимально приближена к реальному, у Саши микроскопическая вероятность на победу. Модель «постоянной скорости» хорошее упрощение во многих задачах, но тут именно тот случай, когда это приводит нас к противоположному результату.

В заключение скажу, что ответ не есть самое главное. Важна адекватная модель и ход ваших мыслей.

P.S. За такую «неправильно» решенную задачу получил большой жирный плюс.