Исследование операций

Cодержание

1. Введение

2. Основные понятия и термины

3. Характеристика ИО как научной дисциплины

4. Этапы операционного исследования

   • Постановка задачи

   • Построение математической модели

   • Нахождение решения с помощью математической модели

   • Проверка модели и решения

   • Построение процедуры подстройки и решения

   • Осуществление решения

5. Предметные процессы ИО и задачи

   • Процессы обслуживания

   • Распределения

   • Управления запасами

   • Замены

   • Состязательные

6. Модели процессов ИО и их логическая структура

   • Постановка задачи

   • Элементы задачи ИО

   • Взаимодействие исполнения и управления при ИО

7. Литература

Введение

При функционировании больших сложно устроенных систем в них, как правило, протекают многообразные процессы, сущность которых состоит в различного рода преобразованиях физико-химической субстанции из сырья в конечный продукт, поставляемый на рынок. Наряду с материальной субстанцией в производственных процессах широко используется информация управленческая и технологическая. Когда-то не в столь давние времена достаточно сложным механизмом, системой считался часовой механизм, реализуемый зацеплением шестеренок. Механизм преобразовывал временную субстанцию в информацию. Выходным продуктом такого механизма была информация — сведения о текущем временном моменте, к точности которой уже в те времена предъявлялись жесткие требования. Все процессы сложных производственных систем также, подобно механизму часов, постоянно должны быть в «зацеплении», тесно взаимодействовать, протекать синхронно и согласованно. Главным требованием к такой системе с шестеренками была точность отсчетов временных промежутков. И сегодня точность нужна везде от водных, наземных, воздушных транспортных систем до спутниковых космических, атомных энергетических станций. Исследуя операции, следует помнить об истории их появления и проявления в различных отраслях хозяйства и производства.

Начнем с рассмотрения типичной простой и понятной задачи. Пусть в пределах населенного пункта в точках (х₀, х₁) имеется n складов с товарами. На каждом складе припаркован под погрузку автоприцеп, который загружается товарами. В других точках (х₀, х₁) района (окрестности населенного пункта) размещаются заказчики (потребители товаров), которым необходимо эти товары доставить. В n точках (х₀, х₁) размещены n тягачей, которые должны доставить заказчикам загруженные товарами по их заявкам автоприцепы. Такая доставка связана с расходом топлива, с затратами времени и многими другими явлениями и событиями.

Владелец транспортных средств располагает матрицей:

стоимости (затрат) топлива в операции перевозки.

Очевидно, что в операции желательно ограничить расход топлива при условии выполнения доставки товаров всем заказчикам. Математическая модель затрат представляется простой линейной формой:

Это соотношение называют целевой функцией (ЦФ). Неизвестными здесь являются переменные (x_ij) , т.е. куда тягач с номером (i) должен доставить груженый прицеп с номером (j). Ясно, что суммарные затраты будут определяться планом Х[i, j] перевозок или выбором переменных (x_ij)  в совокупности. Постоянно будем иметь ввиду очевидное ограничивающее условие: один тягач везет один прицеп, каждый прицеп обслуживается одним тягачом. Из этого условия следует, что каждый элемент (x_ij), выбираемый для подстановки в  ЦФ, не может быть дробным значением, а принимает одно из значений 0 или 1, т.е. (x_ij ≥0, i = 1(1)n, j = 1(1)n).  Приведенное выше условие интерпретируется в модели как ограничения, накладываемые на переменные (x_ij).

(i = 1)  х₁₁ +х₁₂ +…+ х_1j + …+ x_1n = 1,  j = 1(1)n;

(i = 2)  х₂₁ +х₂₂ +…+ х_2j + …+ x_2n = 1,  j = 1(1)n;

(i = 3)  х₃₁ +х₃₂ +…+ х_3j + …+ x_3n = 1,  j = 1(1)n;

   …..     ……     …….            ……            ……      

(i = i)  х_i1 + х_i2 + … + х_ij + … +  x _in = 1,  j = 1(1)n;

….  …    …..     …..     ….      …      …  ….       ….. ….

(i = n)  х_n1 +х_n2 +…+ х_nj + … + x _nn = 1; j = 1(1)n.

Каждая (i-я) строка обозначает возможность прибытия на (j-й) склад любого (j-го) из (n) тягачей и представляется суммой, в которой будет выбран один единственный элемент (x_ij = 1).               Относительно столбцов j = 1(1)n системы уравнений также составляются суммы, и каждая из таких сумм также равна единице. В столбцовых суммах также выбирается единственный элемент(x_ij = 1) Таким образом, будет выбрана таблица (0,1-матрица), заполненная единицами и нулями, но так, что в каждой строке и в каждом столбце оказывается единственная единица. Такие матрицы в математической статистике называются дважды стохастическими. Каждая матрица реализует план Х перевозок и ему соответствует определенное (после подстановки переменных плана в выражение целевой функции) значение ЦФ. Сколько же планов-решений Х можно построить?  Это легко посчитать. Первый тягач можно направить в любой из n складов, но второму тягачу будут доступны только n–1 складов, третьему n–2 складов. Этим трем тягачам соответствует n(n–1)(n–2) количество планов равное произведению трех сомножителей. Далее число возможностей выбора склада будет сокращаться (для 4-го тягача только n–3 выборов), а для последнего n–го тягача останется единственная возможность, так как все остальные склады уже распределены между n–1 тягачами, всего планов будет |Х[i, j]|= n! Например, если n = 20, то

|Х[i, j]| = 20! = 2 432 902 008 176 640 000.

Это 20-ти значное число показывает, что простой перебор хоть и решает все задачи дискретного программирования, но жизни нескольких поколений не хватит, чтобы такой перебор выполнить. Хотя тягачей и складов всего по 20 штук, но самые совершенные компьютеры «повиснут» на подобных вычислениях. Подобная картина в настоящее время имеет место в криптографии. Путем подстановки пробного ключа в дешифратор на выходе можно в случае успеха получить исходный открытый текст. Но ожидать этого, право не стоит. Среди моих публикаций есть одна, где ключ шифра раскрывается за три шага. Но это скорее промах автора примера, который я использовал из пособия для подготовки криптографов, чем везение или мое уменье проводить атаку на шифр. По аналогии с диагональной матрицей (единицы расставлены на главной диагонали) все дважды стохастические матрицы называют диагональными.

В терминах задачи конкретная диагональная матрица Х называется планом-решением. Множество возможных планов классифицируется: планы игнорирующие ограничения называются возможными, планы, учитывающие ограничения (не нарушающие ограничений), называются допустимыми, а подмножество допустимых планов, доставляющее целевой функции экстремум называются оптимальными планами.

Основные понятия и термины ИО

Операция – это организуемое мероприятие (система действий), объединенное единым замыслом, обеспеченное средствами, ресурсами, усилиями и направленное к достижению определенной сформулированной цели.

Цель — это описание желаемого состояния или запланированного результата деятельности, на создание (получение) которого направлены ресурсы, усилия. Чаще всего цель или цели (дерево целей) оформляются в форме требуемых значений различных показателей (в ТТЗ на НИР, ОКР и др.)

Модель — условный образ реального объекта (операции), отражающий его существенные свойства — физический или абстрактный: скульптура, барельеф, игрушки, фотография, карта, схема, рисунок, формула, уравнение, система уравнений, неравенств, граф, сеть, совокупность формул, схем и текста.

Решение – это какой-то конкретный выбор из полного ряда возможностей (ограничения задачи не учитываются).

Допустимые решения — те решения, которые удовлетворяют наложенным в задаче ограничениям.

Оптимальными решениями – являются те допустимые решения, которые по тем или иным соображениям предпочтительнее других и доставляют экстремальные значения ПЭ. Поэтому основной задачей исследования операций является предварительное количественное обоснование оптимальных решений. Предъявление требования к вероятности выполнения задачи одно из главных при организации исследования. Необходимость принятия решения диктуется наличием цели, которую нужно достичь, например, выполнить плановое задание, выбрать тип прибора, построить план перевозок. Если же цель поставлена или фактическое состояние не соответствует желаемому, то имеет место проблемная ситуация, процесс выработки плана устранения которой и составляет сущность задачи принятия решений.Результат операции зависит от способа ее проведения, организации, т.е. от выбора определенных параметров.

Принятие решений обычно выходит за рамки исследования операций и относится к компетенции ответственного лица,  чаще – группы лиц, которым предоставлено право окончательного выбора и на которых возложена ответственность за этот выбор. Делая выбор, они могут учитывать, наряду с рекомендациями, вытекающими из математического расчета, еще ряд соображений (количественного и качественного характера), которые этим расчетом не были учтены.

Эффективность операции — степень ее приспособленности к выполнению задачи, часто измеряется вероятностью выполнения задачи, количественно выражается значением показателя  целевой функции.

Чтобы сравнивать между собой по эффективности разные системы, решения нужно выбрать, т.е. назначить в модели какой-то количественно измеряемый показатель, так называемый

Показатель эффективности (ПЭ) – его часто называют «целевой функцией» задачи. Этот показатель выбирается так, чтобы он отражал целевую направленность операции. «Лучшим» будет считаться то решение, которое в максимальной степени способствует достижению поставленной цели.

Большие промышленные, экономические и военные системы с середины прошлого века стали пристально изучаемым объектом в научных  исследованиях особенно в области управления системами, в военном деле.  Примером объекта в классе больших систем можно назвать такой, в котором объединяются системы организационного управления, решающие задачи руководства производственными и другими процессами и системами.

Критерий эффективности (КЭ) – правило, обеспечивающее фиксирование итогового успешного результата исследования. Рассматриваются три типа КЭ: критерий пригодности системы (система удовлетворяет требованиям, предъявляемым к ней); критерий сравнения систем (из двух или более выбирается та, ПЭ которой предпочтительнее); критерий оптимальности (из всех возможных значений ПЭ выбирается экстремальное при условии допустимости решения). Сам ПЭ не является критерием, так как критерий — это правило, обеспечивающее окончательное принятие решения о пригодности, превосходстве или оптимальности процесса (системы). КЭ не вычисляется, а проверяется.

Характеристика научной дисциплины ИО

Исследование операций (ИО) – область науки, основанная на применении современных разделов математики и тесно связанная с экономикой, кибернетикой, теорией управления системами и другими науками. Целью ИО является получение оптимальных решений задач, возникающих в процессе функционирования или создания сложных систем, включающих коллективы людей, машины и средства вычислительной техники. ИО – это комплекс научных методов, призванных решать задачи организационного управления.

В экономике государств до промышленной революции товарное производство было представлено главным образом мелкими предприятиями, где все руководство осуществлял один человек, сам хозяин. Он делал закупки, планировал и направлял работу, сбывал продукцию, нанимал и увольнял работников. Изменение и рост масштабов производственных систем привел к дифференциации направлений деятельности, произошло разделение труда, а вместе с ним и производственных, и административных функций. Возникли новые разнородные задачи. Важной целью ИО, как дисциплины, возникшей в связи с развитием масштабных промышленных организаций, является обеспечение руководства большими системами научной основой для решения задач, связанных с вопросами взаимодействия различных подразделений систем и организации в интересах общих целей всей организации. Решение, которое представляется наиболее выгодным (предпочтительным) для всей организации в целом, считается оптимальным решением. Эффективность функционирования каждой части в системах зависит от отлаженности механизма в целом, а эффективность работы всего механизма зависит от того, как функционирует каждая часть.  Новые понятия такие как заказчик и исполнитель, показатели и критерии эффективности, функции полезности и  ограничений приобрели значение и вес, новые термины такие как квалиметрические показатели, аудит производственных систем и процессов и др. стали повседневностью.

Применение научных методов к построению технических (механических) систем и систем «человек-машина» часто называют «анализом систем» и ставят знак равенства между ними и ИО. В военной области в определенном смысле конструирование и оценка боевых систем и систем связи является операционным исследованием. Важной и одной из наиболее существенных черт исследования операций является стремление находить оптимальное решение, определять оптимальную стратегию, конструкцию. Задача ИО заключается не в том, чтобы найти решение лучше существующего, а в том, чтобы найти самое лучшее решение из всех возможных. Такое решение на всегда удается получить из-за ограничений, накладываемых современным состоянием и развитием науки, недостатком времени, средств или возможностей. Можно сказать, что ИО в самом общем смысле может быть охарактеризовано как применение научных принципов, методов и средств к задачам, связанным с функционированием организационных систем, с целью предоставить тем, кто управляет этими системами, оптимальные решения. 

Предметные процессы ИО и задачи

В зависимости от типов системных процессов методы и средства их реализации можно разнести по нескольким классам. Приводимые ниже примеры процессов и задач дают представление о предметной области теории ИО, но конечно, не исчерпывают их множества и разнообразия.

Процессы обслуживания

Такие процессы порождаются возникновением клиента, требующего обслуживания. Процесс обслуживания при этом характеризуется явлением ожидания. «Ждет» либо клиент, либо система (редкий случай, когда ожидания отсутствуют). Известно, что все виды ожидания связаны с расходами. Задача заключается в том, чтобы регулировать появление клиентов или определять объем и организацию обслуживания с тем, чтобы свести к минимуму оба вида ожидания и связанные с ними расходы.

Для решения описанной задачи с ожиданиями применима теория очередей. Для задачи определения порядка обслуживания клиентов применима теория расписаний. Наконец, к задачам  определения распределения и группировки каналов и других элементов процессов обслуживания в систему обслуживания применима теория балансирования линий.

Процессы распределения

Подобные процессы возникают, когда, во-первых существует ряд операций, которые необходимо выполнить, и ряд различных путей их выполнения, во-вторых, нет в наличии ресурсов или средств, обеспечивающих выполнение каждой из этих операций наиболее эффективным образом.

Задача заключается в соединении операций и ресурсов таким образом, чтобы добиться максимального общего эффекта. При задании одного (из ресурсов или операции) необходимо определить при каком втором в комбинации с заданным первым можно в конечном итоге добиться наибольшего эффекта. Для получения решения применимы теория линейного программирования и другие виды математического программирования.

Процессы управления запасами

Проблемы, связанные с запасами, порождают процессы, требующие либо обоих либо одного из двух решений: во-первых, сколько заказывать (производить или покупать) и во-вторых, когда заказывать. Эти решения требуют регулирования запасов, что связано с затратами по одной или нескольким из следующих статей: заказ или переоборудование; дефицит или задержка; изменение уровня производства или закупок. Для получения решений используются уравнения экономичного размера партии, а также теории линейного,  динамического и квадратичного программирования.

Процессы замены

Существуют два основных класса, связанных с видами износа оборудования: во-первых, оно устаревает и становится несовременным (менее эффективным) в результате длительного срока службы, или появления нового оборудования (например, станки), во-вторых, не устаревает, но полностью выходит из строя, «гибнет» (например, электролампы). Замена шифрключей, алгоритма шифрования требует определения временного интервала несменяемости шифрключа.

Для устаревающих видов оборудования задача заключается в установлении времени замены с тем, чтобы сократить расходы на новое оборудование, на ремонт и эксплуатацию старого или расходы, связанные со снижением производительности оборудования. Задача относительно оборудования полностью вышедшего из строя ­– определить какие элементы следует заменить и как часто их менять с тем, чтобы снизить расходы на оборудование, на замену частей и другие затраты, связанные с выходом из строя.

Состязательные процессы

Процессы, в которых участвуют две или более стороны, как правило, с противоположными интересами называют состязательными. Эффективность решения одной стороны может оказаться сниженной в связи с решением другой стороны. Ситуацию с таким процессом часто называют игрой.

Игры характеризуются количеством участников, правилами игры, сформулированными с учетом всех возможных допустимых действий, некоторым множеством конечных состояний (выигрыш, проигрыш, ничья и т. п.) и наградами или потерями, вызываемыми этими результатами. Решение задач в состязательных процессах обеспечивается теорией игр.

Похожий, но не совпадающий с игрой процесс называется аукционный торг, отличается признаками: количество участников обычно неизвестно, количество партий, как правило, не ограничено, награды и проигрыш заранее неизвестны и могут быть лишь примерно оценены, результат состязания (выигрыш, проигрыш) также неизвестен и может быть только оценен. Теории торгов еще нет, но некоторые полезные средства для решения и этих задач уже имеются.

Этапы операционного исследования

Как можно представить процесс, порядок операционного исследования? Принято в такое исследование включать следующие пункты.

1. Постановка задачи.

2. Построение математической модели изучаемой системы

3. Нахождение решения с помощью модели.

4. Проверка модели и получение с ее помощью решения.

5. Построение процедуры подстройки решения.

6. Осуществление решения.

Постановка задачи (рис.1). Задача должна быть сформулирована с позиции заказчика и исполнителя операционного проекта. Применяется системный подход, тесно связанный с установлением целей. Заказчик – это лицо (или группа лиц), которое руководит исследуемыми операциями, т.е. тот кто принимает решение. Предварительно необходимо провести анализ системы, находящейся под управлением заказчика, а также его целей и возможных вариантов действий. Задача исследования заключается в том, чтобы определить какой из возможных вариантов действий наиболее эффективен в отношении множества связанных с проблемой целей. Таким образом, при постановке задачи должен быть установлен некоторый критерий эффективности и определена его пригодность.

Построение математической модели (рис.1). Модель выражает эффективность исследуемой системы как функцию множества переменных, из которых по крайней мере одно поддается управлению. Операционная модель в общем виде может быть представлена соотношением

где Е – показатель эффективности системы; х,у – неуправляемые переменные, u_i – управляемые переменные, F(x,y, u_i) — целевая функция модели. Ограничения, накладываемые на переменные модели, выражаются системами равенств или неравенств дополнительно к основному соотношению – показателю эффективности модели, Аrgextr F(x,y, u_i) – критерий эффективности примененный к целевой функции. Следует заметить, что в публикациях авторы критерием эффективности называют показатель эффективности, а критерий вообще опускается из рассмотрения. КЭ, трактуемый как правило (руководство), не измеряется числом. К этим вопросам следует отнести и вопрос о существовании разных шкал для проведения измерений с учетом отношения, отвечающего той или иной шкале.

Вычисления в рамках модели могут выполняться аналитическими или численными методами. Первые выполняются подстановкой значений переменных в формулы, полученные на основе выводов в рамках модели или на основе теорем теории. Численный метод состоит в подборе различных значений для управляемых переменных модели, сопоставлении полученных результатов и выборе того набора значений, который дает наиболее выгодное решение. Численный путь может охватывать широкий диапазон от простого метода проб и ошибок до сложных итераций, которыми пользуются, чтобы подойти к оптимальному решению. При имитационном моделировании для расчетов применяется метод Монте-Карло.

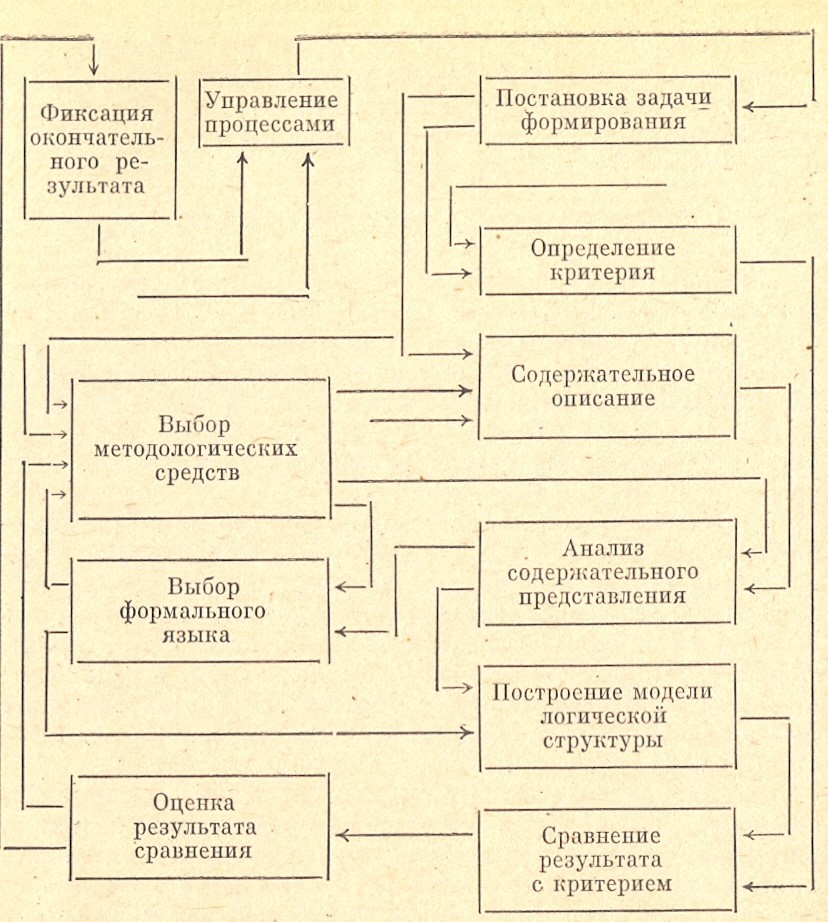
Проверка модели и решения (рис.1). Модель всегда условна и лишь частично отображает действительность. Адекватность модели может быть проверена путем определения степени точности предсказания влияния тех или иных изменений. Хорошей считается та модель, которая несмотря на свою неполноту, может достаточно точно предсказывать влияние изменений в системе на общую эффективность всей системы. Модельное решение может быть оценено путем сопоставления результатов, полученных без использования данного решения, и результатов, полученных при его применении. Оценки могут проводиться ретроспективно с использованием ранее полученных данных или путем практических испытаний и предварительных проверок. Именно проверка при тщательном анализе данных обеспечивает правильный вывод о том, какие данные являются существенными для системы и ее эффективного функционирования, а какие нет.

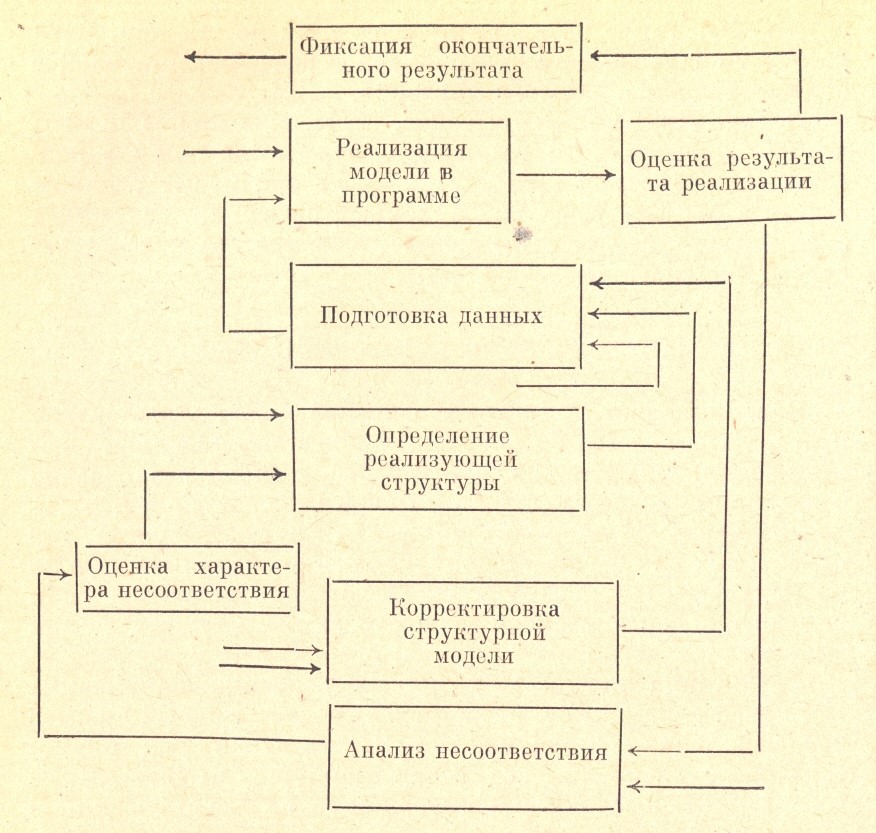
Построение процедуры подстройки решения (рис.2). При изменении одной или более неуправляемых переменных, либо изменении одного или более отношений между переменными существенно изменилось модельное решение выходит из под контроля и утрачивается возможность управлять этим решением. В этих ситуациях решение необходимо подстраивать. Для этой цели надо разработать средства определения того, когда возникают существенные изменения: также должны быть установлены правила такой модификации решения, которая учитывала бы изменения.

Осуществление решения (рис.2). Проверенное во всех отношениях решение представляется для последующего применения в виде ряда рабочих процедур, которые могут быть легко поняты и применены теми, кому поручено их осуществлять. Существующие процедуры при этом как  и ресурсы должны быть изменены. Перечень перечисленных этапов практически никогда не реализуется так как предписано. Некоторые этапы выполняются совместно, некоторые в измененной последовательности. Все части системы постоянно взаимодействуют друг с другом, влияют на процессы и часто на саму формулировку задачи, приводя к ее корректировке.

Методы реализации процессов ИО и их логическая структура

Рене Декарт, описывая развитый им метод научного исследования, формулирует четыре основных его правила [3].

1. Разбиение сложной проблемы на более простые последовательно до тех пор, пока не будут найдены далее неразложимые компоненты.

2. Нерешенные проблемы следует сводить к решенным. Этим путем находятся решения простых проблем.

3. От решения простых проблем следует переходить к решению более сложных, пока не будет получено решение проблемы, которая являлась исходной при разбиении и является конечной в данном процессе.

4. После получения решения исходной проблемы необходимо рассмотреть все промежуточные, чтобы удостовериться, не пропущены ли какие-нибудь звенья. В случае, когда полнота решения установлена, то исследование завершается; при обнаружении пробела в решении необходимо дополнительное исследование в соответствии с перечисленными правилами.  Метод рекомендуется применять всегда при разработке операций

Следует сказать несколько слов о логике исследований и методологических понятиях [2}. В методологии науки разработаны общие понятия для описания конкретных методов и проводимых в их рамках процессов научного исследования. Эти описания играют важную роль при выявлении связей между различными методами в составе сложных исследований. Поэтому необходимо использовать эти понятия для методологического описания логики проводимых исследований.

Так проверка и корректировка гипотез производятся с помощью хорошо известных пяти методов индукции, создание и развитие которых связано с именами Ф. Бэкона и Дж. Милля [4, 5].

Причинная связь явлений устанавливается методами единственного сходства (на основе фактов, полученных в наблюдении), единственного различия ( на основе фактов, полученных в эксперименте), объединенным методом (на основе совместно используемых фактов обоих видов). Метод остатков применяется при выявлении неизвестной причины изучаемого явления, а с помощью метода сопутствующих изменений анализируется динамика причинных зависимостей [6, 7 , 9].

Постановка задачи

Начало любого исследования – постановка задачи, более того, существует мнение, что половину успеха в деле составляет удачная или правильная постановка задачи. В действительности все не совсем так. Часто не сформулировав задачу в завершенном виде, переходят к следующей стадии – формированию модели системы и процессов, протекающих в ней. К постановке задачи возвращаются многократно, корректируют ее элементы и собственно формулировку, т.е. по ходу процесса исследования задача непрерывно меняется и уточняется. Это продолжается вплоть до получения решения задачи. Иногда до момента завершения исследований неизвестно, правильно ли была поставлена задача, и тогда вопрос так и остается открытым.

При проведении исследований обычно стремятся скорее включиться в работу, но не надо торопиться следует руководствоваться некоторыми стандартными процедурами постановки задачи и выделять для этого определенное время. Здесь рассмотрим идеализированный процесс постановки задачи, который является наилучшим из существующих, при условии, что нет никаких ограничений. На самом деле на практике редко встречаются такие идеализированные условия.

Дело в том, что ИО предполагает исследование экономики операций, не исключая при этом своих собственных операций. Неправильные представления об экономической стороне дела создают представления о различиях между реальным процессом и идеализированным. Эти различия не являются «чисто белым иили черным», а определяются чаще всего экономическими соображениями.

«Практики» стремятся удешевить схему (в рамках проведения тендера, антимонопольное ведомство не спит), что удается сделать относительно близких тактических целей, но теряется ощущение стратегического восприятия, что в итоге обходится дороже. Идеальный подход, наоборот, во главу угла ставит стратегические вопросы, минимизируя затраты времени и средств, но в тактических вопросах сопряжен с большими расходами. Правильное экономическое решение – удачный компромисс между затратами, связанными с достижением тактических и стратегических целей. Важны точное знание идеального решения необходимость и понимание того к чему следует стремиться. Недооценивание возможностей идеального решения может дорого обойтись впоследствии.

Элементы задачи ИО

Рассмотрим в деталях элементы задачи. Очевидно, что перед руководителем или группой лиц должна стоять задача. Эти люди не удовлетворены положением дел в какой-то предметной области и стремятся найти решение, чтобы изменить ситуацию в лучшую сторону. Назовем такую группу или отдельного руководителя лицом, принимающим решение (ЛПР). Таким образом, первым элементом задачи является лицо, принимающее решение (часто это заказчик).

Во-вторых, для существования задачи необходимо, чтобы человек, принимающий решение, желал изменить положение, т.е. должны быть понятными некоторые цели, которых надо достичь. Цели, по существу – это требования к выходному эффекту системы. Цели – второй элемент задачи.

В–третьих, задача связана с какими-то условиями или средой, в которой учитывается наличие или отсутствие различных ресурсов. Такой средой в задачах исследования операций обычно является организационная система, включающая людей и машины. Система или среда является третьим элементом задачи.

В-четвертых, необходима (должна существовать) возможность выбора между различными (по крайней мере двумя) способами действия или политиками. При отсутствии выбора задача не возникает. Задача всегда включает вопрос: что делать? Но сам этот вопрос становится задачей только в том случае, если существуют различные пути достижения цели. Различные способы действия (стратегии) являются четвертым элементом задачи.

Чтобы сформулировать исследовательскую задачу, необходимо выполнить следующие операции.

1. Уточнить перечень целей, определенных на первом этапе постановки задачи.

2. Уточнить перечень различных стратегий достижения целей.

3. Определить меру (показатель и критерий) эффективности исследуемой системы.

Взаимодействие исполнения и управления при ИО

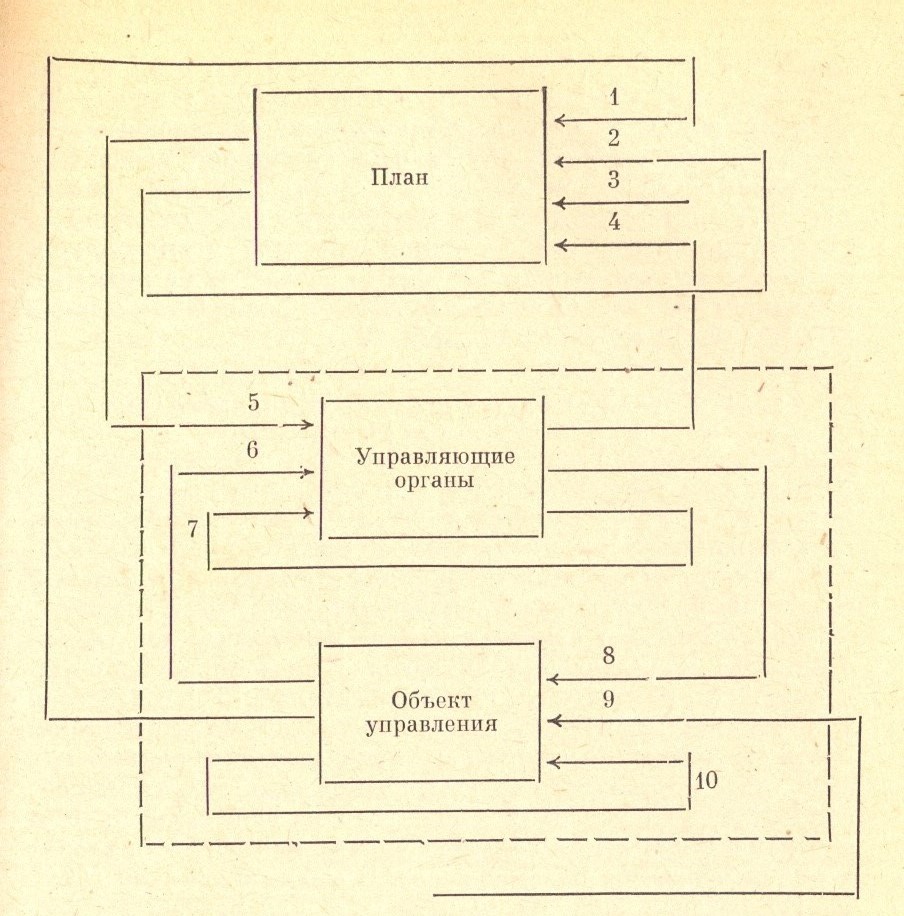
Планирующая система связывает объект управления с управляющими органами. В процессе деятельности объекта (рис. 3) происходит преобразование одного состояния объекта в другое (10), что зависит от изменения внешних обстоятельств (9) и предписаний (8), вырабатываемых органами управления на основании плановых представлений объекта (5) и оценок текущего состояния объекта управления (7). Оценки вырабатываются на основании показателей и критериев эффективности (5) и информации (6) от объекта управления. Вся эта цепочка определяет один такт в преобразовании объекта из одного состояния в другое. Для каждого такта необходима своя часть плана. Поэтому после выполнения одного такта в самом плане управление передается следующей его части, что обозначается стрелкой (2) на рис. 3.

Настройка плана на объект осуществляется с помощью информации (стрелки 1 и 4) об объекте управления и плановых органах. Все текстовые предложения, входящие в планы, подразделяются на два вида – дескриптивные (описывающие) и прескриптивные (предписывающие). С помощью первых представляются состояния, отражаемых в плане объектов, а вторые — служат для выражения предписаний по использованию того или иного способа перехода из одного состояния в другое. Посредством выделения предложений рассматриваемых видов определяются семантические свойства планов.

Такая настройка состоит в выборе дескриптивных и прескриптивных частей плана, которые отвечают требованиям текущего момента. Именно здесь могут выбираться способы перехода, варианты, категории и т. д. В этой настройке определенную роль играет получение информации от окружающей среды (3).                                                                                                                                       

Итак, логическая структура планов, их синтаксические и семантические характеристики непосредственно связаны с обобщенным анализом поведения соответствующих объектов. Оно представляется как чередование двух операций – тактов преобразований состояний объектов управления и настройки планов на их объекте. На практике это позволяет проводить логический анализ процессов реализации планов как процессов применения знаний.

Литература

1. Азгальдов Г. С., Райхман Э. П. О квалиметрии.– М.: Изд. Стандартов, 1973.–172 с.

2. Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.

3.  Декарт Р. Рассуждения о методе с приложениями (Диоптрика, Метеоры, Геометрия) –М.: Изд-во АН СССР, 1953.–с.9-66.

4. Бэкон Ф. Новый органон.– М.: Соцэкгиз,1938. –244 с.

5. Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.

6.  Джини К. Логика в статистике.– М.: Статистика,1973. –127 с.

7.  Квейд Э. Анализ сложных систем. – М.: Советское радио,1969.–519 с.

8.  Квейд Э. Методы системного анализа // Новое в теории и практике управления производством в США.–М.: Прогресс, 1971.– с.78-99.

9.  Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.

10. Клыков Ю. И. Ситуационное управление большими системами. – М.: Энергия,1974.–135 с.

11.  Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.

12.  Пфанцагль  И. Теория измерений. – М.: Наука, 1988.–384 с.

13. Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.

14. Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.