Эту вещь я хотел сделать с детства, но тяжело такое имплементировать, когда у тебя что на ЕС-1022, что на СМ-4 не хватает памяти. Сейчас такие вещи делаются играючи.
Итак, засеем бесконечное поле в игре «Жизнь» клеточками с вероятностью p от 0 до 1. Какова будет плотность популяции клеток после N ходов?
Технические детали: я стащил код отсюда и менял его под себя. «Бесконечное» поле замкнуто на тор, чтобы уменьшить краевые эффекты. Размер поля обычно брался 1000×1000. И да, python это плохой выбор для таких вычислений — вот тут я вижу как достигают скорости 2.5 миллиона evaluated cells per second на CPU и 25 миллионов — на GPU.
Первые два хода
Первый ход можно вычислить аналитически. Вероятность того, что вокруг клетки находятся n (от 0 до 8) заполненных клеток при вероятности p составляет:
Вероятность рождения новой жизни в пустой клетке, если вокруг ровно три соседа:
а смерти
Новая плотность
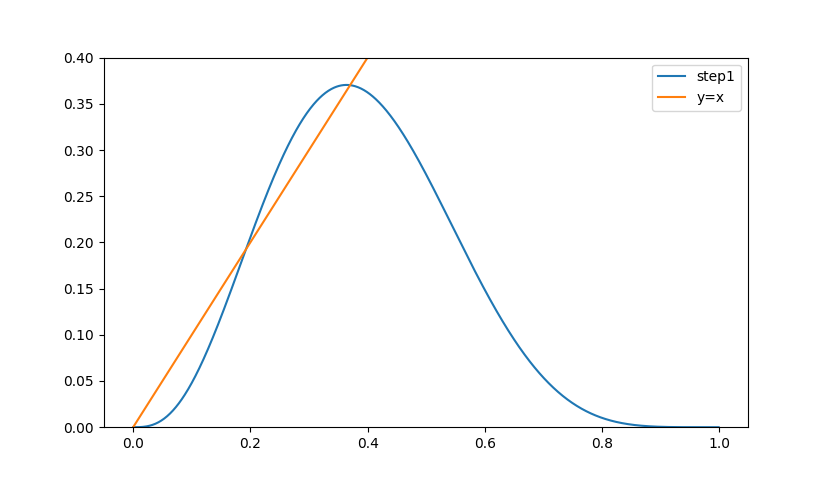
Интересно, что кривая имеет две фиксированные точки (x=y), и на небольшом промежутке начальная плотность даже увеличивается, достигая максимума в 0.37. Численный эксперимент согласуется с этим результатом:
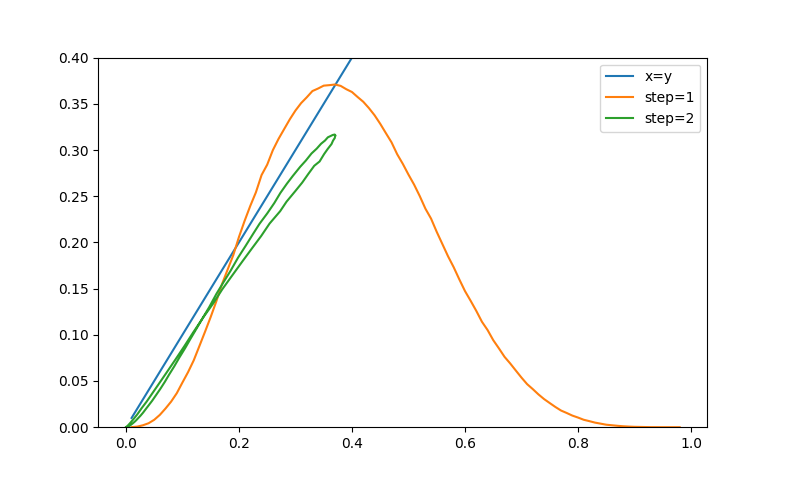
После первого шага мы вновь получаем хаос, хаос другой плотности (p1). Этот хаос отличается от первичного хаоса, и правила первого шага ко второму не применимы. Конечно, для второго шага мы тоже могли бы написать аналитическое выражение, но оно такое огромное, что это практически нереально.
Интересно построить график, где на x находится p1 (плотность после первого шага), а на y — p2 (плотность после двух шагов). Этот график показан зеленым. Как видно, он отличается от оранжевого, и он описывает петлю. Дело в том, что на p1 одна и та же плотность может быть достигнута как при низкой начальной плотности, так и при очень высокой. Петля показывает, что эти два случая тоже немного отличаются по своей эволюции.
Первый десяток и первая сотня
На оси x теперь всегда будем откладывать изначальную плотность, и посмотрим, что происходит в течение десяти шагов:
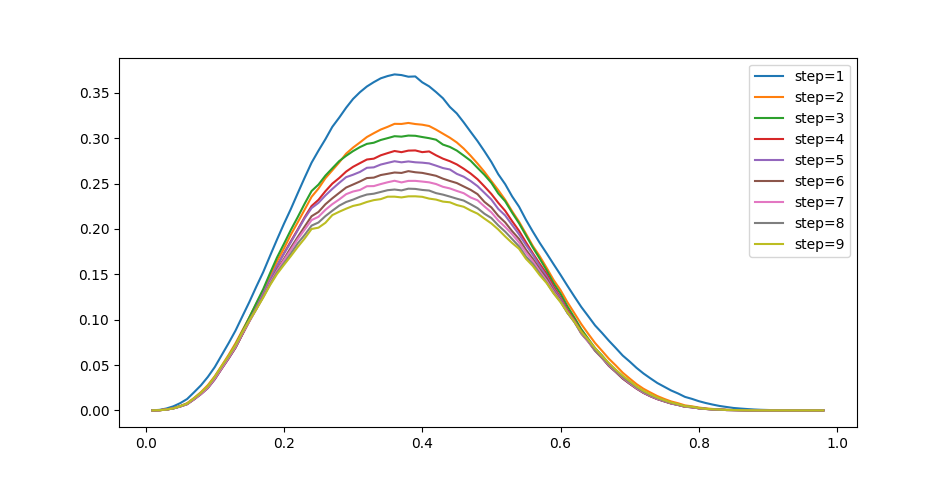
Плотность плавно уменьшается, а максимум сдвигается вправо. Если построить зависимость от времени, то мы увидим интересную вещь:
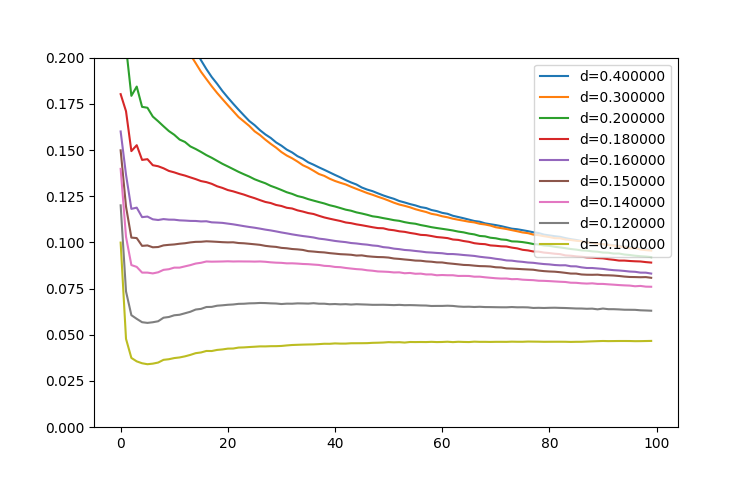
При p<0.15 после первичного и быстрого падения плотности возникает 'ренессанс‘, плотность после нескольких шагов растет некоторое время. К шагу 100 графики для разных плотностей начинают сближаться. Рассмотрим этот эффект подробнее ниже.
Тысячи шагов
По мере эволюции на графике плотности возникает ‘плато’:
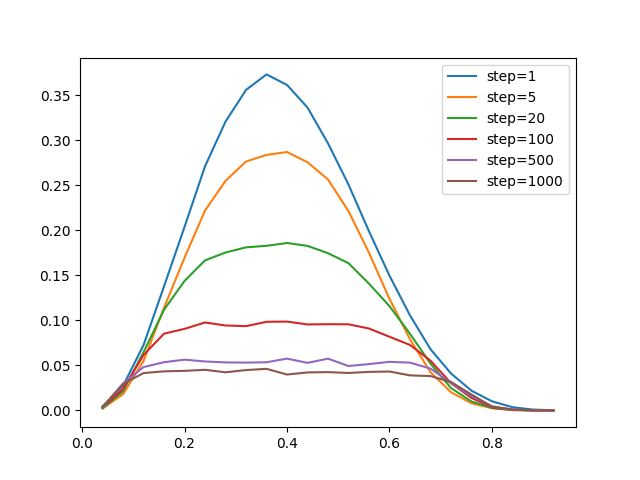
Обратите внимание, что итоговая плотность после тысячи шагов практически не зависит от изначальной в широком диапазоне p от 0.1 до 0.7. Диаграмма по времени:

Эти линии даже пересекают друг друга. Понаблюдав за игрой глазами, я увидел, что на поле есть куча мертвых статических фигур (‘пепел‘), типа блоков из четырех клеток и ‘ульев‘, и ‘движуха‘, где всегда что-то происходит, взрывается, контактирует, касается статических конфигураций и оживляет их. Изначальное значение p здесь роли уже не играет.
Однако постепенно ‘движуха‘ ослабевает. Вначале я думал, что это эффект масштаба. Я провел несколько экспериментов с полем разного размера (300, 500, 1000) и зависимости не заметил.
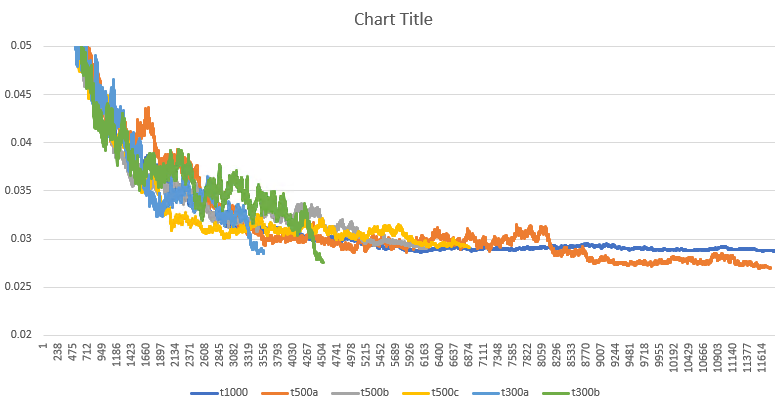
В итоге все заканчивалось ‘пеплом’ плотности около 0.028 — блоки, мигалки, улья и ряд других статических фигур.
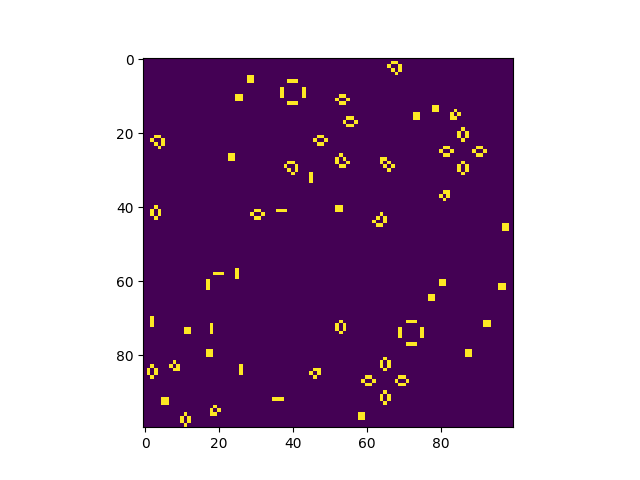
Гугол шагов
Рассмотрим эволюцию при низкой плотности, допустим, p=0.001 Кажется, ничего интересного? Но ведь есть, например, Gosper Glider Gun — ружье, стреляющее глайдерами каждые 14 ходов. Неизвестно, является ли ружье ‘садом эдема‘, но в любом случае оно может получиться чисто случайно. При низкой плотности вероятность появления фигуры из n клеток примерно равна p**n. В ружье 36 клеток, значит вероятность его возникновения в определенном месте равна 1E-102.
Случайно возникшие ружья будут разделены примерно 1 делить на корень из предыдущего числа — 1E51 клеткой. Они будут производить глайдер (5) клеток каждые 14 ходов, то есть 5/14 клетки за ход, постепенно увеличивая плотность, пока сами не будут сжигать друг друга.
Глайдер имеет эффективное сечение 6 клеток, в ружье — ширину 36, то есть зацепить ружье глайдер может на полосе 36+6=6 = 48 клеток. То есть одно ружье убьет другое если попадет в полосу поражения, а на этой полосе одно ружье отстоит от другого на 1E102/48 клеток. Глайдер проходит 1 клетку за 4 хода, то есть он это расстояние пройдет за 1E102/12 шагов. За это время ружье произведет 1E102/12 * 5/14 = 5/168*1E102 клеток, и это в каждом квадрате с ребром 1E51 клетки, то есть в среднем 5/168 = 0.0297 !!! Очень близко к плотности ‘пепла‘! Совпадение?
Это число на самом деле не зависит от начального p — плотность сокращается, будучи и в числителе, и в знаменателе. Я работал с числами, чтобы показать порядки величин. То есть, через гугол шагов ружья организуют ‘движуху’, накачав вселенную глайдерами, Если из до этого не сожгут ‘реликтовые’ глайдеры, получившиеся случайно, и (так как глайдер состоит из всего пяти клеток) в числе куда большем, чем ружья. Зато ружья не двигаются, а реликтовый глайдер наверняка наткнется на фигуру из 4 или 3 клеток, которых еще больше. Итак,
Гипотезы
Первая гипотеза касается окончания ‘движухи’ — в широком диапазоне изначальных плотностей p от 0.1 до 0.7, после окончания ‘движухи’ ‘пепел’ имеет одну и ту же плотность, около 0.27
Так как ружья накачают ‘вселенную’ глайдерами при сколь угодно малой изначальной плотности, и снова начнется ‘движуха’, то вторая гипотеза сильнее:
В пределе при любой плотности p (кроме вырожденных случаев p=0, p=1) получается ‘пепел’ плотности 0.27


