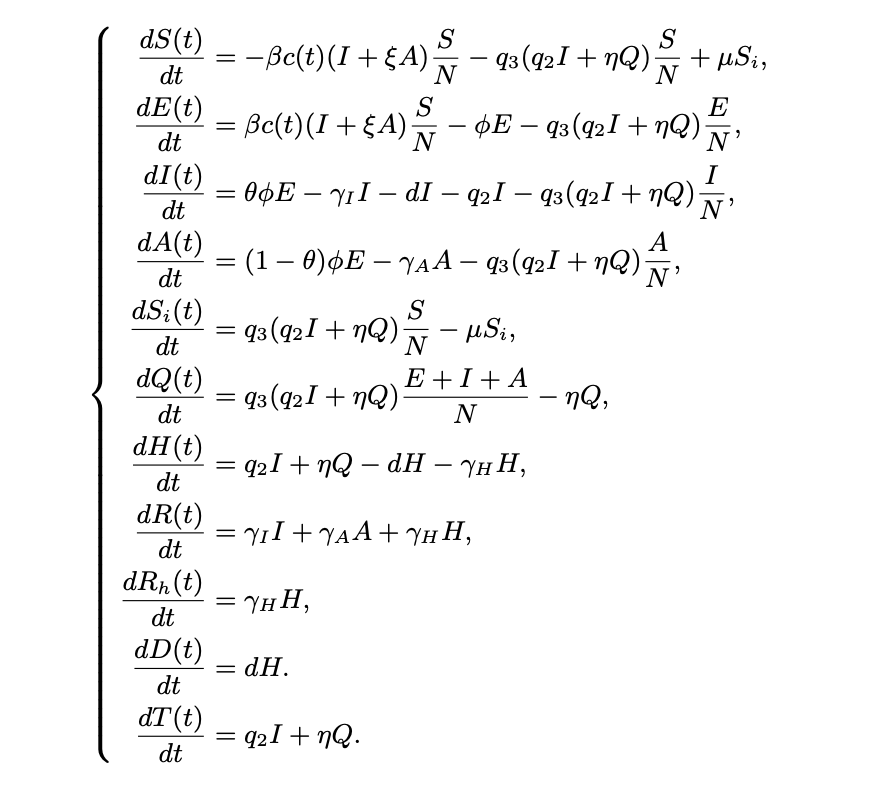Действительно, за последние месяцы тема анализа эпидемии covid-19 уже порядком достала, звуча из всех утюгов, кофеварок и лыж. Да и сама тема уже практически (очень зря) потеряла свою актуальность.
Однако, как раз сейчас, у нас накопился достаточный объем данных по которому мы можем посмотреть как именно развивалась эпидемия и проверить модели, которые использовались ‘в бою’.
Введение
В этой статье мы не будем концентрироваться на жутком матане и тервере, рассматривать экономические или политические последствия и не будем пытаться изобрести свою статистику.
Вместо этого мы:
- Рассмотрим некоторые моменты, подходы и идеи в обработке данных, которые пригодятся при построении модели.
- Построим объемную модель эпидемии.
- И оценим как изменение некоторых параметров может влиять на ход эпидемии.
Disclaimer 1:
В этой статье будет довольно сильный уклон в сторону анализа ситуации по России в целом, и Нижнего Новгорода в частности.Disclaimer 2:
Все модели исходят из официальных данных указанных стран и регионов.Disclaimer 3:
Говоря о России и её регионах, мы сознательно будем убирать последние данные (начиная, примерно, с 15 мая) из-за целого ряда причин. Кратко опишем это как: Изменение методики подсчета заболевших. Однако, это тема для отдельной статьи и мы не будем вдаваться в эти дискуссии сегодня.
Данные
Ну, начнем от печки. Данные по миру, странам с достаточным объемом статистики и их регионам можно найти тут CSSEGISandData, а по России и российским регионам тут стопкоронавирус.рф. Автоматически выгружаем данные из этих источников и формируем удобный датасет.
Для начала, стоит сделать сноску про то, что мы не может оценивать все страны одним и тем же методом. Так как методы сбора статистик, учет заболевших, учет смертности людей с сопутствующими заболеваниями (см. Ломбардийские дедушки) отличаются от страны к стране. (Не говоря уже о различных вводимых властями мерах по предотвращению эпидемии и национальных особенностях, про это немного позже).
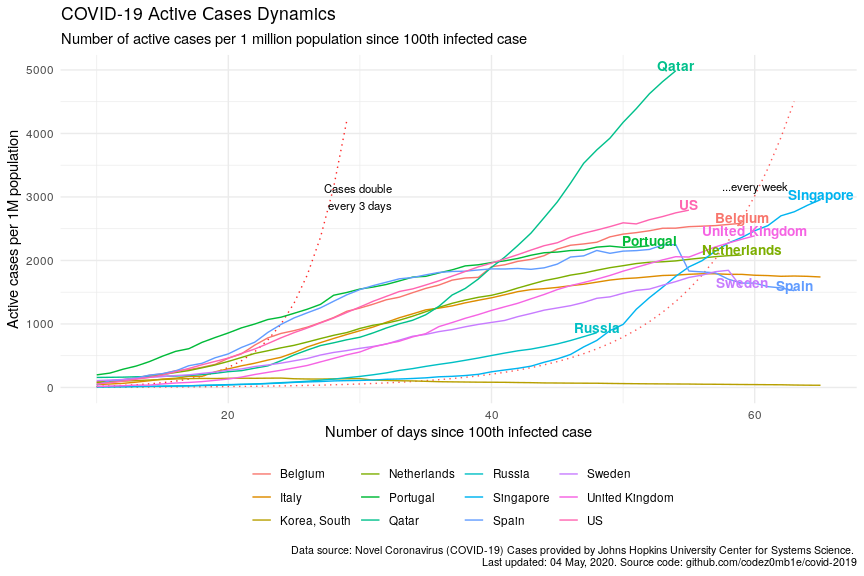
Поэтому сложно предсказывать дальнейшее развитие эпидемии в конкретной стране, опираясь только на страны со схожей динамикой распространения вируса. (Как минимум, из-за существенного отличия тренда Российской статистики и статистики других стран в пересчете на единицу населения.)
source
Еще одна проблема, на которой стоит заострить внимание, — методология сбора и обработки статистики по смертности. Учитываются ли люди, умершие от сопутствующих заболеваний, в то время как они были заражены COVID-19? Учитываются ли умершие с аналогичной симптоматикой, но без проведенного тестирования? Тем более что в России подход к учету статистики драматически менялся без пересмотра уже опубликованных данных.
Можно посмотреть отчет ВОЗ, где рассказывается про различие смерти с коронавирусом и смерти от коронавируса: «crude mortality ratio» и «infection mortality rate». (Для более подробной сводки по смертности можно посмотреть две статьи на habr: раз & два ).
Также, стоит брать во внимание намеренную или случайную неточность данных. И простой факт: чем больше хороших тестов проводится (с малой ошибкой первого рода), тем больше в стране будет выявленно заболевших.
Еще одно интересное наблюдение, которое можно выделить из данных, — это ‘синдром выходного дня’ (как бы странно это не звучало). Значительный спад в количестве подтвержденных случаев наблюдается в понедельник-вторник (понедельники отмечены на графиках), что выполняется для большинства стран.
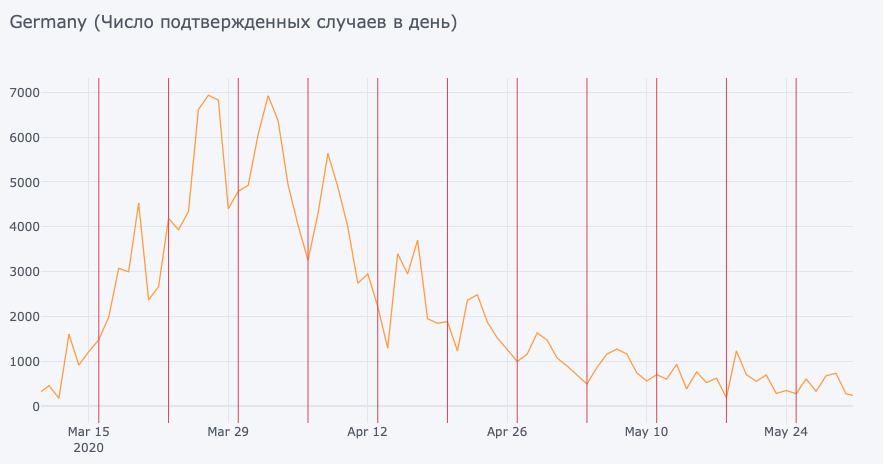
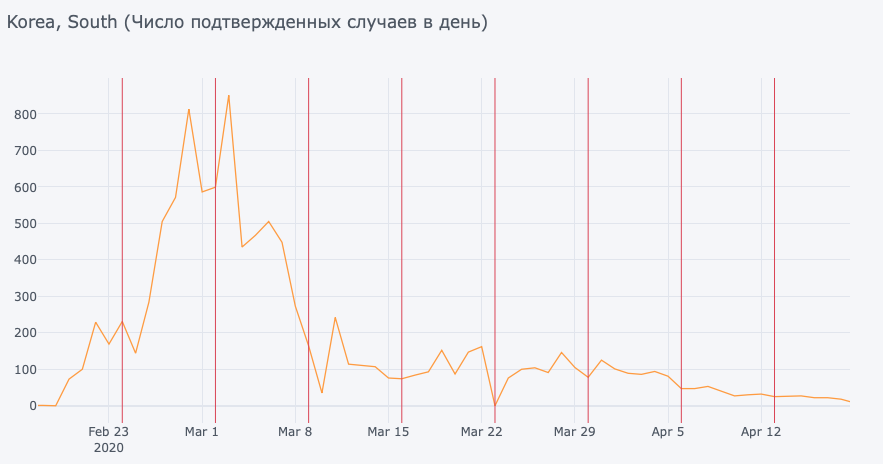
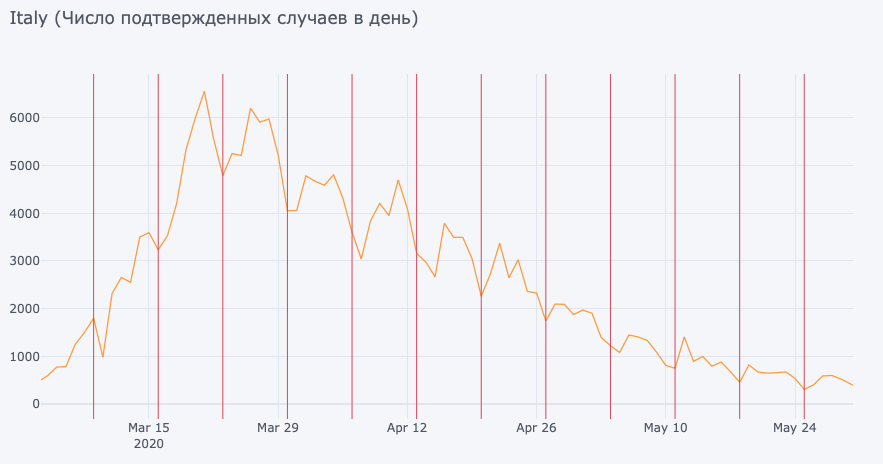
Это, скорее всего, объясняется тем, что в выходные не проводятся (или существенно снижается объем) акции массового тестирования, не работают лаборатории и вызов врача на дом. Поэтому к понедельнику оказывается недостаточно материала для подтверждения новых случаев заражения.
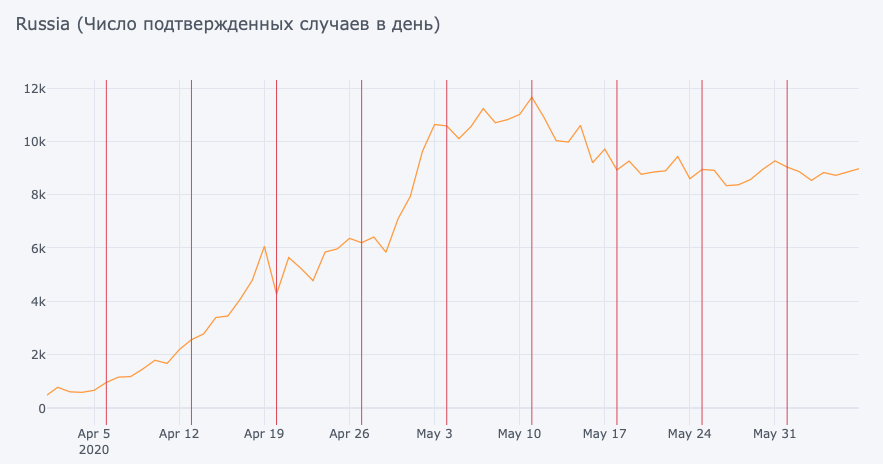
С Россией все несколько сложнее. В целом, если постараться, можно разглядеть этот ‘синдром’ вплоть до, примерно, 11 Мая. (См. Disclaimer 3).
Ну и последний важный момент, связанный с данными. Можно заметить, что в официальной статистике любой страны наблюдается ситуация, когда число заболевших первые несколько недель растет очень медленно или совсем не растет. Как будто мы действительно строим экспоненту и нецелое количество людей округляем вверх.
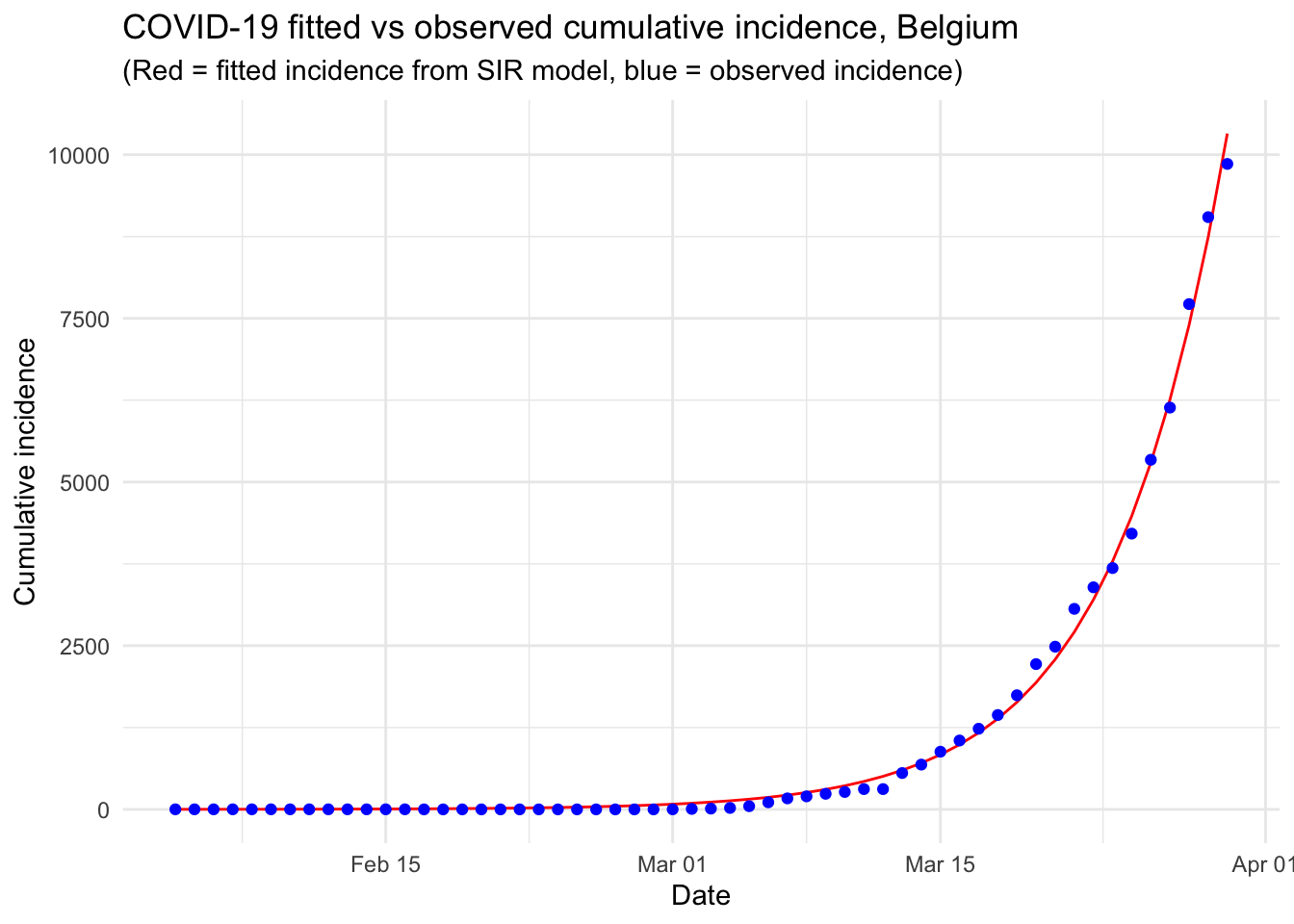
Это легко объясняется продолжительным временем развития первых симптомов у зараженных, отсутствием тестирования в первые дни и простым общечеловеческим раздолбайством. Этот факт понятен визуально, однако, почти любая модель будет довольно сильно «сбиваться» от такого долгого периода застоя. Поэтому далее все данные проходят предобработку и эпидемия будет рассматриваться с момента наличия 300 заболевших для страны и 50 для регионов (если не указано обратное).
Краткий вывод можно сформулировать так: данные разнятся от страны к стране и будет довольно сложно выделить и применять один универсальный метод к любым странам. Как мы увидим позже, страны с ‘очевидно адекватной’ статистикой (доверие к статистике, правильно введенные меры, снятие ограничений после эпидемии, а не во время и так далее) лучше всего будут подходить к модели.
Долгосрочная модель
Вот мы наконец-то и подобрались к основному разделу этой статьи и к самой точной модели, которая, забегая немного вперед, дает довольно адекватные предсказания.
Важным моментом в построении модели является возможность интерпретировать параметры модели и сравнивать адекватность полученных значений параметра с общемировыми (если во всех странах заразность составила около 20%, а в одной конкретной стране почему-то 3%, то что-то тут не то).
Да, можно использовать модель SIR/SEIR, которая уже стала ‘классической’ за последние месяцы. Однако, эта модель слабо интерпретируемая и зависит от предпринимаемых государством мер, уровнем соблюдения изоляции, вероятностью передачи от асимптотических и количеством бессимптомных, да и просто необнаруженных, больных. Все эти параметры можно вбить в модель SEIR железным костылем, но обучение такой модели существенно затруднено. (Пример анализа вариантов развития эпидемии от мер на основе имитационного моделирования такой модели можно посмотреть в красивых видео в нашей прошлой статье)
В основу этой статьи легла публикация китайских ученых «Risk estimation and prediction by modeling the transmission of the novel coronavirus (COVID-19) in mainland China excluding Hubei province», которая была переработана и адаптированна под российские реалии.
В этой статье предложена усовершенствованная модель SEIAR, обобщенная и расширенная дополнительными переменными (о них немного позже). Модель обучалась на статистических данных о заражении в материковом Китае, не включая провинцию Хубэй. (Её исключили на основании того, что здравоохранение было критически не готово к эпидемии, в отличии от остальной части страны, куда вирус дошел позже. Однако, модель с некоторыми оговорками можно экстраполировать и на весь Китай.). Сами дифференциальные уравнения решались с использованием цепей Маркова, а если быть точным, то использовать Markov chain Monte Carlo.
Сама модель хороша тем, что учитываем момент не намеренного занижения статистики — когда просто физически невозможно учесть всех заболевших в симптомных и бессимптомных формах.
Замечание: Важно понимать, что не все значения параметров и выводы можно взять из статьи и принять за абсолютную правду. Разность подходов, развитость экономики, введенные меры и занижение статистики играют существенную роль.
Если кратко, то модель может быть представлена так:
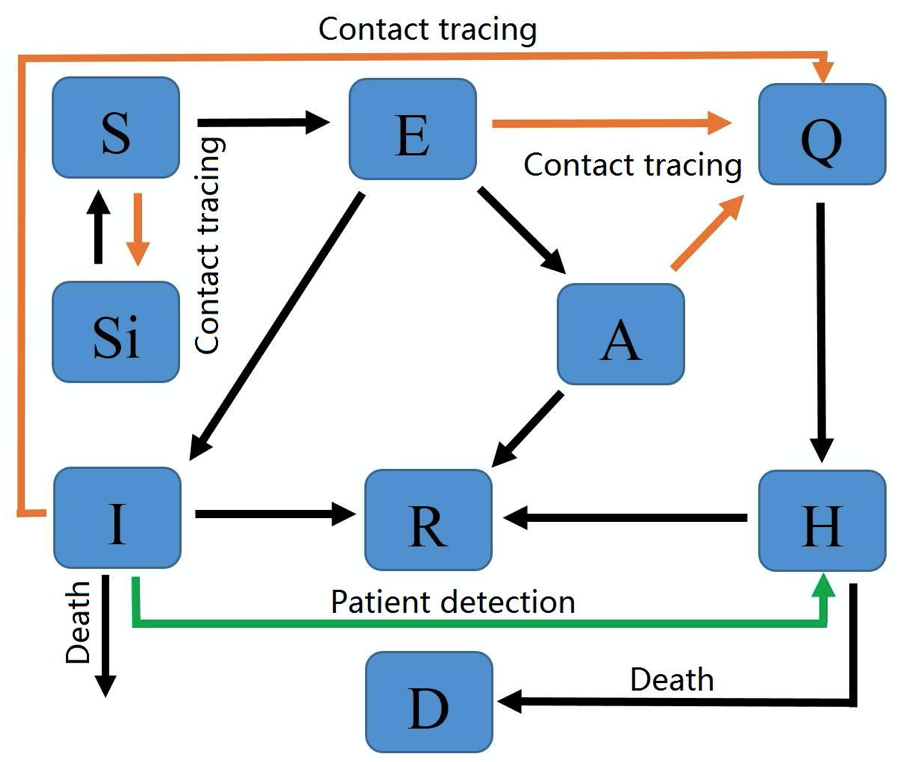
Давайте забежим немного вперед и уже наконец покажем вам картиночку с прогнозом.
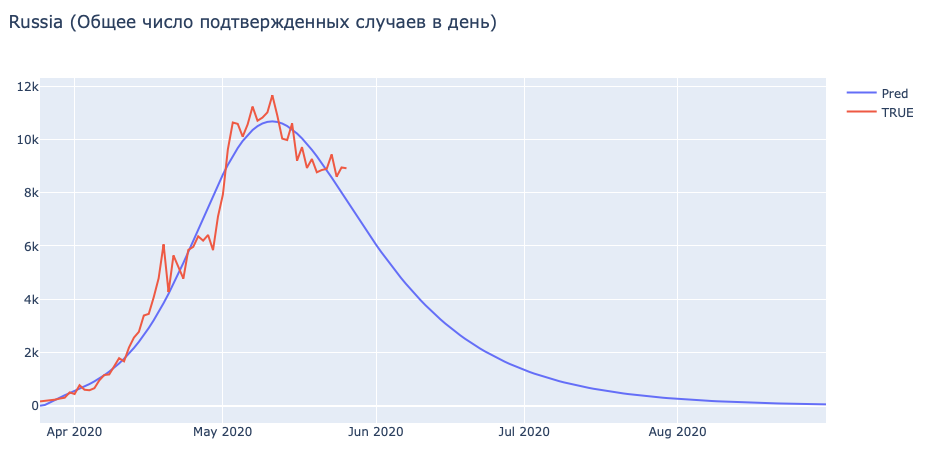
Причем предсказание выглядит вполне адекватно, если а) считать статистику идеально правдивой и б) опираться на опыт других стран при снятии мер.
Запись от 14 мая: Хорошо видно, что пик эпидемии наблюдается прямо вот сейчас. Сейчас самое время всем выйти гулять! (САРКАЗМ)
Но давайте, все же, не делать пока что поспешных выводов и начнем по порядку.
Формальное описание
Итак, под капотом модели работает набор диффуров:
На самом деле, если внимательно посмотреть на описания параметров и формулы (и потратить часок-другой), то становится понятно, что это довольно простая по своей логике система диффур. Основная проблема возникает именно в решении этой системы по имеющимся данным.
Описание всех параметров модели может быть найдено ниже:
| Обозначение: | Описание: | Используемые границы начальных значений: |
| phi | Показатель скорости развития симптомов у зараженных | от 1/15 — 1/4 (то есть от 4 до 15 дней) |
| mu | Показатель длительности самоизоляции (скорости выхода здоровых людей из самоизоляции) |
от 0 — 1/6 (то есть от 6 дней) |
| с_0 | Среднее число контактов в день на человека, значение на начало периода | от 30 до 45 человек в день |
| beta | Вероятность заболевания после контакта с инфицированным | от 0.05 до 0.6 |
| theta | Вероятность проявления симптомов у зараженного (доля симптомных больных среди всех зараженных) | от 0.35 до 0.8 |
| eta | Показатель госпитализированных из числа находящихся на обсервации (скорости госпитализации) | от 0 до 1 |
| gamma_I | Доля выздоровевших среди симптомных больных | от 0 до 1 |
| gamma_A | Доля выздоровевших среди бессимптомных больных | от 0 до 1 |
| gamma_H | Доля выздоровевших среди госпитализированных больных | от 0 до 1 |
| d | Доля общего числа смертей, вызванных вирусом, из общего числа заболевших за весь период | от 0.001 до 0.15 |
| epsilon | Поправочный коэффициент для вероятности передачи от бессимптомных больных | от 0.6 до 0.9 — |
| q_1 | Коэффициент, определяющий меры по ограничению контактов | |
| q_2 | Меры по выявлению инфицированных (тестирование) | от 0.1 до 0.9 |
| q_3 | Меры по отслеживанию перемещений заболевших | от 0 до 30 |
| sigma | Снижение частоты контактов с кумулятивным ростом случаев заражения (определяет экспоненциальное убывание доли контактов с ростом опубликованных случаев инфекции) | от 0 до 0.001 |
После долгих консультаций с эпидимиологами, умственный усилий и получения своей собственной корочки вирусолога, были поставлены адекватные границы для каждого из параметров. Проблема возникает на этапе сравнения с другими странами, так как каждая страна использует свои подходы и возможные границы параметров будут различаться. Поэтому использованы наиболее широкие границы, позволяющие получить хороший результат.
А аппроксимировать и предсказывать мы будем следующие величины:
| Обозначение: | Описание: | Используемые границы начальных значений: |
| S(t) | Уязвимые | |
| E(t) | Зараженные в стадии инкубационного периода | [0, 1e+4] |
| I(t) | Симптомные больные | [0, 1e+4] |
| A(t) | Бессимптомные больные | [0, 1e+4] |
| Si(t) | Изолированные уязвимые | [0, 1e+4] |
| Q(t) | Зараженные на карантине | |
| H(t) | Госпитализированные зараженные | |
| R(t) | Выздоровевшие | |
| Rh(t) | Выздоровевшие из госпиталя | |
| D(t) | Кумулятивное число смертей в госпитале | |
| T(t) | Общее число подтвержденных случаев |
В изначальной статье авторы предлогают использовать метод Марковских цепей Монте-Карло (MCMC). Но этот метод решает предложенные дифуры непозволительно долго и нестабильно. Поэтому мы используем другой метод. Всю эту сложную систему будем решать вполне классическими методами BDF — мы пошагово аппроксимируем производную функции. Метод, конечно, не идеален и имеет много как плюсов как и минусов. Да, можно было решить и очень сложно и красиво, но, совсем не факт, что это дало бы какие-либо значимые результаты.
Также, сама модель была немного отредактирована. Начальные значения зараженных, изолированных, симптомных и бессимптомных больных (от которых начинается решение уравнений) теперь представляют собой параметры, которые мы находим. Также был введен коэффициент снятия ограничений, с увеличением количества контактов в определенные моменты для моделирования второй волны (В статье упор на это делать не будем).
Эксперименты
Проведем моделирование для России. (Еще раз сошлемся на дисклеймер вначале, что мы НЕ рассматриваем статистику начиная с последнего времени из-за полного изменения методики учета)
Если мы считаем, что пик прошел в середине мая ровно в момент обращения президента и конца нерабочих дней.
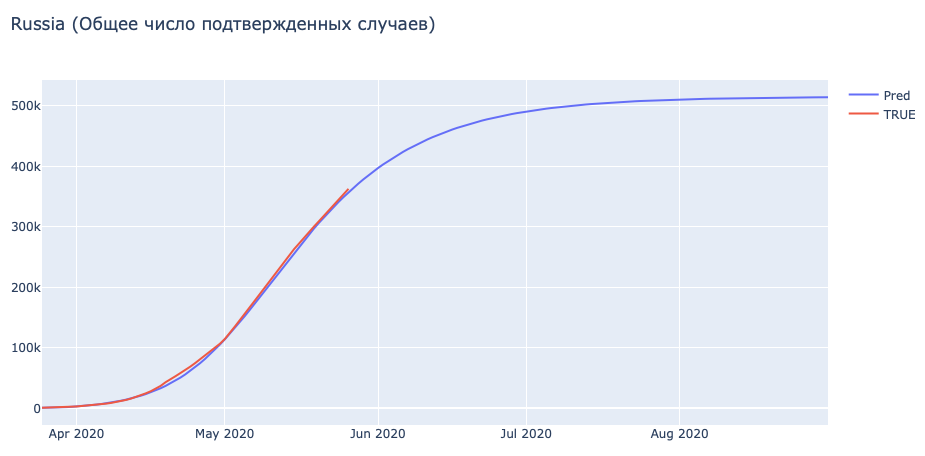

| phi | mu | c_0 | beta | theta | eta | gamma_I | gamma_A | gamma_H | d | epsilon | q_2 | q_3 | sigma | |
| Russia | 0,064 | 0,004 | 30,889 | 0,064 | 0,410 | 0,182 | 0,793 | 0,208 | 0,020 | 0,001 | 0,642 | 0,900 | 12,387 | 0,000007 |
Как будет видно позже, экстремальные значения величины q_3 не будут сильно влиять на результат, а вот величина q_2, которая принимает тут максимально возможное значение при ограничениях показывает нам, что мы не нашли глобальный оптимум, а лишь уперлись в локальный минимум. Его найти будет очень сложно из-за совершенно неоднородной статистики в целом.
Важно учесть, что тут мы именно берем официальную статистику за ground truth и строим предсказания исходя из этого.
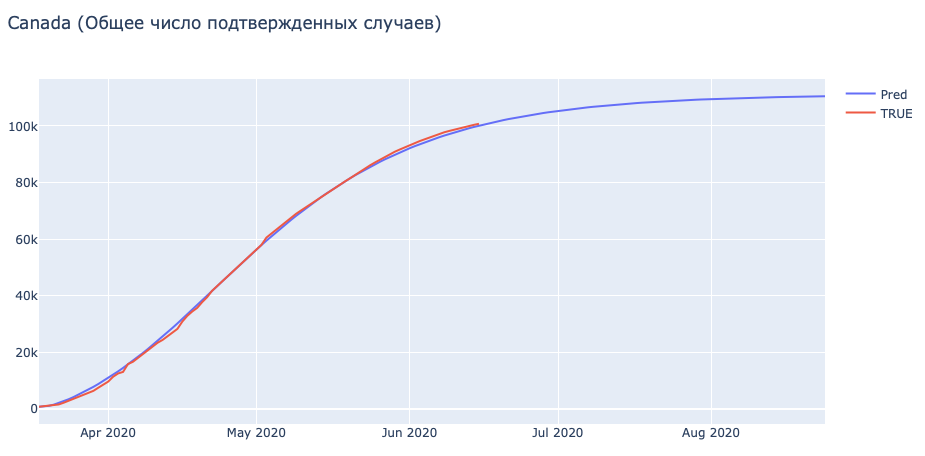
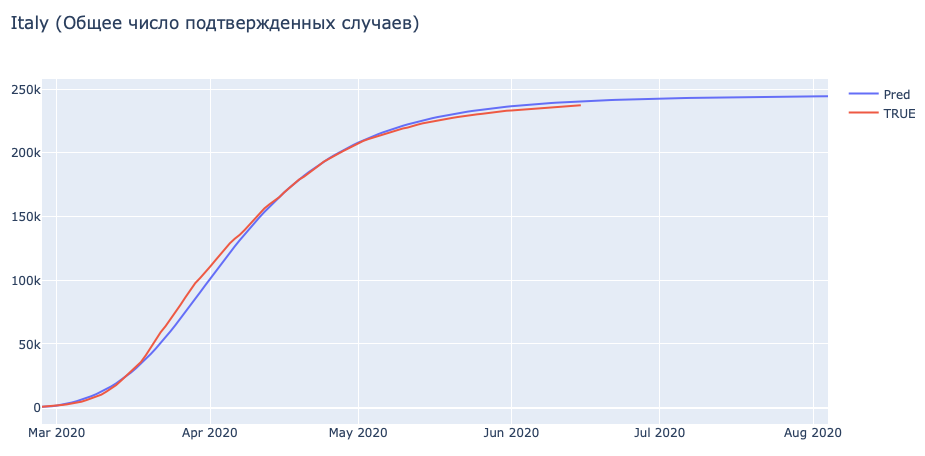
| phi | mu | c_0 | beta | theta | eta | gamma_I | gamma_A | gamma_H | d | epsilon | q_2 | q_3 | sigma | |
| Canada | 0,063 | 0,049 | 32,453 | 0,071 | 0,783 | 0,137 | 0,735 | 0,443 | 0,028 | 0,004 | 0,750 | 0,843 | 0,047 | 1,63E-05 |
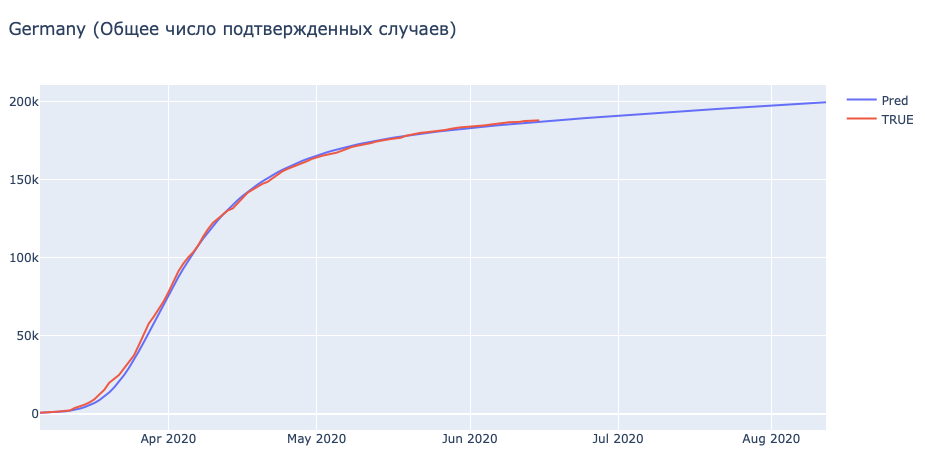
| Germany | 0,078 | 0,033 | 33,262 | 0,092 | 0,838 | 0,024 | 1,000 | 0,100 | 0,059 | 0,001 | 0,773 | 0,746 | 23,883 | 3,42E-05 |
| Italy | 0,063 | 0,083 | 33,837 | 0,129 | 0,531 | 0,004 | 0,736 | 0,486 | 0,023 | 0,005 | 0,741 | 0,602 | 8,119 | 1,36E-05 |
Вот, тут все гораздо приятнее. Параметры, которые мы получили для этих стран выглядят более правдоподобными. Так хорошо модель обучается, в том числе, из-за более точной статистики — в этих странах изменения методики подсчета походу дела, сама методика схожая и так далее.
Так же видно, что в Германии происходит ‘Немецкое Чудо’ (система здравоохранения работает практически идеально, смертность очень низкая) — поэтому некоторые параметры для Германии показывают экстремальные значения.
В целом эта модель горааааздо устойчивее к флуктуациям в статистике, хотя и не идеальна и иногда проваливается в локальные минимумы, хоть и близкие к глобальным. Можно так же заметить, что данные везде, кроме России, почти во всех странах подвержены «синдрому выходного дня», о котором упоминалось выше.
Влияние изменения параметров
Попробуем немного поиграться с параметрами и посмотрим, как вводимые меры влияют на итоговое количество переболевших. При этом остальные параметры оставим фиксированными, как они были подобраны для текущего региона (вероятность передачи, количество бессимптомные больных и прочее). (В таком формате ст.8)
Тут мы не будем концентрироваться на статистике как таковой, а только косвенно описаться на неё при проверке адекватности вариаций параметра.
Заразность
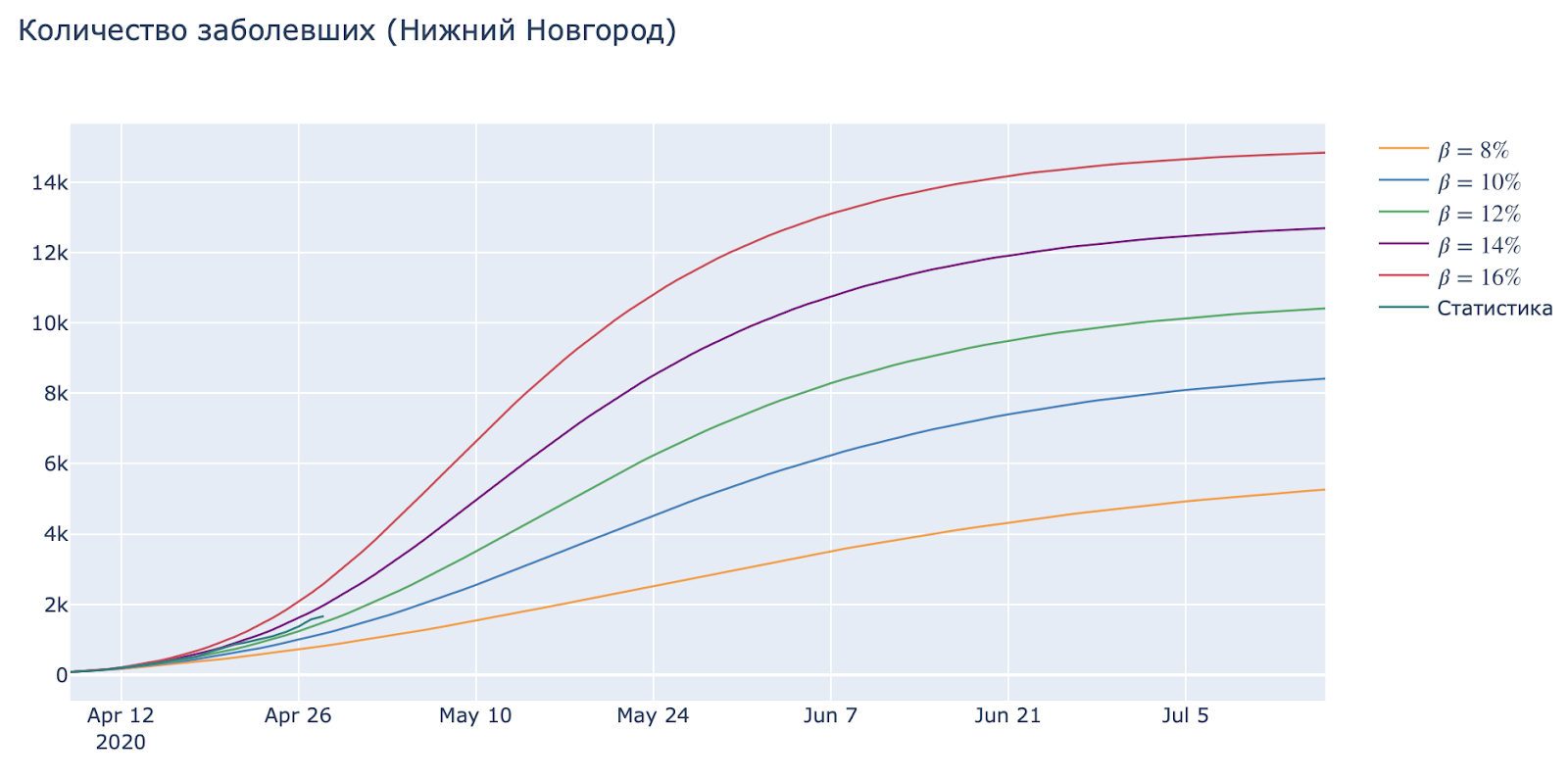
beta — вероятность передачи вируса через контакт с инфицированным, при дистанции в полтора метра. Эту вероятность можно уменьшить путем соблюдения мер предосторожности и использования средств защиты, таких как перчатки, маски, антисептики. Кроме того, чем больше магазинов, транспорта дезинфицирует свои помещения и поверхности, тем вероятность beta, предположительно, меньше.

Видно, что это довольно эффективные меры, которыми можно сильно повлиять на ситуацию в целом.
Соблюдая меры предосторожности, можно растянуть пик эпидемии, освобождая медицинскую систему от нагрузки, и, в конце концов, серьезно снизить количество заболевших.
Конечно, есть вариант переболеть быстро и всем (при этом умрет большой процент населения). В этом сценарии нужно посоветовать людям облизывать все поручни в маршрутках и почаще ходить на митинги / кафе / туристические места / храмы
Отдельные авторы пишут, что отказ от антисептиков может повышать риск ОРЗ как минимум в 1,3 раза. Оценка повышения вероятности передачи при отказе от ношения перчаток пока оценено довольно плохо. Но однозначно известно, что ослабление карантина (в разных его формах) повышает эту вероятность из-за более халатного отношения к дистанции. Социальное дистанцирование примерно в 2-3 раза снижает вероятность.
Коэффициент Страха
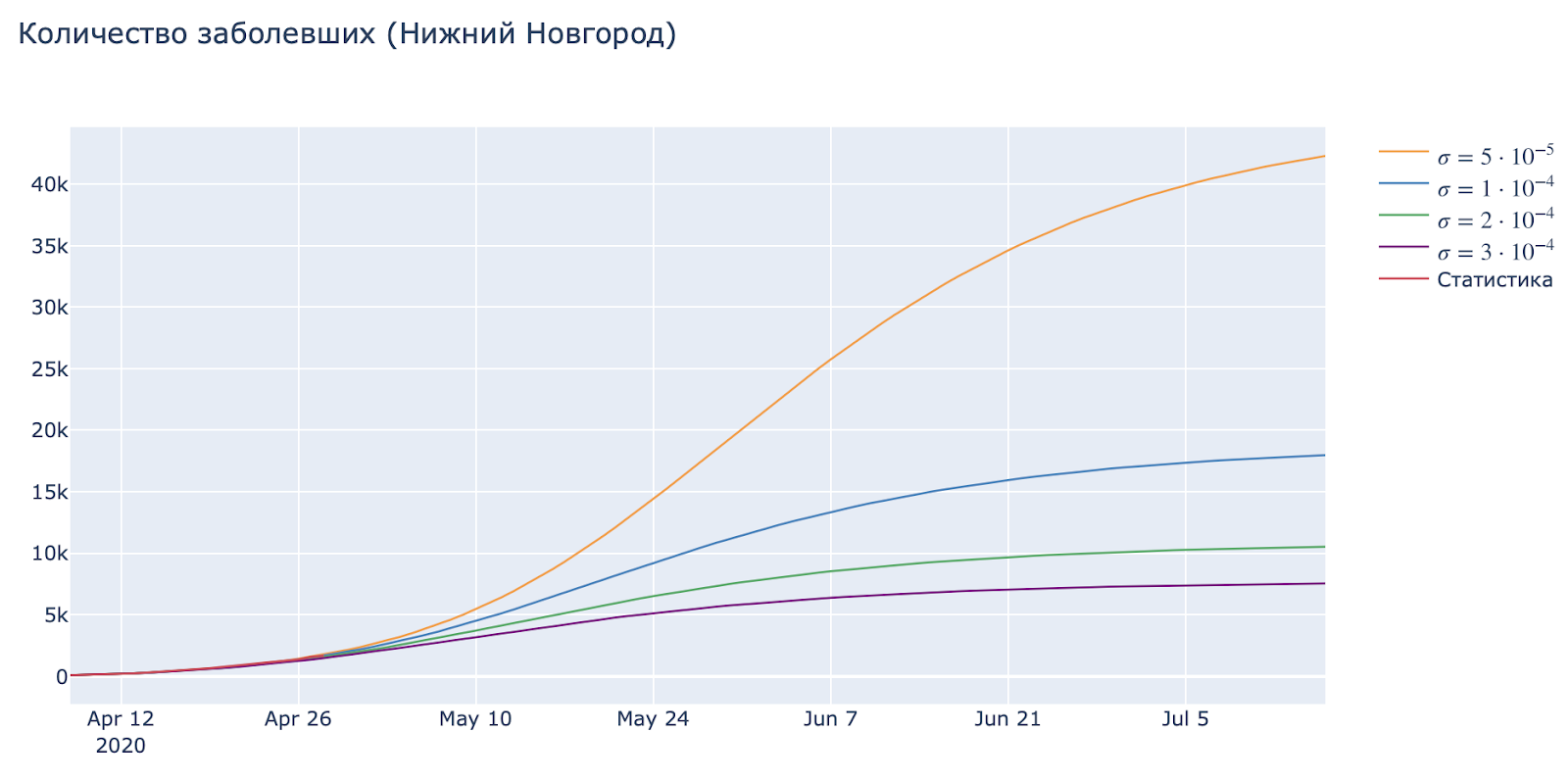
Рассмотрим изменение параметра sigma, который отвечает за снижение частоты контактов относительно кумулятивной суммы зараженных. (Проще говоря — насколько люди пугаются больших цифр по телевизору и начинают добросовестно соблюдать самоизоляцию).
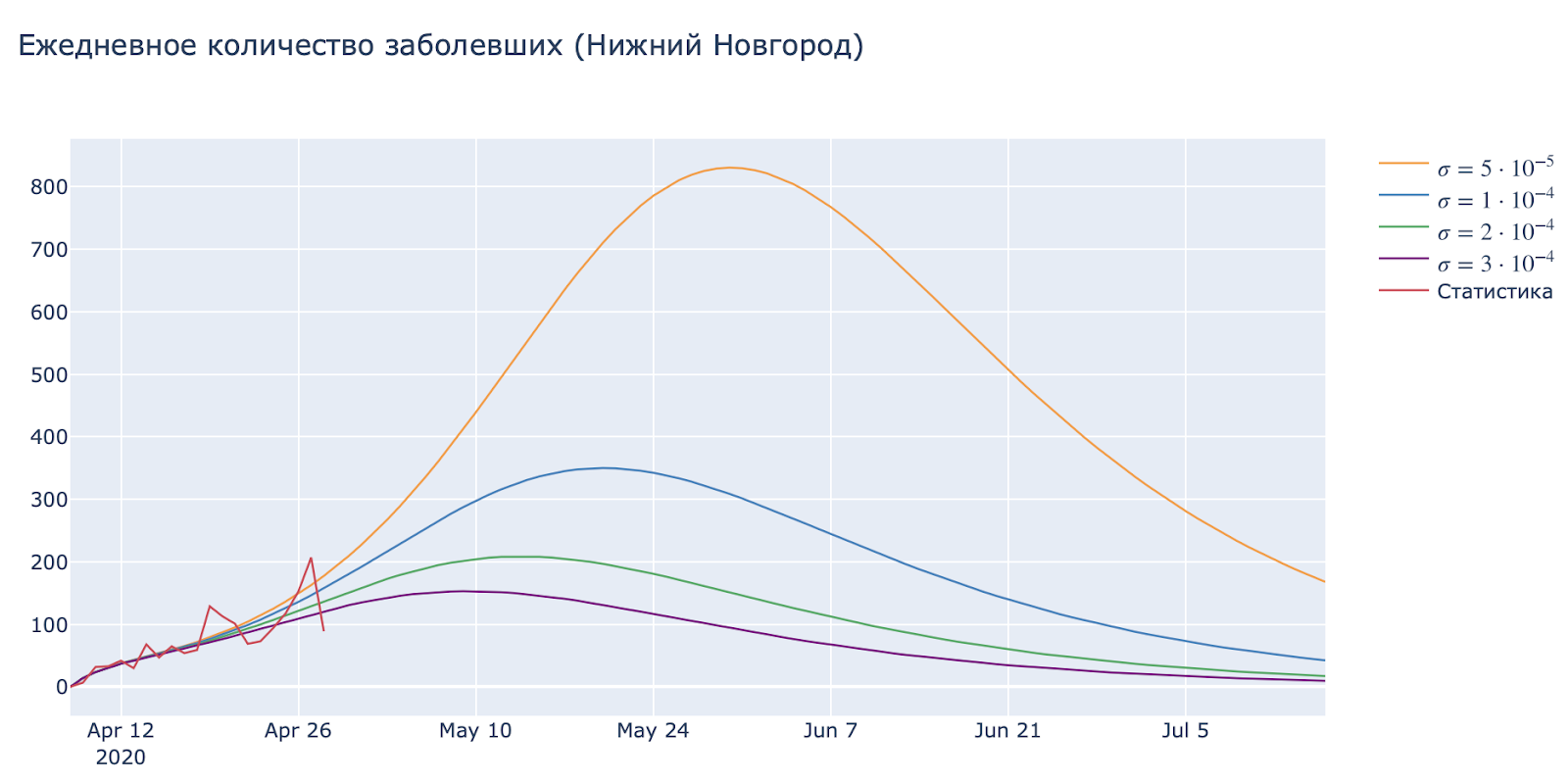
Игнорирование мер изоляции и базовых правил предосторожности ведут к увеличению количества заболевших.
Самые очевидные меры по предотвращению снижения значения данного параметра: оповещение в СМИ, в соцсетях, закрытие предприятий и так далее.
Роль бессимптомных зараженных
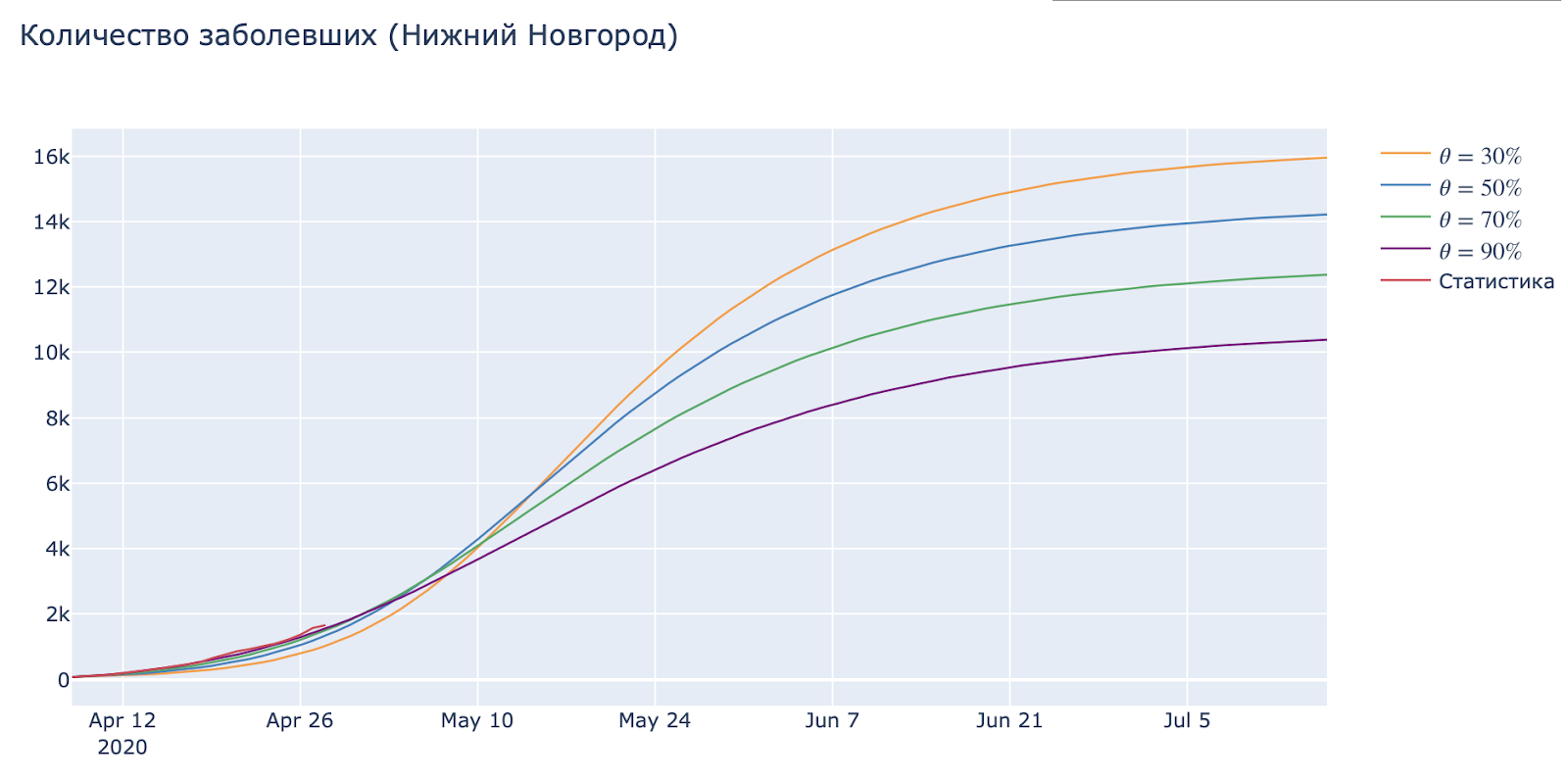
А теперь проверим, как изменяется характер эпидемии при изменении доли бессимптомных больных. Границы этого параметра мы можем изначально оценить только приблизительно, потому что для уверенного заявления нужно массовое тестирование (см. Норвегию/Корею)
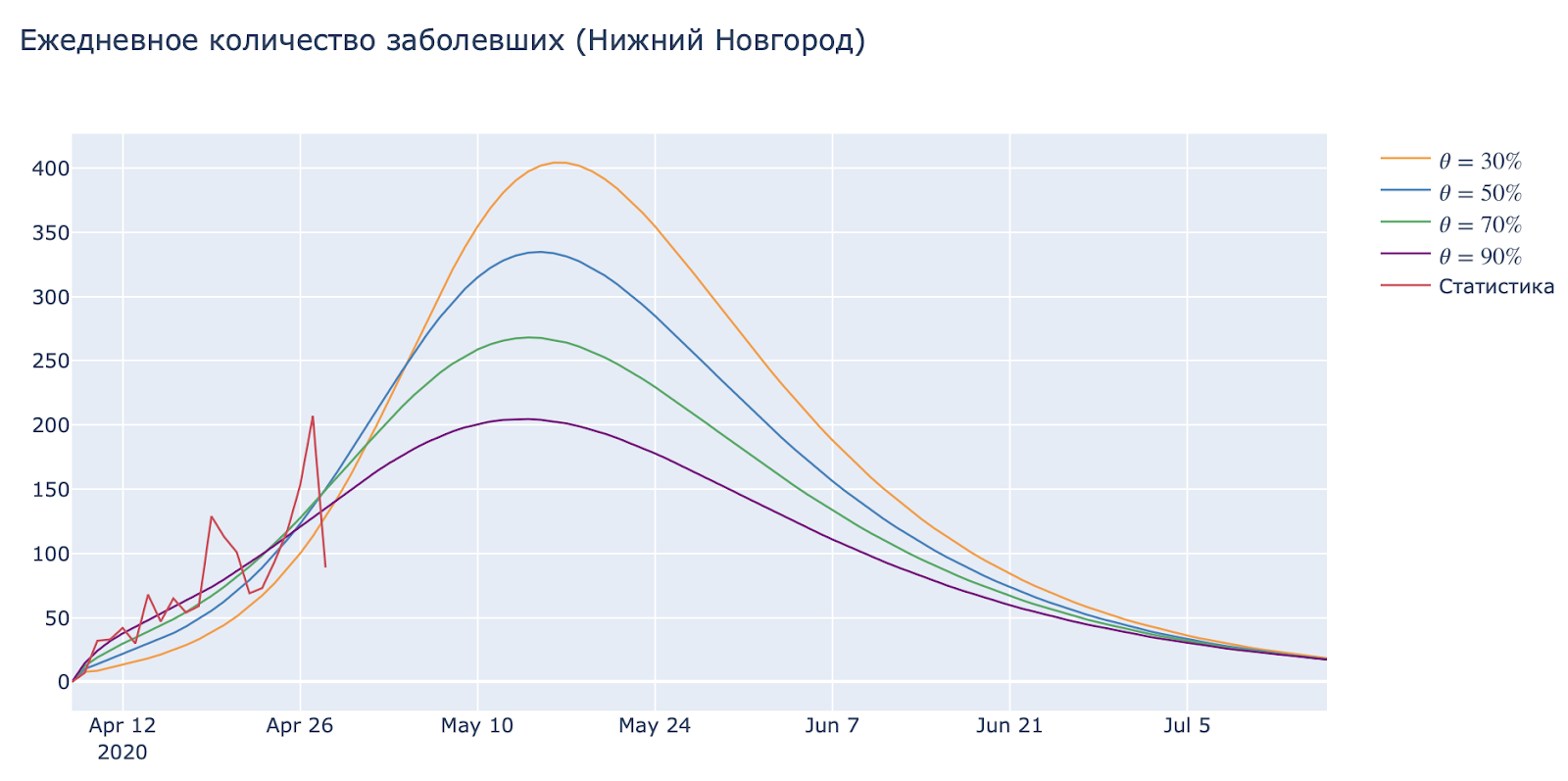
Довольно очевидно, что зараженные без выраженных симптомов дают меньший вклад в развитие эпидемии (нет кашля — меньше шанс заразить случайного прохожего рядом). Однако, очень сложно оценить не только количество асимптомных больных, но и как именно они влияют на общую картину хода эпидемии. Для этого нужно обширное проведение скрининговых исследований на антитела.
Так же довольно сильно будет влиять возрастное распределение этого параметра: молодые, в основном, болеют бессимптомно, пожилые — с осложнениями и выраженными симптомами.
А теперь перейдем к самому интересному — параметры, которые напрямую зависят от мер, введенных конкретным государством.
Массовое тестирование

На этот параметр уже напрямую влияет государство. Доступность тестов, массовое тестирование на улицах, точность тестов (ошибка первого уровня) и банальная готовность системы здравоохранения.
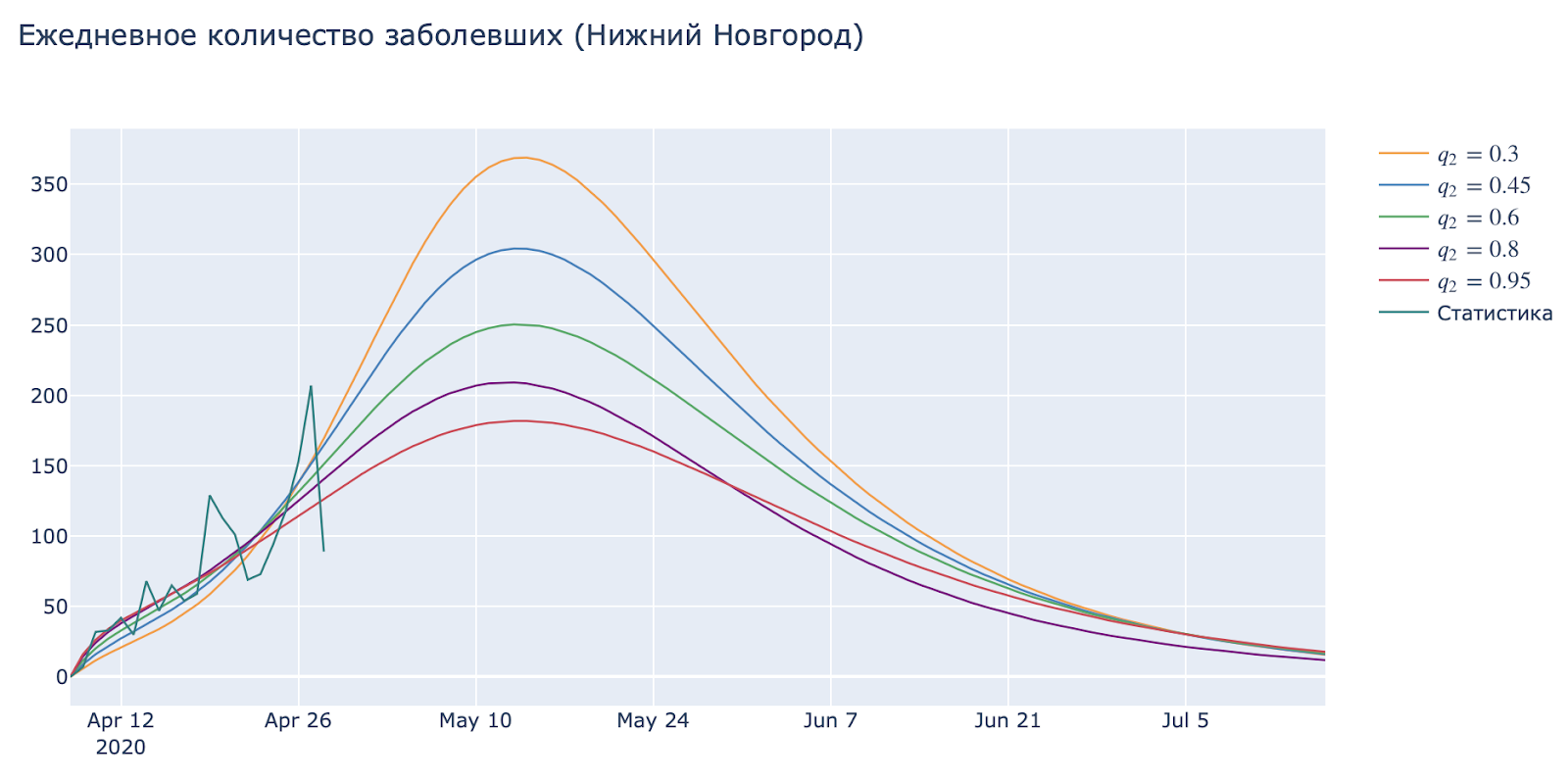
Массовое тестирование точными тестами (простите за тавтологию) помогает существенно снизить число заболевших в активной фазе, выявить большее число бессимптомных и, как следствие, изолировать больше активных переносчиков.
Можно предложить, например, такие меры: патрули на улицах, которые (не арестовывают людей и ведут их в отделение, где будет скопление народа) берут тесты у всех желающих. Крупные предприятия продолжают работу только при условии регулярной бесплатной (!) проверки сотрудников. Проверки с выездом на дом или рабочее место.
Большой Брат
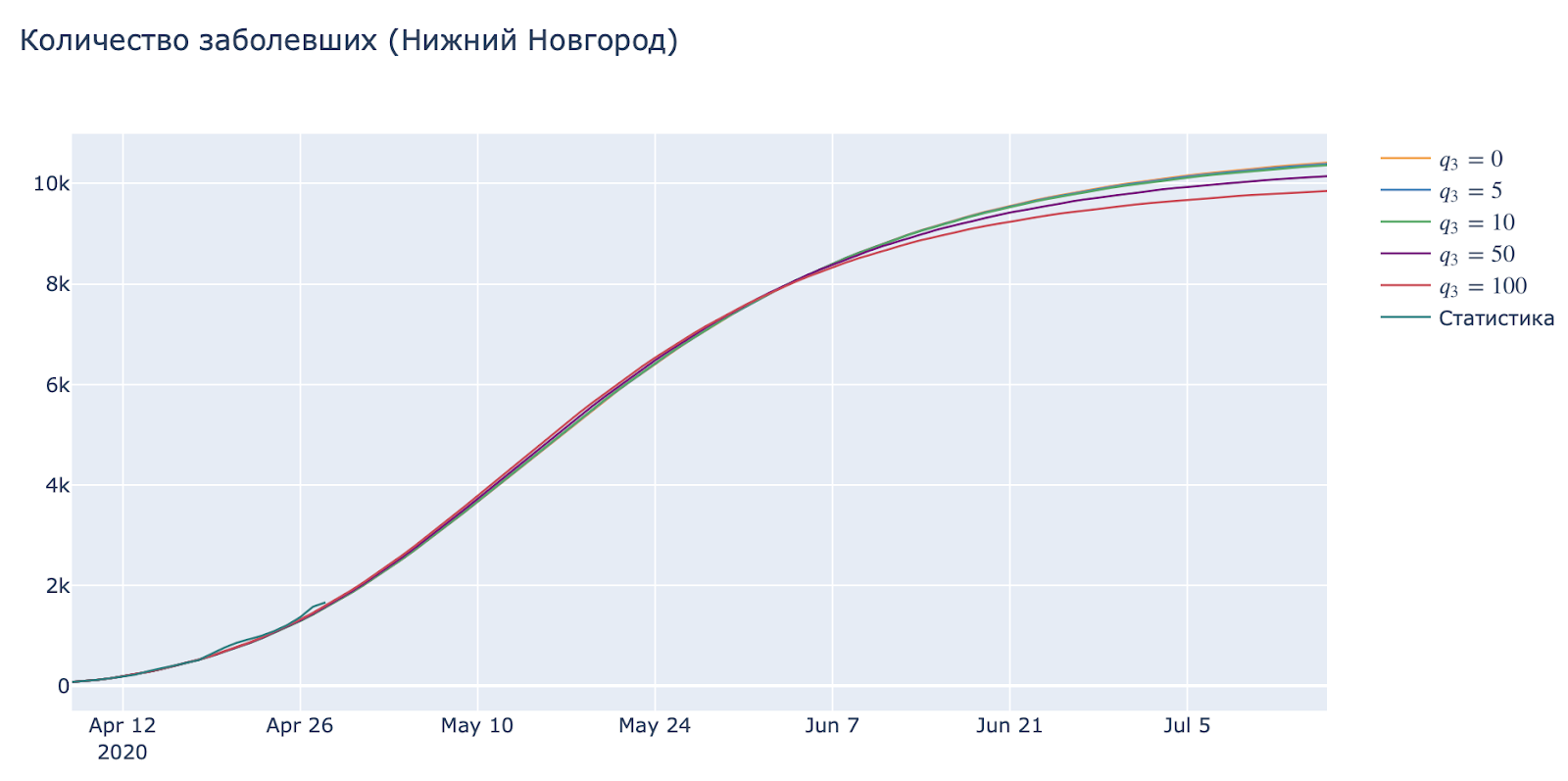
На этом месте самое время вспомнить Большого Брата из романа 1984 и его жгучее желание отслеживать контакты и перемещения всех и каждого.
Введение похожих мер во многих странах оправдывается «заботой о людях» и соблюдением карантинных мер. К сожалению, государственные организации не могут предоставить конкретных данных по работе Рос-[Контроля] в этой сфере. Однако, посмотрев на колебания данного параметра, мы можем получить качественную оценку, показывающую полную неэффективность мер такого рода.
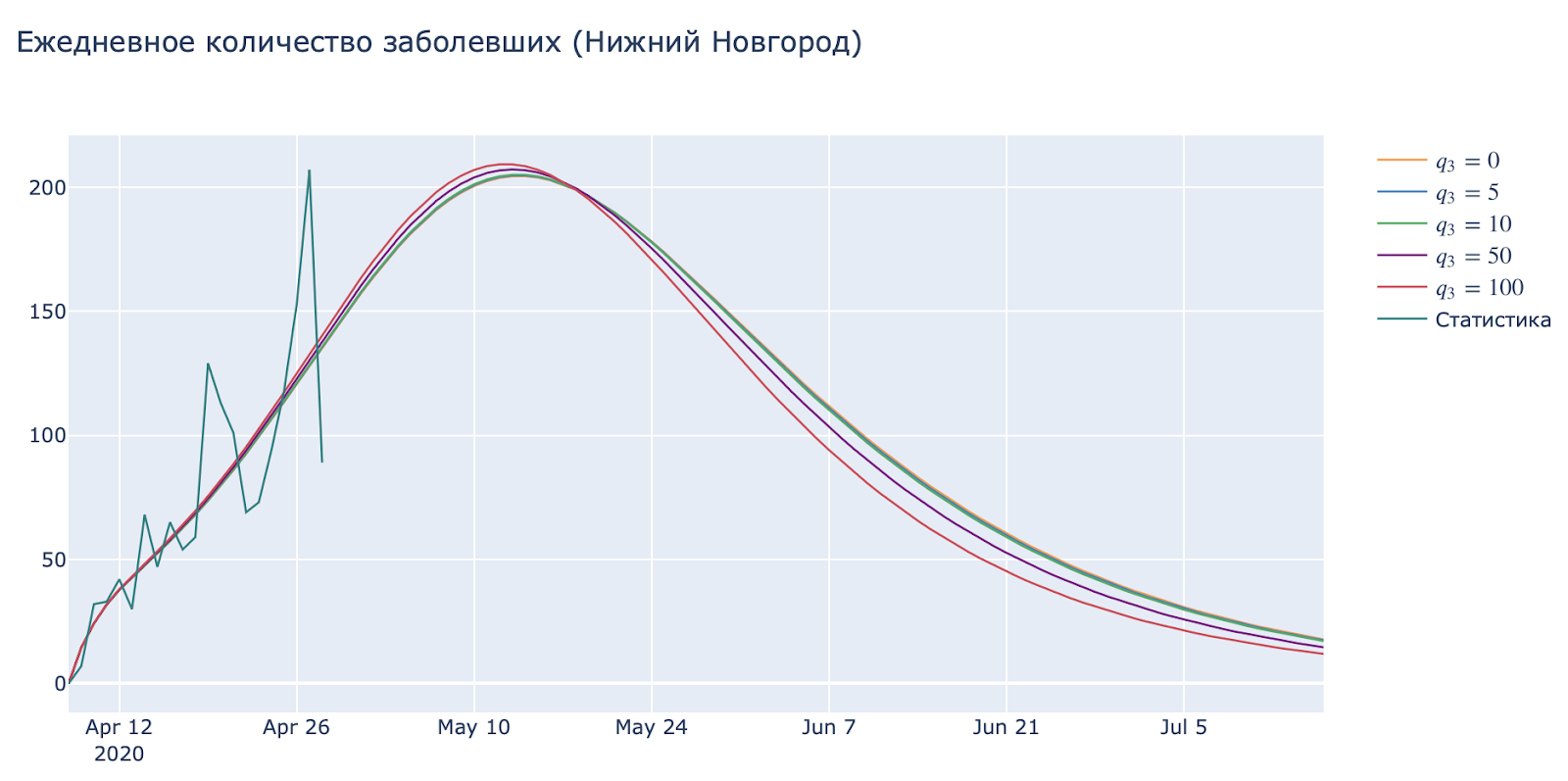
Тут можно сделать простой вывод: отследить все контакты потенциальных больных физически невозможно (см пациент 31 из Южной Кореи). Да, Google & Apple разработывают систему, но она лишь увеличит количество людей, которые захотят провериться, но не сможет уберечь их от заражения.
Область сценариев
Попробуем оценить насколько же разными может быть исход эпидемии в стране и регионе. Методика оценивания основывалась на умных книжках (например, Nonlinear Parameter Estimation — Yonathan Bard). В рамках этой статьи мы не будем залезать в матан, а только посмотрим на примерные картинки.
Естественно, итоговый результат может сильно колебаться в зависимости от введенных далее мер (или снятия оных), сознательности граждан и банальной удачи.
Для каждого региона можем найти параметры модели, которые наилучшим образом предсказывают развитие эпидемии по текущим данным. По найденным параметрам, как по случайным величинам, можно оценить интервал параметров — как будет развиваться эпидемия в любой произвольной стране.
Здесь применимы все стандартные средства матстата и статистического анализа.
Для Нижнего Новгорода было получено:
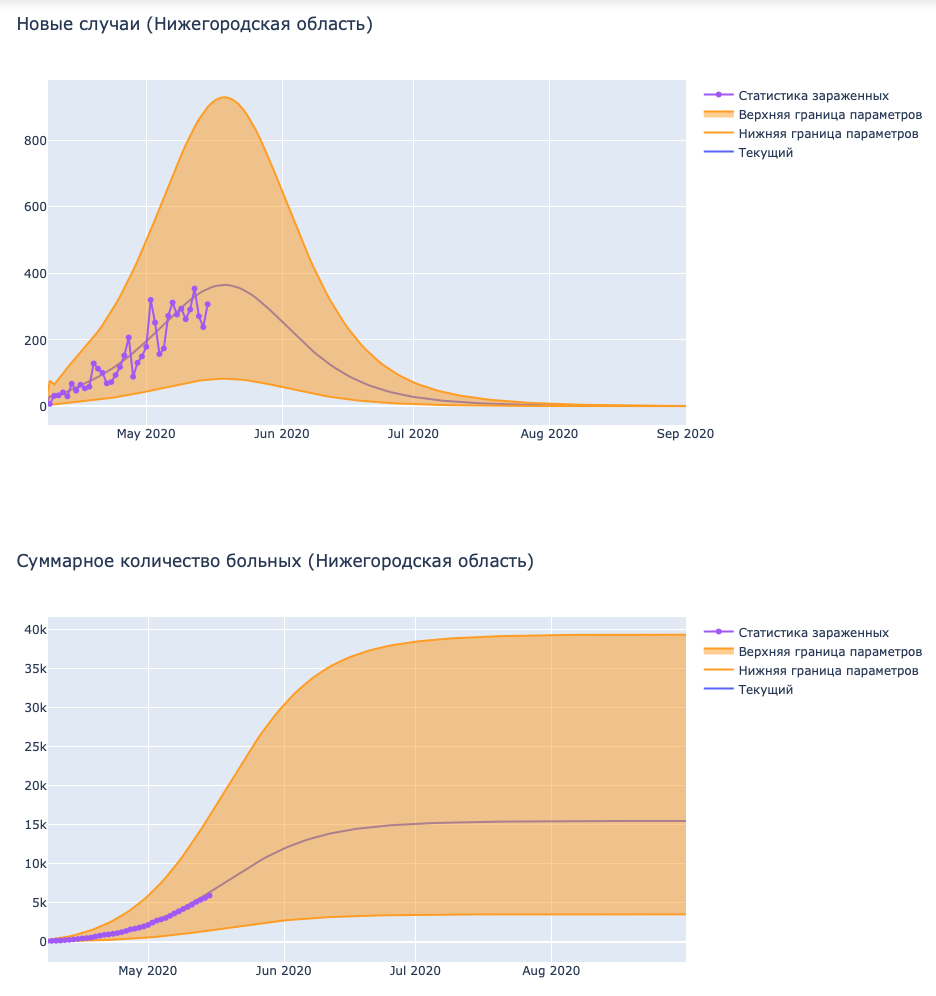
На графике, кроме интервала наиболее вероятных сценариев, так же изображено наиболее вероятное (для используемой статистики) предсказание.
Видно, что тренд может сильно меняться из-за недостаточной точности данных и большого шума в данных по регионам. Однако, прогнозы укладываются в нашу область.
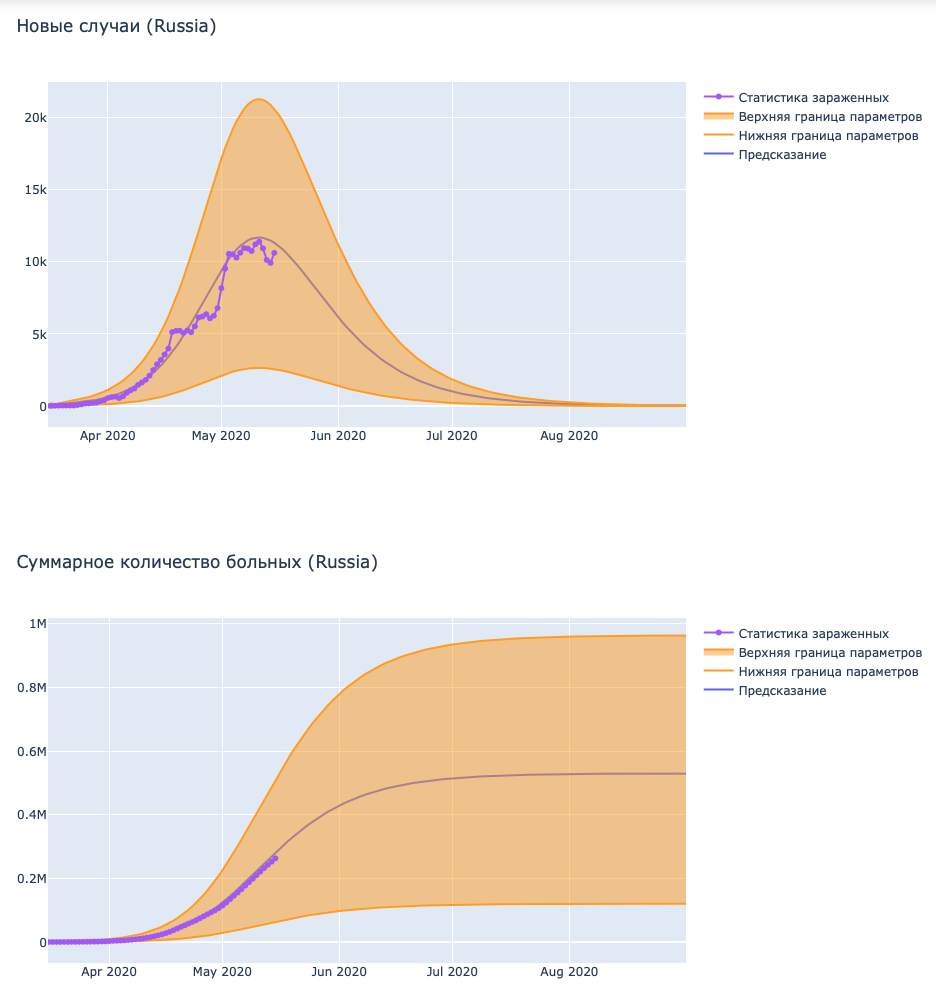
Краткие выводы
Веря официальной статистике, переболеет небольшая часть населения, при условии соблюдения мер. Еще один вывод, вытекающий из предыдущего, что «русский менталитет» помогает существенно снизить заразность вируса. Особенно в последнюю половину мая.
Для COVID-19 инкубационный период составляет от 2 до 14 дней (чаще всего 5-6), латентный период практически равен инкубационному. Поэтому, даже если вы чувствуйте себя отлично равно как и ваши друзья, с которыми вы хотите встретиться, то это не ограничит вас на 100% от заражения. А нарушением самоизоляции вы повысите beta — уровень заразности вируса в стране.
Очень сильно итоговая ситуация зависит от уровня изоляции жителей. Это связано с сознательностью, введением карантина, помощью государства, возможностью работать из дома и многим другим.

Тогда как прямая слежка за перемещением от государства практически не влияет на ход эпидемии.
В России и в мире значительная часть инфицированного населения переносит болезнь в бессимптомной форме. (в некоторых странах бОльшая часть, иначе не сходится официальная статистика и теоретические изыскания). Хотя это существенно не будет влиять на саму эпидемию.
В целом, для стран с большим доверием к статистики модель позволяет получить достаточно точный прогноз.
Отдельная благодарность kblack, pixml и keysloss за помощь в написании статьи и построении модели.