Эта статья является четвертой заключительной и самой объемной частью конспекта книги «Скрытая реальность: Параллельные миры и глубинные законы Космоса».
Платон утверждал, что наши ощущения — это не более чем слабое отражение гораздо более богатой реальности, проблёскивающей за пределами досягаемости. Похоже, что два тысячелетия спустя, пещера Платона может стать чем-то большим, чем просто метафорой.
Являясь, возможно, наиболее странной реализацией идеи о параллельных мирах, голографический принцип предполагает, что всё, что мы ощущаем, может быть полностью эквивалентным образом описано в виде нечто, происходящего на тонкой и удалённой поверхности. Он утверждает, что если было бы возможно понять законы, управляющие физикой на этой удалённой поверхности, и то, как происходящие там явления связаны с нашим опытом здесь, мы смогли бы полностью разобраться в окружающей действительности.
Информация
Традиционно физика рассматривает объекты и изучает силы, влияющие на их поведение и управляющие их взаимодействиями. Уилер полагал, что объекты — вещество и излучение — следует рассматривать как вторичные, как носителей более абстрактной и более фундаментальной сущности: информации. Уилер не утверждал, что вещество и излучение являются в том или ином смысле эфемерными; он считал, что их следует рассматривать как материальные проявления чего-то более фундаментального. Он считал, что информация — то, где частица находится, каков её спин и так далее — образует цельное ядро в сердце реальности. То, что такая информация реализуется в реальных частицах, чем-то похоже на то, как рисунок архитектора воплощается в построенном небоскрёбе. Фундаментальная информация отражена в рисунке. Небоскрёб — это всего лишь реализация заложенной в проекте архитектора информации.
С этой точки зрения, нашу вселенную можно рассматривать как информационный процессор. Он берёт информацию, касающуюся устройства вещей сейчас, и порождает информацию, характеризующую устройство вещей в следующем сейчас, и в последующем сейчас. Наши чувства улавливают этот процесс, замечая изменения окружающей среды во времени. Но окружающая среда сама является производной; она возникает из фундаментального ингредиента, информации, и развивается согласно фундаментальным правилам, законом природы.
Не известно, будет ли такая информационно-теоретическая установка доминировать в физике, как считал Уилер. Однако недавно, во многом благодаря работам физиков т’Хоофта и Сасскинда, в сознании учёных произошёл сдвиг, вызванный изучением нетривиальных вопросов, касающихся поведения информации в одном особенном экзотическом контексте: в чёрных дырах.
Черные дыры
Решение Шварцшильда показывает, что обычные тела, такие как Солнце и Земля, не сильно искривляют пространство. Это хорошо соответствовало приближённым решениям Эйнштейна, которые ему удалось найти ранее. Но Шварцшильд смог выйти за рамки приближений. Его точное решение обладало поразительным свойством: если достаточное количество массы сжать до объёма небольшого шара, то возникнет гравитационная пропасть. Пространственно-временная кривизна станет настолько экстремальной, что всё, что отважится оказаться слишком близко, будет захвачено в ловушку. Поскольку это «всё» включает свет, такие области потемнеют и станут чёрными, что явилось причиной исходного термина «чёрные звёзды». Экстремальное искривление заставит замереть на краю звезды даже время: отсюда возник другой термин — «замёрзшие звёзды». Спустя полвека Уилер сделал популярными такие звёзды как среди научной общественности, так и у любителей науки, дав им более запоминающееся имя: «чёрные дыры».
В те времена даже Эйнштейну было трудно полностью разобраться в сложной математической структуре общей теории относительности. Интенсивное сворачивание пространства и времени, уже в то время с очевидностью следовавшее из уравнений, было, по мнению Эйнштейна, слишком радикальным, чтобы быть правдой. Эйнштейн отказывался верить, что такая экстремальная конфигурация вещества является чем-то большим, чем вышедшими из-под контроля математическими манипуляциями, хоть и вытекающими из его собственных уравнений. Но всё же за прошедшие десятилетия астрономы собрали многочисленные наблюдательные данные, свидетельства относительно того, что чёрные дыры существуют и их много.
В начале 1970-х годов Уилер осознал, что если Второй закон термодинамики рассматривать применительно к окрестности чёрной дыры, то, похоже, что он перестаёт работать. Свежий взгляд на этот вопрос Бекенштейна, студента Уилера, пришёл на выручку, посеяв при этом семена возникшего впоследствии голографического принципа.
Второй закон
Энтропия изначально была введена в середине девятнадцатого столетия для количественного описания рассеяния энергии в двигателях внутреннего сгорания, но современная точка зрения такова, что энтропия является характеристикой того, насколько упорядочена или нет данная система, для того чтобы иметь такой вид, какой она имеет.
В качестве примера рассмотрим контейнер с паром и куб изо льда. Будем рассматривать только их совокупные макроскопические свойства, которые можно наблюдать или измерять, не зная при этом детального состояния составляющих их молекул. Если опустить и вынуть руку из пара, то вы перемешаете между собой миллиарды молекул, но при этом пар будет выглядеть столь же однородным, как и ранее. Но измените случайным образом положения и скорости многих молекул в куске льда, и результат вы увидите незамедлительно — кристаллическая структура льда будет разрушена. Пар, со случайно летающими по контейнеру молекулами, обладает высокой степенью беспорядка; лёд, молекулы которого расположены регулярным образом в кристаллической решётке, высоко упорядочен. Энтропия пара высока; энтропия льда низкая.
Второй закон термодинамики устанавливает, что со временем полная энтропия системы будет возрастать. Чтобы понять, почему так происходит, достаточно самых элементарных представлений о вероятности и статистике. По определению, конфигурация с высокой энтропией может реализоваться посредством большего числа микроскопических перестановок, чем конфигурация с меньшей энтропией. По мере эволюции системы она с огромной долей вероятности оказывается в состоянии с высокой энтропией, потому что, попросту говоря, таких состояний значительно больше, чем остальных.
Как только система достигает конфигурации с максимальной энтропией (подобно пару при фиксированной температуре, однородно заполняющему контейнер), то все возможности для дальнейшего увеличения энтропии оказываются исчерпанными. Поэтому более точное утверждение таково, что энтропия возрастает, пока не достигнет наибольшего значения, допускаемого системой.
Следует отметить, что Второй закон не утверждает, что энтропия не может уменьшиться, однако такое событие крайне маловероятно. Молекулы только что добавленного в чашку кофе молока могут, в результате своих случайных движений, объединиться в плавающую статуэтку Санта Клауса. Но не дождётесь. Плавающий Санта из молока имеет очень низкую энтропию. По сравнению с этим конфигурация, в которой молекулы молока однородно распределены по чашке, имеет значительно более высокую энтропию: огромное число перегруппировок по-прежнему выглядит как обычный кофе с молоком. Аналогичные рассуждения справедливы для огромного количества переходов от высокой к низкой энтропии, так что кажется, что Второй закон несокрушим.
Второй закон и черные дыры
Вернёмся теперь к взглядам Уилера на чёрные дыры. В начале 1970-х годов Уилер заметил, что, когда чёрные дыры выплывают на сцену, Второй закон начинает сдавать свои позиции. Поместите в чёрную дыру любую изучаемую вами систему. Так как ничего не может покинуть её пределы, беспорядок в системе окажется, по-видимому, навсегда исчезнувшим. Многие посчитали, что Второй закон столкнулся с достойным соперником.
Бекенштейна это не убедило. Он предположил, что энтропия не пропадает в черной дыре, а каким-то образов в нее трансформируется. Кроме того, никто не утверждал, что, поглощая материю черная дыра приводит к нарушению Первого закона термодинамики, сохранению энергии. Наоборот, уравнения Эйнштейна показывают, что при поглощении вещества чёрная дыра становится больше и тяжелее. Энергия может перераспределиться, часть из неё упадёт в чёрную дыру, а часть останется снаружи, но общее количество сохранится. Может быть эта же идея применима и к энтропии. Часть энтропии остаётся снаружи чёрной дыры, а другая часть падает внутрь, но ничего не исчезает бесследно.
Это звучит разумно, но эксперты идею не одобрили. Найденное Шварцшильдом решение и последующие разработки показывают следующее. Каким бы перемешанным и неупорядоченным не было падающее внутрь вещество и излучение, оно сжимается в бесконечно малый объём в центре чёрной дыры. По правде говоря, никто не знает, что происходит во время такого мощного сжатия, потому что экстремальная кривизна и плотность делают уравнения Эйнштейна непригодными; однако всем не кажется, что в центре чёрной дыры может быть какой-то беспорядок. А за пределами своего центра чёрная дыра — просто пустая область пространства-времени, простирающаяся до горизонта событий. Нет никаких движущихся туда-сюда молекул и атомов, поэтому перегруппировываться нечему; кажется, что чёрная дыра вообще лишена энтропии.
В 1970-х годах такая точка зрения была подкреплена так называемыми теоремами об отсутствии волос, которые на математическом языке утверждают, что чёрным дырам недостаёт отличительных характеристик. Согласно этим теоремам любые две чёрные дыры, обладающие одинаковыми массами, зарядами и угловыми моментами, неразличимы.
Затем появилось ещё более убийственное рассуждение, которое, как казалось, полностью сводило на нет идею Бекенштейна. Согласно основным положениям термодинамики между температурой и энтропией есть тесная связь. Температура — это мера усреднённого движения составных частей данного объекта. Энтропия является мерой возможных перегруппировок этих компонентов, которые с макроскопической точки зрения останутся незамеченными. Таким образом, как энтропия, так и температура зависят от совокупных свойств рассматриваемого объекта. Если рассмотреть вопрос математически, то станет ясно, что если Бекенштейн прав и чёрные дыры обладают энтропией, то у них должна быть температура. Именно это и вызвало тревогу. Любой объект с ненулевой температурой должен излучать. Если чёрная дыра обладает ненулевой температурой, то сами законы термодинамики, которые Бекенштейн хотел сохранить, говорят, что она тоже должна излучать. Но это противоречит принятому пониманию, что ничего не может вырваться из гравитационной хватки чёрной дыры. Почти все решили, что Бекенштейн ошибается. У чёрных дыр нет температуры. У них нет энтропии. В присутствии чёрных дыр нарушается Второй закон термодинамики.
Несмотря на многочисленные аргументы против, в пользу Бекенштейна говорил один замечательный результат. В 1971 году Хокинг осознал, что чёрные дыры подчиняются занятному правилу. Если черная дыра поглощает материю и излучение, то полная площадь поверхности чёрной дыры возрастает. Под «площадью поверхности» Хокинг подразумевал площадь горизонта событий каждой чёрной дыры. Если считать, что каким-то образом площадь поверхности чёрной дыры является мерой её энтропии, то возрастание площади полной поверхности может рассматриваться как рост полной энтропии. Это была очень привлекательная аналогия, но почти все считали, что сходство теоремы Хокинга о площади со Вторым законом не более чем случайность. Это положение сохранялось до того момента, пока несколько лет спустя Хокинг не сделал одно из самых важных вычислений в современной теоретической физике.
Излучение Хокинга
Поскольку квантовая механика не играет никакой роли в общей теории относительности Эйнштейна, решение Шварцшильда для чёрных дыр основывается исключительно на классической физике. Однако надлежащее рассмотрение вещества и излучения — таких частиц, как фотоны, нейтрино и электроны, которые могут переносить массу, энергию и энтропию из одного места в другое — требует продлить решение Шварцшильда в квантовую область. Это нелегко. Несмотря на достижения теории струн (а также других подходов таких как петлевая квантовая гравитация), физики по-прежнему находятся на начальном уровне в попытках совместить квантовую физику и теорию гравитации. А в далёких 1970-х было ещё меньше теоретических оснований для понимания того, как квантовая механика может влиять на гравитацию.
Однако были физики, которые работали в этом направлении и которым удалось добиться частичного объединения квантовой механики и общей теории относительности, рассмотрев распространение квантовых полей (квантовая часть) в фиксированной, но искривлённой пространственно-временной среде (гравитационная часть). Хокинг воспользовался частичным объединением и рассмотрел, как квантовые поля будут вести себя в очень особой области пространства-времени — в окрестности чёрной дыры. То, что он обнаружил, поразило физиков до глубины души.
Хорошо известное свойство квантовых полей в обычном, пустом, не искривлённом пространстве-времени состоит в том, что из-за квантовых флуктуаций парам частиц, например, электрону и его античастице, позитрону, позволяется мгновенно возникнуть из ничего, немножко пожить, после чего столкнуться друг с другом, и в результате взаимно аннигилировать. Этот процесс, квантовое рождение пары, интенсивно изучался как теоретически, так и экспериментально, и был разобран со всех сторон.
Новой характеристикой квантового рождения пары является то, что если один партнёр имеет положительную энергию, то из закона сохранения энергии следует, что другой партнёр должен обладать тем же количеством отрицательной энергии — понятие, которое не имеет смысла в классической вселенной. Однако, благодаря принципу неопределённости имеется своеобразная лазейка, позволяющая частицам иметь отрицательную энергию. Если частица существует лишь мимолётно, то квантовая неопределённость говорит, что никакому эксперименту не хватит времени, даже в принципе, определить знак её энергии.
Хокинг заново рассмотрел вездесущие квантовые флуктуации, но не в пустом пространстве, а вблизи горизонта событий чёрной дыры. Если частицы образуются достаточно близко к краю чёрной дыры, то одну из них может затянуть внутрь, а другая улетит в пространство. В отсутствии чёрной дыры такого никогда не происходит, потому что, если частицы не аннигилируют друг с другом, то частица с отрицательной энергией сможет пробиться сквозь защитную рябь квантовой неопределённости. Хокинг осознал, что столь радикальное закручивание пространства и времени чёрной дырой может привести к тому, что частицы, обладающие отрицательной энергией с точки зрения наблюдателя снаружи чёрной дыры, окажутся частицами с положительной энергией для наблюдателя внутри неё. Таким образом, чёрная дыра предоставляет частицам с отрицательной энергией надёжное убежище, поэтому нужда в квантовой маскировке отпадает.
Причина, по которой энергия меняется, отнюдь не так очевидна; она основывается на внутренней связи между энергией и временем. Энергию частицы можно представлять, как скорость вибраций квантового поля. Если заметить, что сам смысл скорости вовлекает понятие времени, взаимосвязь между энергией и временем становится очевидной. Чёрные дыры оказывают глубочайшее влияние на время. Для удалённого наблюдателя время при приближении объекта к горизонту чёрной дыры замедляется, а на горизонте останавливается совсем. При пересечении горизонта время и пространство меняются ролями — внутри чёрной дыры радиальное направление становится временем. Это означает, что внутри чёрной дыры понятие положительной энергии совпадает с движением вдоль радиального направления к центру сингулярности чёрной дыры. Когда партнёр с отрицательной энергией из пары рождённых из вакуума частиц пересекает горизонт, он действительно падает в центр чёрной дыры. Таким образом, отрицательная энергия, которая у него была с точки зрения удалённого наблюдателя, становится положительной энергией для наблюдателя внутри чёрной дыры. Поэтому такие частицы могут существовать во внутренности чёрной дыры.
Частицы с положительной энергией летят наружу от горизонта событий, поэтому издалека они выглядят как некое излучение, получившее название излучение Хокинга. Частицы с отрицательной энергией поглощаются чёрной дырой, поэтому их нельзя непосредственно наблюдать, однако их можно обнаружить косвенным способом. Подобно тому как масса чёрной дыры растёт при поглощении всего, что обладает положительной энергией, она также уменьшается при поглощении всего, что имеет отрицательную энергию. Чёрная дыра излучает направленный наружу поток излучения по мере того как её масса уменьшается. То есть, если добавить квантовую механику, то чёрные дыры перестают быть абсолютно чёрными. Открытие Хокинга было как гром среди ясного неба.
Однако это вовсе не означает, что типичная чёрная дыра нагрета до красного свечения. По мере того как поток частицы летит от чёрной дыры, он должен преодолевать невероятное сопротивление со стороны её гравитационного притяжения. На это частицы тратят свою энергию и поэтому значительно остывают. Хокинг вычислил, что наблюдатель, находящийся достаточно далеко от чёрной дыры, обнаружит, что температура остаточного «утомлённого» излучения обратно пропорциональна массе чёрной дыры. Огромная чёрная дыра, подобная находящейся в центре нашей Галактики, имеет температуру менее триллионной доли градуса выше абсолютного нуля. Чёрная дыра с массой Солнца будет иметь температуру меньше чем миллионная доля градуса.
Теоретические вычисления Хокинга, определяющие температуру данной чёрной дыры и испускаемого ею излучения, дали все необходимые данные для определения количества энтропии, которую, согласно стандартным законам термодинамики, должна иметь чёрная дыра. Полученный ответ оказался пропорционален площади поверхности чёрной дыры, как и предполагал Бекенштейн.
Открытия Бекенштейна и Хокинга выявили, что в любой ситуации полная энтропия возрастает, если при этом учитывать не только энтропию обычного вещества и излучения, но также и находящуюся внутри чёрных дыр и определяемую площадью их полной поверхности.
Это заключение вызвало долгожданное облегчение. Для многих физиков Второй закон, основанный на, казалось бы, неоспоримых статистических рассуждениях, стал священным как практически никакой другой в науке. Его воскрешение означало, что с этим миром опять всё в порядке. Но со временем появилась небольшая, но первостепенно важная задача, которая показала, что вопрос о справедливости Второго закона не является самым приоритетным. Это задача о месте хранения энтропии, важность которой станет очевидной, когда мы выявим глубокую связь между энтропией и информацией.
Энтропия и скрытая информация
До настоящего момента энтропия образно описывалась как мера беспорядка, и более количественно, как число перегруппировок компонент системы, не меняющих её совокупных макроскопических свойств. Теперь можно сказать определённо, что энтропию можно осмыслить как измерение информационного разрыва между теми данными, которые у нас есть (общими макроскопическими свойствами), и теми данными, которых нет (конкретным устройством системы на микроскопическом уровне).
В качестве иллюстрации представим, что по полу разбросанно 1000 монет, часть из которых лежит вверх решкой, а часть вверх орлом. Для двух монет имеются четыре возможные конфигурации: (орёл, орёл), (орёл, решка), (решка, орёл), и (решка, решка) — две возможности для первой монеты умножаются на две для второй. Для тысячи монет число возможностей вычисляется аналогично: множитель 2 для каждой монеты, и получаем число 21000. Подавляющее большинство конфигураций орёл-решка не будут обладать особыми свойствами, поэтому они никак не будут выделены среди прочих.
Для установления более глубокой связи между энтропией и информацией необходимо уточнить картину, описанную выше. Энтропия системы связана с числом неразличимых перегруппировок её компонентов, но, строго говоря, не равна ему. Эта взаимосвязь выражается с помощью математической операции, называемой логарифмом. Это означает, что в качестве энтропии надо взять показатель полученного нами числа конфигураций, то есть энтропия определяется как 1000, а не 21000.
Преимущество использования логарифма в том, что он позволяет работать с более обозримыми числами, но есть и более важная причина. Чем на самом деле является информация и для чего она нужна? Годы исследований по физике, математике и компьютерным технологиям сделали этот ответ точным. Эти исследования установили, что наиболее полезная мера содержания информации — это число различных «да или нет» вопросов, на которые у этой информации есть ответ. Элемент данных, который может содержать ответ на «да или нет» вопрос, называется битом — двоичный символ, означающий 0 или 1, о котором можно думать, как о численном представлении ответов да или нет. Таким образом, конфигурации орёл-решка из 1000 монет содержат 1000 бит информации.
Мы рассмотрели частный пример с 1000 монетами, но установленная связь между энтропией и информацией имеет совершенно общий характер. Микроскопические детали любой системы содержат информацию, которая скрыта только при рассмотрении макроскопических свойств. Например, вы знаете температуру, давление и объём контейнера с паром, но известно ли вам, ударялась ли молекула о верхний правый угол этого контейнера? Так же как с разбросанными монетами, энтропия системы равна числу «да или нет» вопросов, ответы на которые содержатся в её микроскопическом состоянии, и поэтому энтропия является мерой, скрытой в системе информации.
Энтропия, скрытая информация и черные дыры
Когда Хокинг разработал детальное квантово-механическое обоснование, связывающее энтропию чёрной дыры с площадью её горизонта событий, он не только дал количественное описание исходного утверждения Бекенштейна, но также создал алгоритм для его вычисления. Хокинг математически доказал, что энтропия чёрной дыры равна числу клеток планковсой длины, которым покрывается весь горизонт событий — иными словами, это площадь поверхности чёрной дыры, измеренная в планковских единицах. На языке скрытой информации всё выглядит так, как будто каждая клетка тайным образом несёт один бит, 0 или 1, что даёт ответ на один вопрос, описывающий какую-то характеристику чёрной дыры на микроскопическом уровне.
Однако полученные результаты привели к новым вопросам. Хотя Бекенштейн и Хокинг говорят нам, сколько информации скрыто в чёрной дыре, нам ничего не известно о том, что это за информация. Математический анализ точно определил величину информации данной чёрной дыры, ничего не сообщив о природе этой информации.
Но есть и другая загадка, которая видится ещё более важной: почему количество информации определяется площадью поверхности чёрной дыры? Если бы вы спросили, сколько информации содержится в библиотеке, логично было бы начать говорить о доступном пространстве внутри здания библиотеки. Однако удивительно, что применительно к чёрным дырам способность для хранения информации определяется, согласно Бекенштейну и Хокингу, не объёмом, а площадью поверхности.
Так впервые возникло указание на голографию —вместимость информационного хранилища определяется площадью граничной поверхности, а не объёмом находящегося внутри неё пространства.
Где находится скрытая информация черной дыры?
Если математика говорит, что информационный запас чёрной дыры измеряется площадью её поверхности, то является ли это просто средством численного подсчёта, или же это означает, что поверхность чёрной дыры и есть место фактического хранения информации?
Этот глубокий вопрос десятилетиями изучался самыми знаменитыми физиками. Ответ на него в сильной степени зависит от того, смотрите вы на чёрную дыру снаружи или изнутри — если снаружи, то есть веская причина полагать, что информация действительно находится на горизонте.
Однако ОТО со всей ясностью говорит, что при падении сквозь горизонт событий чёрной дыры ничего особенного не происходит — нет никакой материальной поверхности, нет ничего, что каким бы то ни было образом отметило пересечение границы невозврата. Согласно ОТО наши чувства не смогут отличить падение от плавания в пустом пространстве. Это означает, что не будет происходить ничего особого или необычного, пока вы свободно падаете сквозь горизонт чёрной дыры. В конце концов, вы ударитесь о центр чёрной дыры, свободное падение прекратится и здесь ваши чувства, несомненно, это зафиксируют.
Этот сюжет придаёт энтропии чёрной дыры ещё больше загадочности. Если при пересечении горизонта чёрной дыры вы ничего не обнаруживаете, ничего отличающего горизонт от внешнего пространства, то как он может хранить информацию? Ответ, к которому тяготеют учёные в течение последнего десятилетия, перекликается с темой дуальности. Дуальность возникает в ситуациях, где есть взаимодополнительные точки зрения, кажущиеся совершенно разными, но при этом внутреннее скованные единой физической цепью.
Одна существенная точка зрения принадлежит вам, свободно падающему в чёрную дыру. Другая принадлежит удалённому наблюдателю, следящему за вашим путешествием в телескоп. По мере того как вы пересекаете горизонт чёрной дыры, удалённый наблюдатель видит совершенно иную последовательность событий. Всё дело в излучении Хокинга. Когда удалённый наблюдатель измеряет температуру излучения Хокинга, он обнаруживает, что она очень мала. Однако удалённый наблюдатель знает, что излучение холодное лишь потому, что идущие к нему от горизонта фотоны истратили много своей энергии, преодолевая гравитационное притяжение чёрной дыры. Наблюдатель приходит к выводу, что при вашем приближении к горизонту чёрной дыры вы будете встречать всё более энергичные фотоны, которые только начали своё путешествие. Действительно, наблюдатель видит, как вы, подойдя на волосок к горизонту, облучаетесь всё более и более интенсивным излучением Хокинга, до тех пор, пока от вас не останутся лишь обугленные останки. К счастью, ваши ощущения гораздо более приятные. Вы не видите, не ощущаете и вообще никак не знаете о существовании этого горячего излучения. Опять же, поскольку состояние свободного падения нейтрализует действие гравитации, ваши ощущения неотличимы от плавания в пустом пространстве. Поэтому с вашей точки зрения вы удачно проходите сквозь горизонт и (менее удачно) сваливаетесь в сингулярность чёрной дыры, а с точки зрения удалённого наблюдателя вы сгораете в пылающей короне, окружающей горизонт.
Какая из этих двух точек зрения правильная? Физики утверждают, что обе. Безо всяких сомнений, это трудно совместить с обычной логикой — логикой, согласно который вы либо живой, либо нет. Но это не обычная ситуация. Даже больше, эти две столь разные точки зрения никогда нельзя будет сопоставить. Вы не сможете выбраться из чёрной дыры и доказать удалённому наблюдателю, что живы. И, как оказывается, удалённый наблюдатель не может прыгнуть в чёрную дыру и озадачить вас утверждением, что вас больше нет. Удалённый наблюдатель, внимательно изучая дошедшее до него излучение, может восстановить историю вашей гибели в огне. Но требуется время, чтобы эта информация достигла его. Математические расчёты показывают, что к тому моменту, когда он сможет сделать вывод, что вы сгорели, у него не останется достаточно времени прыгнуть в чёрную дыру и поймать вас прежде, чем вас поглотит сингулярность.
Что насчёт информации? С вашей точки зрения вся информация, хранящаяся в вашем теле и голове, проходит вместе с вами сквозь горизонт чёрной дыры. С точки зрения удалённого наблюдателя вся переносимая вами информация поглощается слоем излучения, непрерывно клубящимся вблизи горизонта. Биты, содержащиеся в вашем теле, могут сохраниться, но при этом совершенно перемешаются после столкновения и смешения с обжигающе горячим горизонтом. Поэтому для удалённого наблюдателя горизонт событий является реальным местом, населённым реальными вещами, физическими носителями информации.
Вывод такой, что удалённый наблюдатель заключает, что энтропия чёрной дыры определяется площадью её горизонта, потому что горизонт является местом её хранения.
За пределами черных дыр
Результаты Бекенштейна и Хокинга гласят, что скрытая информация чёрной дыры задаётся площадью её горизонта событий. Более того горизонт событий чёрной дыры совпадает с границей данной области и энтропия чёрной дыры равна площади окружающей эту область поверхности. Таким образом, мы получаем важный результат: количество информации внутри некоторой области пространства, хранящейся в любых объектах любой формы, всегда меньше площади окружающей эту область поверхности (измеренной в планковских единицах).
Всё же, если задумываться об устройстве Вселенной, ограничения информационной ёмкости говорят о многом. Представьте любую область пространства, например, комнату. Представьте, что всё происходящее в этой области сводится к некоторым информационным процессам — информация об устройстве окружающей среды в данный момент трансформируется посредством физических законов в информацию об устройстве окружающей среды через секунду, минуту или через час. Поскольку наблюдаемые нами физические процессы, а также процессы, которые нами управляют, по всей видимости, происходят внутри данной области, то естественно ожидать, что переносимая этими процессами информация также находится внутри этой области. Но только что полученные результаты предлагают альтернативный взгляд. Обнаруженная связь между информацией и площадью поверхности чёрной дыры выходит далеко за рамки простого численного расчёта; есть конкретный смысл, в котором информация хранится на поверхности чёрной дыры. Сасскинд и т’Хоофт указали, что данное рассуждение имеет совершенно общий характер: поскольку информация, необходимая для описания физических явлений внутри любой заданной области пространства, может быть полностью представлена данными на окружающей её поверхности, то существует причина думать, что эта поверхность и является тем местом, где происходят фундаментальные физические процессы. Как предлагают учёные, привычная нам трёхмерная реальность связана голографической проекцией с удалёнными двумерными физическими процессами.
Наш опыт здесь и удалённая реальность там образуют крепкую связку параллельных миров. Явления в этих двух мирах — автор книги называет их голографическими параллельными вселенными — настолько полно связаны друг с другом, что происходящие в каждом из них будут так же крепко связаны, как вы и ваша тень.
Мелким шрифтом
Как можно быть уверенным в справедливости голографического принципа? Действительно ли чёрные дыры обладают ненулевой температурой и энтропией, и если так, согласуются ли эти значения с теоретическими предсказаниями? Действительно ли информационная ёмкость некоторой области пространства определяется количеством информации, которая может быть размещена на окружающей её поверхности? И для такой поверхности является ли один бит на одну планковскую клетку пределом на самом деле? Физики думают, что ответ на каждый из этих вопросов положительный, потому что есть непротиворечивая, совместимая и аккуратно выстроенная теоретическая система, с которой такие выводы прекрасно согласуются. Но поскольку ни одна из этих идей не ложилась под экспериментальный скальпель, вполне возможно, что будущие открытия убедят ученых, что один или более из этих существенных промежуточных шагов являются неверными.
Физикам ещё предстоит создать общую схему рассмотрения этих вопросов. Считая, что как гравитация, так и квантовая механика играют центральную роль в подобных рассуждениях, можно было бы ожидать, что возможная модель для теоретических исследований данных вопросов появится в теории струн. Однако, когда т’Хоофт сформулировал голографический принцип, он стал сомневаться, что теория струн поможет в развитии этой области, заметив, что «на планковских расстояниях природа гораздо более безумна, чем могут себе представить струнные теоретики». Менее чем десятилетие спустя струнная теория доказала, что т’Хоофт ошибался, но его идеи верны.
Теория струн и голография
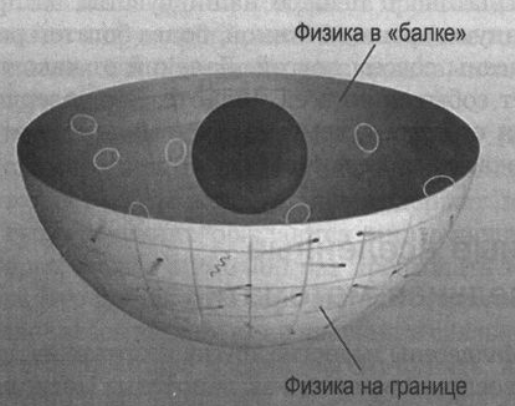
Одним из следствий результата струнного теоретика Малдасены было то, что в некотором модельном варианте его результат явно выражал голографический принцип, давая первый математический пример голографических параллельных вселенных. Для этого Малдасена рассмотрел теорию струн во вселенной, которая отличается по форме от нашей Вселенной, но которую было легче анализировать для поставленных целей. Математически отличие состояло в том, что у вселенной была граница — непроницаемая поверхность, полностью охватывающая внутренность пространства. Сосредоточившись на граничной поверхности, Малдасена убедительно доказал, что всё, происходящее внутри этой особой вселенной, является отражением действующих на границе законов и процессов.
И хотя метод Малдасены не применим, скорее всего, напрямую ко вселенной с нашей формой, этот результат имел решающее значение, потому что благодаря этому появился прямой математический способ количественного анализа идей, касающихся голографических вселенных.
Идея Малдасены состояла в использовании новой версии дуальности. Малдасена рассмотрел с двух дополнительных точек зрения свойства плотной стопки трёхмерных бран (речь идет о бранах их М-теории).
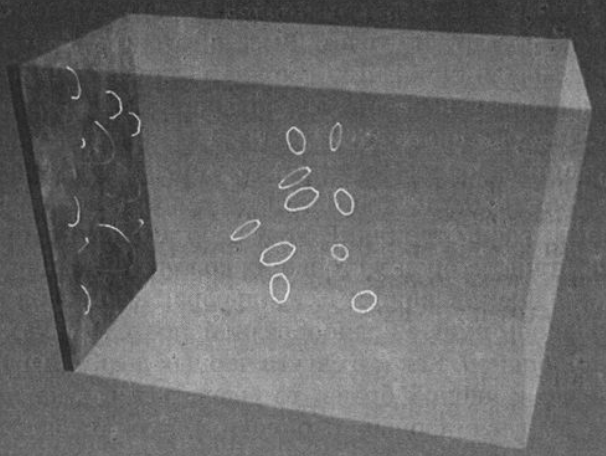
С одной, «внутренней» точки зрения, рассматриваются струны, которые движутся, вибрируют и извиваются вдоль этих бран. С другой, «внешней», точки зрения рассматривается, какое гравитационное воздействие браны оказывают на своё непосредственное окружение. Малдасена показал, что обе точки зрения описывают одну и ту же физическую ситуацию, но с разных сторон. Внутренняя точка зрения рассматривает движение струн на стопке бран, а внешняя точка зрения рассматривает движение струн в области искривлённого пространства, ограниченного стопкой бран. Приравнивая обе точки зрения, Малдасена обнаружил явную связь между физикой внутри области с физикой на границе области — была найдена подробная реализация голографии. В этом состоит основная идея.
Для тех, кому интересно более подробное описание идей Малдасона.
Рассмотрим, говорит Малдасена, стопку из три-бран, настолько близко расположенных друг к другу, что они выглядят как монолитная плита, и изучим поведение движущихся в этой среде струн. Вспомним, что есть два типа струн — открытые, как кусочки ниточек, и замкнутые, как колечки. Вспомним также, что концы открытых струн могут скользить по бранам, но не могут отрываться от них, а замкнутые струны не имеют концов и поэтому могут свободно перемещаться по всему пространству. На теоретико-струнном жаргоне мы говорим, что открытые струны прикреплены к бранами, а замкнутые струны могут двигаться по всему объёму пространства (или в «балке»).
Сначала Малдасена математически проанализировал струны с низкой энергией — то есть струны, вибрирующие относительно медленно. И вот почему: сила гравитации между двумя любыми объектами пропорциональна массе каждого объекта; это же справедливо для гравитационного притяжения между любыми двумя струнами. Струны с низкой энергией обладают малой массой и поэтому практически не реагируют на гравитационное притяжение. Таким образом, сфокусировавшись на низкоэнергетических струнах, Малдасена пренебрёг влиянием гравитации. Это стало существенным упрощением. В теории струн гравитационное взаимодействие переносится замкнутыми струнами. Поэтому пренебречь силой гравитации эквивалентно пренебречь влиянием замкнутых струн на всё, с чем они могут встретиться, — в особенности, с живущими на стопке из бран ниточками открытых струн. Таким образом, добившись, что два типа струн, открытые и замкнутые, не оказывают влияния друг на друга, Малдасена добился того, что их можно анализировать по отдельности.
Затем Малдасена изменил точку зрения и стал анализировать ту же самую ситуацию под другим углом. Вместо того чтобы считать три-браны вместилищем для движения открытых струн, он рассмотрел три-брану как самостоятельный объект, у которого есть присущая ему масса и который, таким образом, искривляет вокруг себя пространство и время. Малдасене повезло, потому что к тому времени другими физиками были уже получены результаты, где были заложены основы для такого альтернативного рассмотрения. В этих работах было установлено, что при увеличении числа бран в стопке их коллективное гравитационное поле возрастает. В конце концов плита из бран ведёт себя подобно чёрной дыре, но не обычной, а бранообразной, поэтому такая стопка была названа чёрной браной. Как и в случае чёрных дыр, если приблизиться слишком близко к чёрной бране, то вырваться оттуда не получится. И так же как в случае чёрных дыр, если наблюдать издалека за приближением какого-нибудь объекта к чёрной бране, то дошедший до вас свет будет точно так же измотан борьбой с гравитационным притяжением чёрной браны. Это приведёт к тому, что объект будет выглядеть замедляющимся и теряющим энергию.
В этом контексте Малдасена вновь сосредоточился на низкоэнергетических свойствах вселенной, в которой содержится такая чёрная плита. Во многом аналогично тому, как он действовал в первом подходе, он осознал, что в низкоэнергетической физике присутствуют две составляющие, которые можно анализировать независимо друг от друга. Первая — это медленно вибрирующие замкнутые струны, движущиеся в балке пространства, которые являются очевидными переносчиками низкой энергии. Вторая составляющая возникает благодаря присутствию чёрной браны. Представьте теперь, что вы находитесь далеко от чёрной браны и в вашем распоряжении имеется вибрирующая замкнутая струна, энергия которой может быть произвольно большой. Затем представьте, что струна опускается на горизонт событий, а вы наблюдаете за ней с безопасного расстояния. Как говорилось ранее, чёрная брана будет понижать энергию струны; свет, доходящий до вас, будет изображать струну как в замедленном кино. Таким образом, вторыми низкоэнергетическими переносчиками являются любые вибрирующие струны, которые находятся достаточно близко к горизонту событий чёрной браны.
Наконец, Малдасена сравнил оба подхода. Он заметил, что, поскольку они описывают одну и ту же стопку бран, только с разных точек зрения, они обязаны совпадать. Каждое описание вовлекает низкоэнергетические замкнутые струны, движущиеся в балке пространства, поэтому в этой части совпадение очевидно. Однако согласованность должна быть и в остальных частях каждого описания. Удивительно, но именно так и происходит!
Оставшийся кусок первого описания состоит из низкоэнергетических открытых струн, движущихся на три-бранах. Низкоэнергетические струны хорошо описываются квантовой теорией поля точечных частиц, именно то, что нам здесь требуется. Этот тип квантовой теории поля привлекает ряд хитроумных математических построений (чего стоит только одно название — конформно-инвариантная суперсимметричная квантовая калибровочная теория поля), но нам важны две её характеристики, которые можно достаточно легко понять. Во-первых, отсутствие замкнутых струн гарантирует отсутствие гравитационного поля. Во-вторых, поскольку струны движутся только на плотно упакованных в стопку бранах, квантовая теория поля живёт в трёх пространственных измерениях (что в совокупности с одним временным измерением даёт четыре пространственновременных измерения).
Что касается второго описания, то оставшийся кусок состоит из произвольно вибрирующих замкнутых струн, которые, однако, оказались достаточно близко к горизонту событий чёрной браны, а потому кажутся вялыми — то есть как будто они обладают низкой энергией. Такие струны, хотя и ограниченные близостью к чёрной бране, по-прежнему вибрируют и движутся сквозь девять пространственных измерений (что в совокупности с одним временным измерением даёт десять пространственно-временных измерений). Поскольку этот сектор построен из замкнутых струн, в нём присутствует гравитационное взаимодействие.
Исследования Малдасены привели к совершенно невероятному заключению. Квантовая теория поля (определённого вида) точечных частиц без гравитации в четырёх пространственно-временных измерениях (первая точка зрения) описывает такую же физику, что и теория струн с гравитацией, где струны движутся внутри определённой области десятимерного пространства-времени.
В качестве особенно впечатляющего примера рассмотрим задачу, которую исследовал Виттен: как будет выглядеть обычная чёрная дыра, находящаяся внутри вселенной Малдасены, с точки зрения теории на границе. Теория на границе не содержит гравитации, и потому чёрная дыра трансформируется в нечто совсем не похожее. Виттен показал, что ненасытная чёрная дыра является голографической проекцией чего-то совершенно обычного — разгорячённого газа частиц в теории на границе. Подобно настоящей голограмме и порождаемому ею изображению, две теории — чёрная дыра внутри и разогретая квантовая теория поля на границе — ничем друг на друга не похожи, но при этом они несут одинаковую информацию.
В притче Платона о пещере наши чувства воспринимают лишь плоскую, усечённую версию истинной, более богатой реальности. Плоский мир Малдасены совсем другой. Далёкий от какого-либо усечения, он представляет события во всей полноте. Это совершенно другая история, отличная от того, к чему мы привыкли. Но этот плоский мир может вполне оказаться первичным.
Результат Малдасены и многие другие достижения, сделанные за прошедшие годы, воспринимаются как гипотезы. Поскольку математическая структура теории невероятно сложна, нахождение окончательных аргументов является трудной задачей. Однако голографические идеи с успехом прошли строгие математические проверки, попав в главный поток физических исследований, направленных на поиск глубинных основ законов природы.
На этом серия статей-конспектов, посвященных книге «Скрытая реальность: Параллельные миры и глубинные законы Космоса», закончена. Было затронуто немало тем, но это далеко не все, о чем рассказывается в книге. Поэтому, если заинтересовал материал советую самому прочесть книгу.


