Изначально от теории представлений отказались. Сегодня она играет важнейшую роль в большинстве областей математики.

Когда в конце XIX века впервые появилась теория представлений, многие математики сомневались в ценности этого подхода. В 1897 году английский математик Уильям Бёрнсайд писал, что сомневается в том, что эта необычная перспектива даст какие-то полезные результаты.
«Бёрнсайд, по сути, говорил о том, что теория представлений бесполезна», — сказал Джорди Уильямсон из Сиднейского университета в лекции 2015 года.
Прошло более ста лет после её дебюта, и теория представлений стала ключевым ингредиентом во множестве важнейших математических открытий. Однако её ценность сложно оценить с первого раза.
«Не сразу становится понятно, что её стоит изучать», — сказала Эмили Нортон из Кайзерслаутернского технического университета в Германии.
Теория представлений – это способ взять сложные объекты и «представить» их при помощи более простых. В роли сложных объектов часто выступают коллекции из математических объектов – числа или симметрии – находящиеся в определённых структурных отношениях друг с другом. Такие коллекции называют группами. Более простые объекты – это массивы чисел под названием матрицы, ключевой элемент линейной алгебры. Если группы – вещь абстрактная, и с ними часто тяжело работать, то матрицы и линейная алгебра – вещь элементарная.
«Математикам, по сути, про матрицы известно уже всё. Это одна из немногих математических тем, в которой мы хорошо и досконально разобрались», — сказал Джаред Вайнштайн из Бостонского университета.
Чтобы понять, как матрицы могут представлять группы, стоит рассматривать каждый объект по очереди.
Возьмём сначала группы. Чтобы упростить пример, возьмём шесть симметрий равностороннего треугольника:
- Две вращательных (на 120° и 240°).
- Три зеркальных (относительно линий, проведённых из каждой вершины через середину противоположной стороны).
- Тождественная симметрия – когда с треугольником ничего не происходит.

Шесть этих симметрий образуют замкнутую вселенную элементов – группу – формально именуемую S3. Это группа, поскольку любое количество этих симметрий можно применить к треугольнику последовательно и в любом порядке, а итоговый результат будет таким же, как если бы вы применили только одну. К примеру, если отразить треугольник, а потом повернуть его на 120°, то вершины переориентируются таким же образом, как если бы вы применили другое отражение.
«Делаю что-то одно, потом делаю что-то другое. Важно то, что в итоге получается всё равно симметрия треугольника», — сказал Нортон.
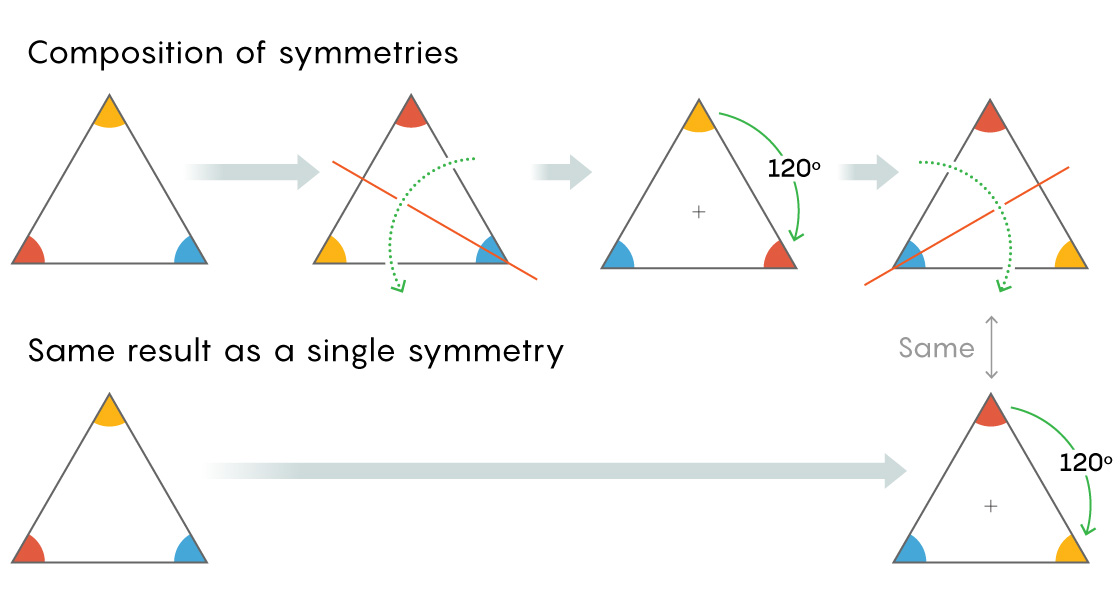
Математики называют комбинацию из двух симметрий композицией. Одно действие из группы (отражение) соединяется с другим (вращение) и даёт третье (другое отражение). Вслед за математиками композицию можно считать умножением.
«Нам нравится считать наши операции умножением, хотя это не перемножение чисел, а умножение преобразований», — сказал Нортон.
Это легко увидеть, если рассмотреть ненулевые вещественные числа, также формирующие группу. У вещественных чисел есть нейтральный элемент– число 1. Любое вещественное число, если его скомбинировать с 1, то есть, умножить на неё, остаётся неизменным. Также можно перемножать любую комбинацию вещественных чисел в любом порядке, и результат тоже всегда будет вещественным числом. Математики говорят, что группа вещественных чисел замкнута относительно умножения, то есть, из группы нельзя выйти, просто перемножая её элементы.
С момента открытия групп в 1830-х, они стали одним из наиболее важных объектов математики. Они кодируют информацию о простых числах, геометрических пространствах и вообще почти всего, что интересует математиков. Решение важной задачи часто превращается в изучение связанной с ней группы. Однако большинство групп гораздо сложнее понять, чем группу симметрий равностороннего треугольника. В группы Ли, к примеру, входит не шесть элементов, а бесконечное количество.
«Иногда группы становятся чересчур сложными», — сказал Вайнштейн.
И это подводит нас к теории представлений, превращающей загадочный периодами мир групп в хорошо известную нам территорию линейной алгебры.
Линейная алгебра изучает простейшие преобразования над объектами, известными, как векторы – по сути, направленными отрезками. Эти объекты определяются координатами, которые можно записать в виде матрицы – массива объектов.
Преобразование происходит при применении к вектору другой матрицы. К примеру, когда мы применяем к вектору матрицу
[2 0] [0 2]То он вытягивается в длину в два раза. Это пример линейного преобразования.
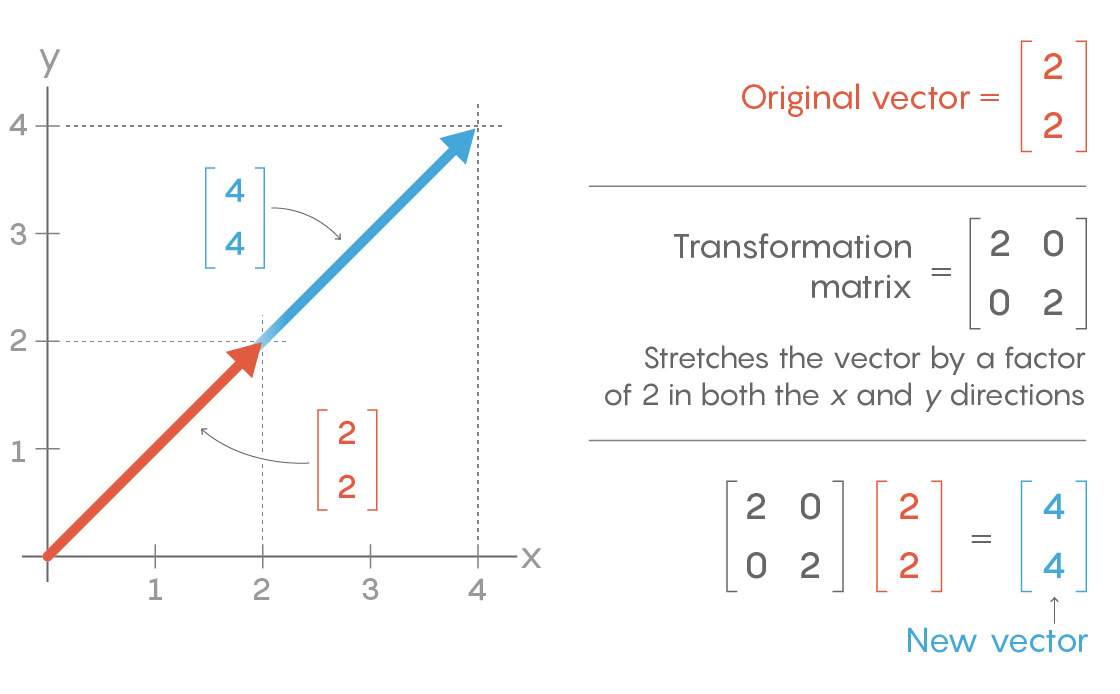
Другие матрицы выполняют другие линейные преобразования – отражения, повороты и сдвиги. Есть и нейтральная матрица, оставляющая вектор без изменений (точно так же, как тождественная симметрия оставляет треугольник неизменным, а число 1 оставляет неизменными другие числа).
[1 0] [0 1]Линейная алгебра определяет арифметику, стоящую за этими преобразованиями. Матрицы можно перемножать, складывать и вычитать так же легко, как мы проделываем это с числами.
Теория представлений создаёт мост между теорией групп и линейной алгеброй, назначая матрицу каждому элементу группы по определённым правилам. К примеру, нейтральному элементы группы нужно сопоставить нейтральную матрицу. Также эти назначения должны сохранять взаимоотношения элементов группы. Если отражение, умноженное на определённый поворот, равняется другому отражению, тогда матрица, сопоставленная первому отражению, умноженная на матрицу, сопоставленную повороту, должна равняться матрице, сопоставленной второму отражению. Набор матриц, удовлетворяющих этим требованиям, называется представлением группы.
Представление даёт упрощённую картину группы, так же, как чёрно-белая фотография может служить недорогой имитацией оригинального цветного изображения. Можно сказать, что оно «помнит» некоторую базовую, но необходимую информацию о группе, забывая всё остальное. Математики стремятся избегать необходимости иметь дело со всеми сложностями группы; вместо этого они получают представление о её свойствах, изучая то, как она ведёт себя при превращении в упрощённый формат линейных преобразований.
«Нам не нужно пытаться объятью всю группу сразу, — сказал Нортон. – Мы можем изучать её представление, меньшее по размеру, и всё равно что-то понять по поводу этой группы».
Почти всегда группу можно представить несколькими способами. К примеру, у S3 есть три разных представления через матрицы вещественных чисел: тривиальное, отражённое и знаковое.
Математики расставляют представления заданной группы в таблице — таблице характеров – где суммируется информация о группе. Строки обозначают каждое из различных представлений, а столбцы относятся к важным матрицам этих представлений – матрице, сопоставленной нейтральному элементу группы, и матрицам, сопоставленным «генерирующим» элементам, порождающим все остальные элементы. Элементами таблицы служат значения, которые называют «следами» матриц, и подсчитывают через сумму диагональных элементов от левого верхнего угла к правому нижнему. Ниже приводится таблица характеров для трёх представлений S3.
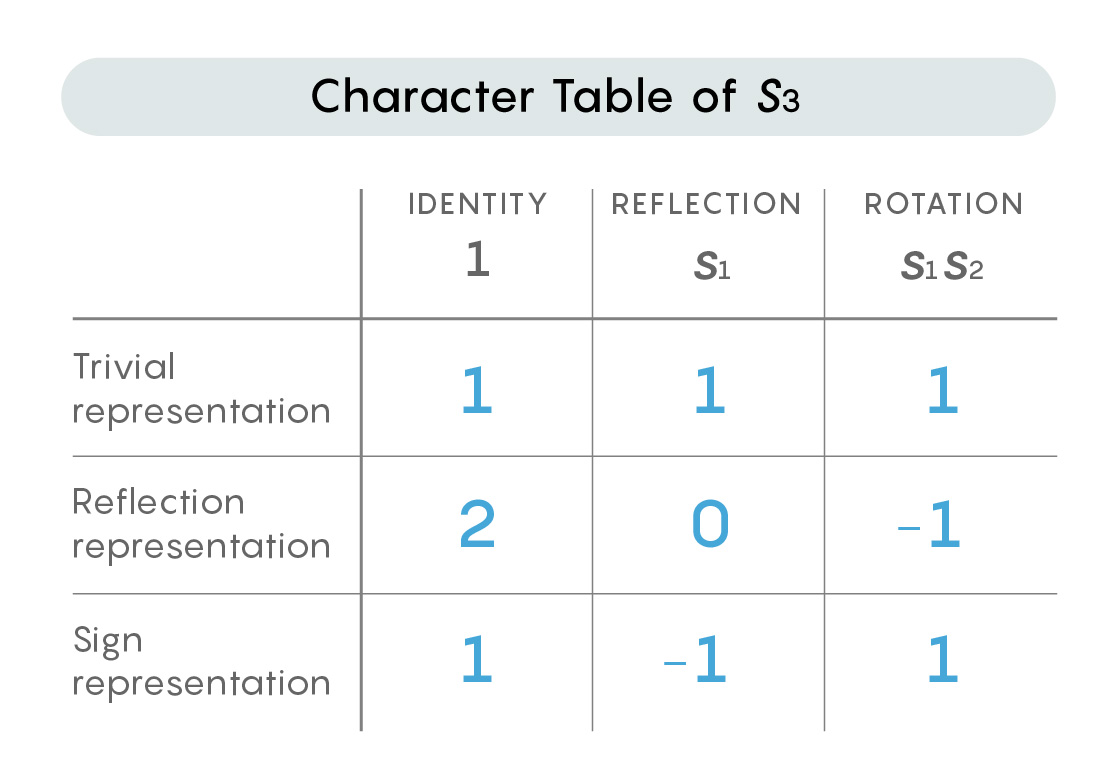
Таблица характеров даёт упрощённую картину группы. Каждое из входящих в неё представлений даёт свою, отличающуюся от других информацию. Математики комбинируют различные перспективы, которые дают им эти представления, и получают общее впечатление о группе.
«Много разных представлений помнят разные вещи, и если собрать всё это вместе, получится такая калейдоскопическая картинка вашей группы», — сказал Нортон.
В приведённой выше таблице характеров математики сразу же узнают таблицу для S3. Однако иногда одна и та же таблица характеров может представлять разные группы – при работе с упрощениями некая неоднозначность всегда возникает.
В таких неоднозначных случаях математики могут пользоваться дополнительными инструментами. Один из них – изменение числовой системы, в рамках которой они создают своё представление. Вышеуказанное представление S3 получается при помощи матриц с вещественными числами в качестве элементов – однако можно было бы использовать и комплексные числа (такие, у которых есть реальная и мнимая часть). Большая часть теории представлений их и использует.
Некоторые из самых продуктивных представлений не используют ни вещественные, ни комплексные числа. Они используют матрицы, элементы которых взяты из миниатюрных, или модульных числовых систем. Это мир «арифметики циферблата», в котором 7+6 оборачивается вокруг 12-часового циферблата и даёт 1. У двух групп с одинаковыми таблицами характеров в вещественном представлении могут быть разные таблицы характеров в модульном представлении, что позволяет различать их.
Сегодня теория представлений является основным инструментом для множества областей математики: алгебры, топологии, геометрии, математической физики и теории чисел – включая обширную программу Ленглендса.
«Философия теории представлений начала с огромной скоростью поглощать огромные области математики во второй половине XX века», — сказал мне Уильямсон.
Теория представлений – и в частности, модульные представления – сыграли важную роль в знаковом доказательстве Великой теоремы Ферма, полученном Эндрю Уайлсом в 1994 году. В задаче вставал вопрос о существовании решений уравнений вида an + bn = cn в целых числах. Уайлс доказал, что для n>2 таких решений не существует. Если говорить примерно, то он доказывал, что если бы такие решения существовали, привели бы к появлению группы «эллиптической кривой» с весьма необычными свойствами. Эти свойства были настолько необычными, что казалось возможным доказать невозможность существования подобного объекта. Однако напрямую доказать, что он не существует, оказалось слишком тяжело. Вместо этого Уайлс обратился к семейству модульных представлений, которое было бы связано с этой группой, если бы она существовала. Он доказал, что такого семейства модульных представлений быть не может, что означает, что не может существовать и группы (или эллиптической кривой), что означает, что и решений тоже не существует.
Что, в свою очередь, означает, что примерно через 100 лет после того, как Уильям Бёрнсайд отбросил теорию представлений как бесполезную, она оказалась критически важным компонентом, возможно, наиболее знаменитого доказательства XX века.
«Я не мог придумать доказательства Великой теоремы Ферма, в котором бы нигде не использовалась теория представлений », — сказал Вайнштейн.


