Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Supersolid formation in a quantum gas breaking a continuous translational symmetry

Nature volume 543, pages 87–90 (2017)Cite this article

Subjects

Abstract

The concept of a supersolid state combines the crystallization of a many-body system with dissipationless flow of the atoms from which it is built. This quantum phase requires the breaking of two continuous symmetries: the phase invariance of a superfluid and the continuous translational invariance to form the crystal1,2. Despite having been proposed for helium almost 50 years ago3,4, experimental verification of supersolidity remains elusive5,6. A variant with only discrete translational symmetry breaking on a preimposed lattice structure—the ‘lattice supersolid’7—has been realized, based on self-organization of a Bose–Einstein condensate8,9. However, lattice supersolids do not feature the continuous ground-state degeneracy that characterizes the supersolid state as originally proposed. Here we report the realization of a supersolid with continuous translational symmetry breaking along one direction in a quantum gas. The continuous symmetry that is broken emerges from two discrete spatial symmetries by symmetrically coupling a Bose–Einstein condensate to the modes of two optical cavities. We establish the phase coherence of the supersolid and find a high ground-state degeneracy by measuring the crystal position over many realizations through the light fields that leak from the cavities. These light fields are also used to monitor the position fluctuations in real time. Our concept provides a route to creating and studying glassy many-body systems with controllably lifted ground-state degeneracies, such as supersolids in the presence of disorder.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Breaking continuous translational symmetry in a superfluid quantum gas.
Figure 2: Self-organized phases in the two-cavity system.
Figure 3: Emergence of a doubly self-organized phase.
Figure 4: Breaking continuous translational symmetry.

Similar content being viewed by others

References

  1. Boninsegni, M. & Prokof’ev, N. V. Supersolids: what and where are they? Rev. Mod. Phys. 84, 759–776 (2012)

    Article  CAS  ADS  Google Scholar 

  2. Chan, M. H. W., Hallock, R. B. & Reatto, L. Overview on solid 4He and the issue of supersolidity. J. Low Temp. Phys. 172, 317–363 (2013)

    Article  CAS  ADS  Google Scholar 

  3. Andreev, A. F. & Lifshitz, I. M. Quantum theory of defects in crystals. Sov. Phys. JETP 29, 1107–1113 (1969)

    ADS  Google Scholar 

  4. Thouless, D. J. The flow of a dense superfluid. Ann. Phys. 52, 403–427 (1969)

    Article  ADS  Google Scholar 

  5. Kim, E. & Chan, M. H. W. Probable observation of a supersolid helium phase. Nature 427, 225–227 (2004)

    Article  CAS  ADS  Google Scholar 

  6. Kim, D. Y. & Chan, M. H. W. Absence of supersolidity in solid helium in porous Vycor glass. Phys. Rev. Lett. 109, 155301 (2012)

    Article  ADS  Google Scholar 

  7. Matsuda, H. & Tsuneto, T. Off-diagonal long-range order in solids. Prog. Theor. Phys. 46, 411–436 (1970)

    Article  Google Scholar 

  8. Baumann, K., Guerlin, C., Brennecke, F. & Esslinger, T. Dicke quantum phase transition with a superfluid gas in an optical cavity. Nature 464, 1301–1306 (2010)

    Article  CAS  ADS  Google Scholar 

  9. Mottl, R. et al. Roton-type mode softening in a quantum gas with cavity-mediated long-range interactions. Science 336, 1570–1573 (2012)

    Article  CAS  ADS  Google Scholar 

  10. Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008)

    Article  CAS  ADS  Google Scholar 

  11. Lahaye, T., Menotti, C., Santos, L., Lewenstein, M. & Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 72, 126401 (2009)

    Article  ADS  Google Scholar 

  12. Kadau, H. et al. Observing the Rosensweig instability of a quantum ferrofluid. Nature 530, 194–197 (2016)

    Article  CAS  ADS  Google Scholar 

  13. Zeiher, J. et al. Many-body interferometry of a Rydberg-dressed spin lattice. Nat. Phys. 12, 1095–1099 (2016)

    Article  CAS  Google Scholar 

  14. Moses, S. A. et al. Creation of a low-entropy quantum gas of polar molecules in an optical lattice. Science 350, 659–662 (2015)

    Article  CAS  ADS  Google Scholar 

  15. Goldman, N., Juzeliūnas, G., Öhberg, P. & Spielman, I. B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 77, 126401 (2014)

    Article  CAS  ADS  Google Scholar 

  16. Li, J. et al. Spin-orbit coupling and spin textures in optical superlattices. Phys. Rev. Lett. 117, 185301 (2016)

    Article  ADS  Google Scholar 

  17. Ostermann, S., Piazza, F. & Ritsch, H. Spontaneous crystallization of light and ultracold atoms. Phys. Rev. X 6, 021026 (2016)

    Google Scholar 

  18. Gopalakrishnan, S., Lev, B. L. & Goldbart, P. M. Emergent crystallinity and frustration with Bose–Einstein condensates in multimode cavities. Nat. Phys. 5, 845–850 (2009)

    Article  CAS  Google Scholar 

  19. Labeyrie, G. et al. Optomechanical self-structuring in a cold atomic gas. Nat. Photon. 8, 321–325 (2014)

    Article  CAS  ADS  Google Scholar 

  20. Kollár, A. J. et al. Supermode-density-wave-polariton condensation. Preprint at https://arxiv.org/abs/1606.04127 (2016)

  21. Lemoine, M., Martin, J. & Peter, P. (eds) Inflationary Cosmology Ch. 11 (Springer, 2008)

  22. Eichhorn, A., Mesterházy, D. & Scherer, M. M. Multicritical behavior in models with two competing order parameters. Phys. Rev. E 88, 042141 (2013)

    Article  ADS  Google Scholar 

  23. Ritsch, H., Domokos, P., Brennecke, F. & Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. Rev. Mod. Phys. 85, 553–601 (2013)

    Article  CAS  ADS  Google Scholar 

  24. Asbóth, J. K., Domokos, P. & Ritsch, H. Correlated motion of two atoms trapped in a single-mode cavity field. Phys. Rev. A 70, 013414 (2004)

    Article  ADS  Google Scholar 

  25. Safaei, S., Miniatura, C. & Grémaud, B. Triangular and honeycomb lattices of cold atoms in optical cavities. Phys. Rev. A 92, 043810 (2015)

    Article  ADS  Google Scholar 

  26. Nagy, D., Szirmai, G. & Domokos, P. Critical exponent of a quantum-noise-driven phase transition: the open-system Dicke model. Phys. Rev. A 84, 043637 (2011)

    Article  ADS  Google Scholar 

  27. Brennecke, F. et al. Real-time observation of fluctuations at the driven-dissipative Dicke phase transition. Proc. Natl Acad. Sci. USA 110, 11763–11767 (2013)

    Article  CAS  ADS  Google Scholar 

  28. Strack, P. & Sachdev, S. Dicke quantum spin glass of atoms and photons. Phys. Rev. Lett. 107, 277202 (2011)

    Article  Google Scholar 

  29. Fan, J. et al. Hidden continuous symmetry and Nambu-Goldstone mode in a two-mode Dicke model. Phys. Rev. A 89, 023812 (2014)

    Article  ADS  Google Scholar 

  30. Baksic, A. & Ciuti, C. Controlling discrete and continuous symmetries in “superradiant” phase transitions with circuit QED systems. Phys. Rev. Lett. 112, 173601 (2014)

    Article  ADS  Google Scholar 

  31. Léonard, J. et al. Optical transport of ultracold atoms using focus-tunable lenses. New J. Phys. 16, 093028 (2014)

    Article  ADS  Google Scholar 

  32. Emary, C. & Brandes, T. Chaos and the quantum phase transition in the Dicke model. Phys. Rev. E 67, 066203 (2003)

    Article  MathSciNet  ADS  Google Scholar 

  33. Hayn, M., Emary, C. & Brandes, T. Phase transitions and dark-state physics in two-color superradiance. Phys. Rev. A 84, 053856 (2011)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank E. Demler, J. Larson and B. P. Venkatesh for discussions on U(1) symmetries in optical cavities and M. Lee for contributions in the building stage of the experimental apparatus. We acknowledge funding from Synthetic Quantum Many-Body Systems (European Research Council advanced grant) and the EU Collaborative Project TherMiQ (Grant Agreement 618074), and also SBFI support for Horizon2020 project QUIC and SNF support for NCCR QSIT and DACH project ‘Quantum Crystals of Matter and Light’.

Author information

Authors and Affiliations

  1. Institute for Quantum Electronics, ETH Zurich, Zurich, 8093, Switzerland

    Julian Léonard, Andrea Morales, Philip Zupancic, Tilman Esslinger & Tobias Donner

Authors
  1. Julian Léonard
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Andrea Morales
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Philip Zupancic
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Tilman Esslinger
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Tobias Donner
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All authors contributed extensively to the work presented here.

Corresponding author

Correspondence to Tilman Esslinger.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Additional information

Reviewer Information Nature thanks K. Hazzard and D. Huse for their contribution to the peer review of this work.

Extended data figures and tables

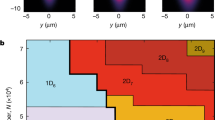
Extended Data Figure 1 Mean-field solution of the phase diagram.

Order parameters α1 and α2 as a function of the pump–cavity detunings Δ1 and Δ2. The Raman coupling λ is fixed by the experimental value of the transverse pump lattice depth of 38ħωrec. The mean-field model includes cavity decay, different vacuum Rabi frequencies gi and the transverse pump potential.

Source data

Extended Data Figure 2 Lattice geometries for different choices of the phase ϕ of the transverse pump field for balanced cavity fields.

The atoms are cut into one-dimensional lines by the strong transverse pump field. On top, spatial distributions between triangular (ϕ = 0) and hexagonal (ϕ = π/2) can form through the interference between the cavity light fields and the transverse pump, depending on the phase ϕ of the latter.

Extended Data Figure 3 Dependence of the lattice structure on the cavity field amplitudes.

The ground-state manifold for equal couplings and detunings in is a circle in the space of the cavity fields α1 and α2. For each combination of fields, the interference potential in equation (3) between the transverse pump and cavity fields for ϕ = π/2 will have its minima at different positions. Following the circle clockwise, every second line moves left (top highlighted line) while the others move right (bottom highlighted line).

Extended Data Figure 4 Transition between discrete and continuous symmetries.

a–c, Histograms (normalized to unity area) of the angles θ describing the position of the crystal lattice, measured in the same way as the data in Fig. 4, but at Δ1 = −2.1 MHz (a), Δ1 = −2.2 MHz (b) and Δ1 = −2.3 MHz (c). The grey lines show kernel density estimation analyses with a Gaussian kernel, whose bandwidth of 0.13π/2 was determined from a cross-validation maximum likelihood reconstruction. Each histogram consists of 19–49 realizations.

Source data

PowerPoint slides

Source data

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Léonard, J., Morales, A., Zupancic, P. et al. Supersolid formation in a quantum gas breaking a continuous translational symmetry. Nature 543, 87–90 (2017). https://doi.org/10.1038/nature21067

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature21067

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing