Ныряем вглубь: от CSS до транзистора

Мы на этих шагах останавливаться подробно не будем. После них наступает собственно отрисовка нужных элементов.

За отрисовку границ отвечает файл nsCSSRenderingBorders.cpp. А общая функция отрисовки границ называется (кто бы мог подумать): DrawBorders(). Функция выбирает оптимальный способ отрисовки для различных ситуаций. У нас относительно простой случай: есть border-radius, но границы со всех сторон сплошные (solid) и одного цвета.

if (allBordersSame &&       mCompositeColors[0] == nullptr &&       mBorderStyles[0] == NS_STYLE_BORDER_STYLE_SOLID &&       !mAvoidStroke &&       !mNoBorderRadius)   {     // Relatively simple case.     gfxRect outerRect = ThebesRect(mOuterRect);     RoundedRect borderInnerRect(outerRect, mBorderRadii);     borderInnerRect.Deflate(mBorderWidths[eSideTop],                             mBorderWidths[eSideBottom],                             mBorderWidths[eSideLeft],                             mBorderWidths[eSideRight]);      // Instead of stroking we just use two paths: an inner and an outer.     // This allows us to draw borders that we couldn't when stroking. For example,     // borders with a border width >= the border radius. (i.e. when there are     // square corners on the inside)     //     // Further, this approach can be more efficient because the backend     // doesn't need to compute an offset curve to stroke the path. We know that     // the rounded parts are elipses we can offset exactly and can just compute     // a new cubic approximation.     RefPtr builder = mDrawTarget->CreatePathBuilder();     AppendRoundedRectToPath(builder, mOuterRect, mBorderRadii, true);     AppendRoundedRectToPath(builder, ToRect(borderInnerRect.rect), borderInnerRect.corners, false);     RefPtr path = builder->Finish();     mDrawTarget->Fill(path, color);     return;   } 

Есть гораздо более сложные варианты, например стыковка в углах с border-radius разных типов границ dotted и dashed, см. DrawDashedOrDottedCorner(). Там в коде совершенно

    //      radius.width     // |<----------------->|     // |                   |     // |             ___---+-------------     // |         __--     #|#       ###     // |       _-        ##|##     #####     // |     /           ##+##     ##+##     // |   /             # P #     #####     // |  |               #|#       ###     // | |             __--+-------------     // ||            _-    ^     // ||          /       |     // |         /        first dot is filled     // |        |     // |       |     // |      |     // |      |     // |      |     // +------+     // |##  ##|     // |##  ##|     // |##  ##| 

Но вернемся к нашему if. Из комментария мы узнаем, что в данном случае граница рисуется с помощью двух прямоугольников — внутреннего и внешнего, затем созданный контур (path) заливается нужным цветом.

AppendRoundedRectToPath(builder, mOuterRect, mBorderRadii, true); AppendRoundedRectToPath(builder, ToRect(borderInnerRect.rect), borderInnerRect.corners, false); RefPtr path = builder->Finish(); mDrawTarget->Fill(path, color);

Идем в AppendRoundedRectToPath() в gfx/2d/PathHelpers.cpp.

Опять расставляем брейкпоинты

Из комментария к функции узнаем, что уголки отрисовываются по четырем контрольным точкам кривыми Безье. Кривые Безье часто применяются в компьютерной графике, в том числе и для отрисовки дуг кругов и эллипсов. Как мы дальше узнаем из комментария, существует множество вариантов выбора контрольных точек для построения кривой. При этом нам необходимо, чтобы точки 0 и 3 принадлежали сторонам прямоугольника, точки 0, 1 и C лежали на одной прямой, точки 3, 2 и C — на другой. См. рисунок:

Нам остается рассчитать соотношения длин отрезков 01/0C и 32/3С. Тут авторы используют приближенные вычисления и получают магическую константу альфа:

const Float alpha = Float(0.55191497064665766025);

К сожалению, статьи с алгоритмом выбора контрольных точек, на которую ссылается комментарий, нет в открытом доступе. Но вообще нужно отметить, что в компьютерной графике алгоритмы часто используют апроксимацию для повышения производительности. Например, Алгоритм Брезенхема позволяет рисовать отрезки и окружности не «в лоб» — решением уравнений y = f(x), а более хитрыми целочисленными операциями. Тоже самое с заливкой и т.д.

Далее в цикле мы идем от угла к углу, с помощью alpha вычисляем координаты контрольных точек и, наконец, вызываем функции отрисовки линии границы и дуги угла:

aPathBuilder->LineTo(p0); aPathBuilder->BezierTo(p1, p2, p3); 

void AppendRoundedRectToPath(PathBuilder* aPathBuilder,                         const Rect& aRect,                         const RectCornerRadii& aRadii,                         bool aDrawClockwise) {   // For CW drawing, this looks like:   //   //  ...******0**      1    C   //              ****   //                  ***    2   //                     **   //                       *   //                        *   //                         3   //                         *   //                         *   //   // Where 0, 1, 2, 3 are the control points of the Bezier curve for   // the corner, and C is the actual corner point.   //   // At the start of the loop, the current point is assumed to be   // the point adjacent to the top left corner on the top   // horizontal.  Note that corner indices start at the top left and   // continue clockwise, whereas in our loop i = 0 refers to the top   // right corner.   //   // When going CCW, the control points are swapped, and the first   // corner that's drawn is the top left (along with the top segment).   //   // There is considerable latitude in how one chooses the four   // control points for a Bezier curve approximation to an ellipse.   // For the overall path to be continuous and show no corner at the   // endpoints of the arc, points 0 and 3 must be at the ends of the   // straight segments of the rectangle; points 0, 1, and C must be   // collinear; and points 3, 2, and C must also be collinear.  This   // leaves only two free parameters: the ratio of the line segments   // 01 and 0C, and the ratio of the line segments 32 and 3C.  See   // the following papers for extensive discussion of how to choose   // these ratios:   //   //   Dokken, Tor, et al. "Good approximation of circles by   //      curvature-continuous Bezier curves."  Computer-Aided   //      Geometric Design 7(1990) 33--41.   //   Goldapp, Michael. "Approximation of circular arcs by cubic   //      polynomials." Computer-Aided Geometric Design 8(1991) 227--238.   //   Maisonobe, Luc. "Drawing an elliptical arc using polylines,   //      quadratic, or cubic Bezier curves."   //      http://www.spaceroots.org/documents/ellipse/elliptical-arc.pdf   //   // We follow the approach in section 2 of Goldapp (least-error,   // Hermite-type approximation) and make both ratios equal to   //   //          2   2 + n - sqrt(2n + 28)   //  alpha = - * ---------------------   //          3           n - 4   //   // where n = 3( cbrt(sqrt(2)+1) - cbrt(sqrt(2)-1) ).   //   // This is the result of Goldapp's equation (10b) when the angle   // swept out by the arc is pi/2, and the parameter "a-bar" is the   // expression given immediately below equation (21).   //   // Using this value, the maximum radial error for a circle, as a   // fraction of the radius, is on the order of 0.2 x 10^-3.   // Neither Dokken nor Goldapp discusses error for a general   // ellipse; Maisonobe does, but his choice of control points   // follows different constraints, and Goldapp's expression for   // 'alpha' gives much smaller radial error, even for very flat   // ellipses, than Maisonobe's equivalent.   //   // For the various corners and for each axis, the sign of this   // constant changes, or it might be 0 -- it's multiplied by the   // appropriate multiplier from the list before using.    const Float alpha = Float(0.55191497064665766025);    typedef struct { Float a, b; } twoFloats;    twoFloats cwCornerMults[4] = { { -1,  0 },    // cc == clockwise                                  {  0, -1 },                                  { +1,  0 },                                  {  0, +1 } };   twoFloats ccwCornerMults[4] = { { +1,  0 },   // ccw == counter-clockwise                                   {  0, -1 },                                   { -1,  0 },                                   {  0, +1 } };    twoFloats *cornerMults = aDrawClockwise ? cwCornerMults : ccwCornerMults;    Point cornerCoords[] = { aRect.TopLeft(), aRect.TopRight(),                            aRect.BottomRight(), aRect.BottomLeft() };    Point pc, p0, p1, p2, p3;    if (aDrawClockwise) {     aPathBuilder->MoveTo(Point(aRect.X() + aRadii[RectCorner::TopLeft].width,                                aRect.Y()));   } else {     aPathBuilder->MoveTo(Point(aRect.X() + aRect.Width() - aRadii[RectCorner::TopRight].width,                                aRect.Y()));   }    for (int i = 0; i < 4; ++i) {     // the corner index -- either 1 2 3 0 (cw) or 0 3 2 1 (ccw)     int c = aDrawClockwise ? ((i+1) % 4) : ((4-i) % 4);      // i+2 and i+3 respectively.  These are used to index into the corner     // multiplier table, and were deduced by calculating out the long form     // of each corner and finding a pattern in the signs and values.     int i2 = (i+2) % 4;     int i3 = (i+3) % 4;      pc = cornerCoords[c];      if (aRadii[c].width > 0.0 && aRadii[c].height > 0.0) {       p0.x = pc.x + cornerMults[i].a * aRadii[c].width;       p0.y = pc.y + cornerMults[i].b * aRadii[c].height;        p3.x = pc.x + cornerMults[i3].a * aRadii[c].width;       p3.y = pc.y + cornerMults[i3].b * aRadii[c].height;        p1.x = p0.x + alpha * cornerMults[i2].a * aRadii[c].width;       p1.y = p0.y + alpha * cornerMults[i2].b * aRadii[c].height;        p2.x = p3.x - alpha * cornerMults[i3].a * aRadii[c].width;       p2.y = p3.y - alpha * cornerMults[i3].b * aRadii[c].height;        aPathBuilder->LineTo(p0);       aPathBuilder->BezierTo(p1, p2, p3);     } else {       aPathBuilder->LineTo(pc);     }   }    aPathBuilder->Close(); } 

А вот дальше все зависит от бекенда 2D графики, который использует Mozilla.

Графический движок

Gecko использует платформонезависимую библиотеку Moz2D, которая в свою очередь может использовать один из бекендов: Cairo, Skia, Direct2D, Quartz и NV Path. Например, для Windows доступны Direct2D, Cairo, Skia. Skia является также бекендом Chromium. Поменять бекенд можно в about:config. Бекенды, в свою очередь, могут считать все на CPU, а могут использовать в какой-то мере аппаратное ускорение GPU. Например, у Skia есть свой OpenGL бекенд — Ganesh.

Код Direct2D закрыт, поэтому лучше включим Skia и посмотрим, что она делает. Вызывается функция отрисовки кубической кривой SkPath::cubicTo. Чтобы построить кривую она разбивается алгоритмом де Кастельжо на некоторое число прямых отрезков, которые собственно и отрисовываются (см. core/SkGeometry.cpp).

Машинный код

У меня, если честно, не получилось до конца разобраться во внутренностях Skia, поэтому я сделал шаг назад — к AppendRoundedRectToPath(), где все операции происходят над целыми числами — что может быть проще?
Открыв дизассемблированный код, мы должны найти в нем операцию сложения.

... 142B1863 00 00                add         byte ptr [eax],al   142B1865 00 8D 43 FF 0F 84    add         byte ptr [ebp-7BF000BDh],cl   142B186B 67 01 00             add         dword ptr [bx+si],eax   142B186E 00 99 0F 57 C9 F7    add         byte ptr [ecx-836A8F1h],bl   142B1874 F9                   stc   142B1875 8B C3                mov         eax,ebx   142B1877 8B CA                mov         ecx,edx   142B1879 99                   cdq   142B187A F7 7C 24 28          idiv        eax,dword ptr [esp+28h]   ... 

Ага! Даже такой далекий от ASM человек, как я, легко догадается, что за сложение отвечает операция ADD. Возьмем первую операцию:
142B1863 00 00 add byte ptr [eax],al
0x142B1863 — адрес в оперативной памяти
0x00 — opcode — код инструкции процессора. Эта Mozilla скомпилирована под х86, и, открыв таблицу инструкций х86, мы увидим, что код 00 означает 8-битную операцию сложения с мнемоникой ADD. Первым операндом может быть регистр или ячейка оперативной памяти, вторым — регистр. Первый операнд складывается со вторым, результат записывается в первый. Поясню, на всякий случай, что регистр — это сверхбыстрая оперативная память внутри процессора, например для хранения промежуточных результатов вычислений.
Второй байт тоже равен 0x00 и называется MOD-REG-R/M. Его биты задают операнды и способ адресации.

MOD = 00b в комбинации с R/M = 000b означает, что используется косвенная адресация
REG = 000b означает, что используется регистр AL (младшие 8-бит регистра EAX)[eax] — указывает на то, что сложение производится с ячейкой оперативной памяти, адрес которой лежит в регистре EAX

Как же процессор обрабатывает команду ADD?

Процессор

По описанию микроархитектуры Skylake я составил (крайне упрощенный) перечень этапов:

1. Инструкции x86 выбираются из кэша инструкций L1 32Кб в буффер предекодирования блоками по 16 байт
2. Предекодированные команды организуются в очередь Instruction Queue (размером 2х25) и попадают в декодеры
3. Декодер преобразует x86 операцию в 1-4 машинные микрооперации (µOPs). Наша ADD станет 1 µOP для ALU (арифметическо-логическое устройство) и 2 µOP для AGU (устройство вычисления адреса) (см., но это не точно). В целях оптимизации процессор на этом этапе может сливать две х86 инструкции или две микрооперации в одну.
4. Микрооперации попадают в Allocation Queue (IDQ). Здесь тоже применяются оптимизации, такие как Loop Stream Detector — отключение выборки при обнаружении цикла.
5. Начинается исполнение: микрооперация попадает в буфер переупорядочения, где оптимизируется порядок будущего исполнения операций. Для ускорения выполнения свободные физические регистры процессора временно переименовываются в нужные для исполнения операции. Производятся другие оптимизации.
6. Микрооперация попадает в диспетчер Unified Scheduler, который решает в какой момент и в какой порт отправить операции для исполнения вне очередности их поступления. За каждым портом располагается исполнительное устройство. Наши микрооперации попадут в ALU и AGU.

Ядро SkyLake. Изображение с сайта en.wikichip.org.

Повторюсь, это моё очень упрощенное описание и не претендует на точность и полноту. Для дальнейшего ознакомления рекомендую к прочтению пост Путешествие через вычислительный конвейер процессора и статья Процессоры семейства Intel Core i7

АЛУ

Теперь интересно было бы узнать, что происходит в ALU: каким образом складываются числа? К сожалению, информация по конкретной реализации микроархитектуры и АЛУ является коммерческой тайной Intel, поэтому далее обратимся к теории.

Устройство для сложения двух двоичных разрядов (т.е. бит) называется сумматором. На выходе получается сумма и бит переноса.

Источник: Википедия

Т.к. в реальной жизни нам нужно складывать числа, состоящие из нескольких разрядов, сумматор должен принимать на вход еще и бит переноса от предыдущего разряда. Такой сумматор называется полным.

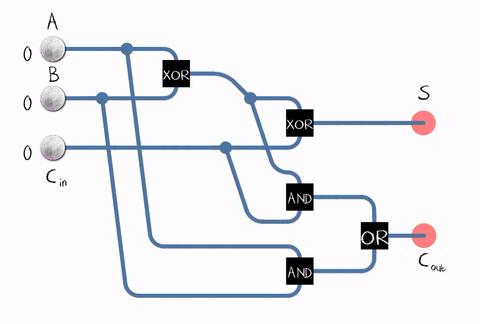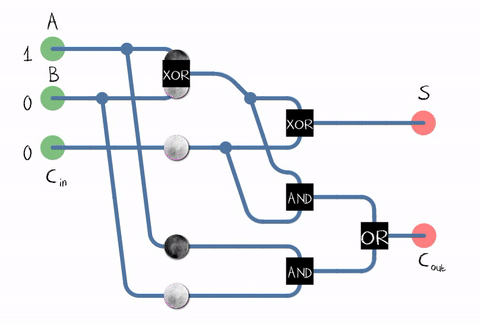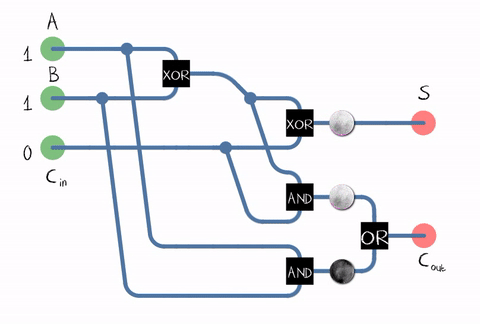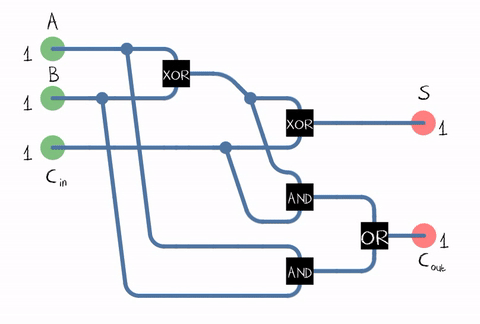
Источник: Википедия

Как видно из рисунка, сумматор составляется из логических элементов: XOR, AND, OR. А каждый логический элемент может быть реализован с помощью нескольких транзисторов. Или даже реле.

Пример реализации полного сумматора на КМОП-транзисторах. Источник

Вот мы и добрались до транзистора! Хотя, конечно, на транзисторах работает не только ALU, но и другие блоки процессора, а больше всего транзисторов используется в кэш-памяти в качестве её ячеек.

В реальности схема сумматора в нашем процессоре может быть построена по-другому и быть гораздо сложнее. Например, уже Intel 8008 45 лет назад умел вычислять все биты переноса заранее, чтобы выполнять сложение параллельно (т.н. сумматор с параллельным переносом). Кому интересно, почитайте интересный пост о реверс-инжиниринге ALU Intel 8008 в блоге Ken Shirriff. Т.е. используются различные оптимизации: например, умножение тоже выгодно делать не «в лоб».

Выводы: что мы узнали?

• Всё сложно
• Наглядно показано: чтобы решить проблему излишней сложности, инженеры используют разбиение сложных систем на уровни (слои).
• Многоуровневые архитектуры позволяют обеспечить переносимость: например, Firefox может запускаться в различных ОС и на различном оборудовании.
• Взаимодействие между уровнями осуществляется за счет открытости спецификаций на интерфейсы, сервисы и форматы данных, например HTML и CSS, С++, набор команд x86 и т.п.
• В самом низу трудится наш юбиляр — транзистор.

P.S. Т.к. я — дилетант (веб-разработчик), и C++, ASM, архитектуру ВТ знаю совсем чуть-чуть — из институтского курса, я мог что-то и напутать. Пожалуйста, не стесняйтесь присылать замечания.